Kaplan-Meier生存分析(Kaplan-Meier Survival Analysis)——SAS软件实现

关键词：SAS; Kaplan-Meier生存分析; 生存分析; KM生存分析; Log-rank检验; 生存曲线

一、案例介绍

某肿瘤研究中心收集了2010年至2015年确诊为宫颈癌的患者生存数据, 欲探究不同组织学分级的宫颈癌患者的生存结局有无差异，部分数据见图1。本文案例可从“附件下载”处下载。其中， Status表示生存状态(0=“删失”，1=“死亡”)，Time表示宫颈癌患者的生存时间(月)，Hist_stage表示组织学分级。

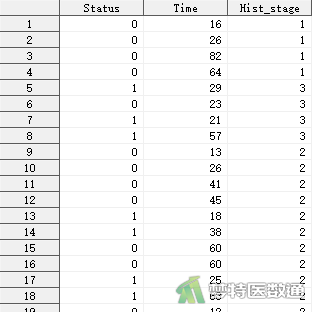
二、问题分析

本案例的分析目的是比较三种组织学等级的宫颈癌患者的生存结局有无差异，可以采用Kaplan-Meier生存分析。但需要满足4个条件：

条件1：结局为互斥的二分类变量，即删失和死亡，本案例数据满足该条件。

条件2：随访时间或生存时间定义明确，并为量化数据，即以天、周、月、年等为单位的具体数值。本案例数据的生存时间为准确可测量的月数，满足该条件。

条件3：不宜有长期变异存在。对于动态队列，研究对象不是同时进入队列的，那么如果后期进入队列的研究对象使用了新的治疗方案和药物，生存率提高，那么整个队列的生存结果就会发生偏倚。该条件需要根据实际情况来判断，这里默认无长期变异。

条件4：删失在各组的分布相似。该条件需要软件分析来判断。

三、软件操作及结果解读

(一) 适用条件判断 (删失事件的占比与分布)

 1. SAS实现

首先导入数据，代码如下：

proc import datafile="G: \KM生存分析1.xlsx" dbms=xlsx out=data1 replace;
run;

使用如下的proc freq过程步，统计不同组织学分级的删失情况：

proc freq data=data1;
	tables status*Hist_stage;
run;

2. 结果解读

如图2所示，3427个患者中，417人发生终点事件，3010人删失。组织学分级为1级的患者中2266 (94.69%)人发生删失，组织学分级为2级的患者中678 (76.27%)人发生删失，组织学分级为3级的患者中66 (45.52%)人发生删失，可以认为删失在各组的分布相似。因此，本案例数据满足条件4。

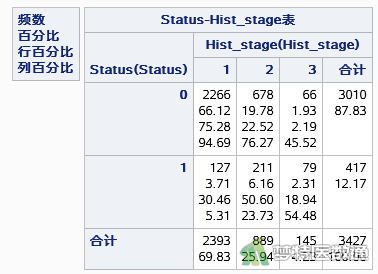
(二) 统计描述及推断

1. SAS实现

代码如下：

proc lifetest data=data1 plots=(s,ls,lls);
	time time*status(0);
	Strata Hist_stage /diff=all;
run;

其中，plots选项绘制生存曲线图，其中s绘制S图，ls绘制LS图，lls绘制LLS图；status后面括号中的数据是非结局的截尾值，在本例中也即非死亡的截尾值0；Strata后面是分组变量，在本案例中为组织学分级；diff=all表示进行两两比较。

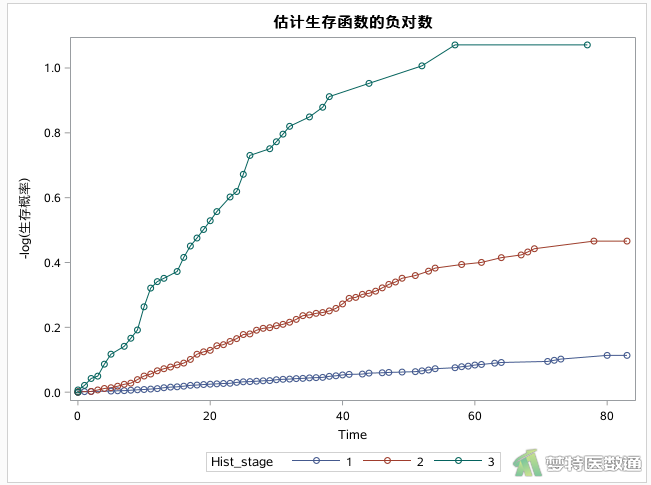
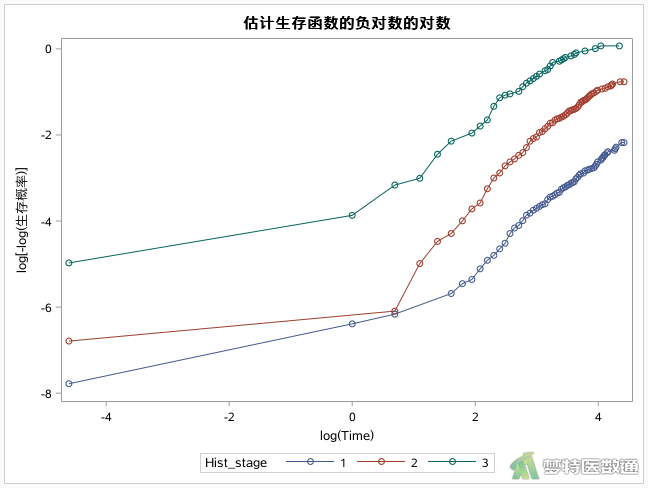
S图是生存曲线图，以生存分布函数估计值为纵坐标，时间为横坐标绘图；LS图以生存分布函数估计值的对数为纵坐标，时间为横坐标绘图；LLS图以生存分布函数估计值的对数的对数为纵坐标，时间的对数为横坐标绘图。LS和LLS图一般不作为结果展示，但可以帮助俄我们选择分析结果 。

2. 结果解读

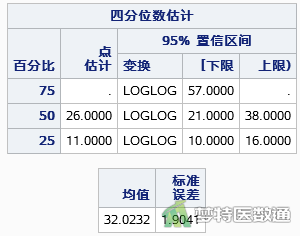
如图3—图5所示，组织学分级为1级和2级患者的中位时间缺失，表明到研究结束，未有50%的患者死亡；组织学分级为3级患者的中位生存时间为26个月，也即在第26个月的时候，50%的人死亡。

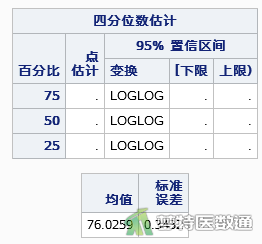
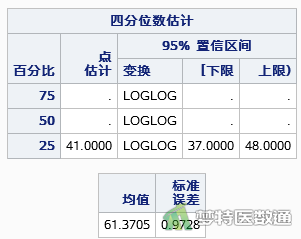
如图6所示，不同组织学分级患者的生存曲线差异有统计学意义，log-rank对数秩检验：χ²=611.9677，P<0.0001；Wilcoxon检验：χ²=627.8236，P<0.0001；-2Log(LR)似然比检验：χ²=391.1869，P<0.0001。如图7所示，多重比较结果显示，不同组织学分级患者的生存曲线两两均有差异，log-rank对数秩检验：1级VS 2级：χ²=262.7，P<0.0001；1级VS 3级：χ²=536.1，P<0.0001；2级VS 3级：χ²=17.9427，P<0.0001；Wilcoxon检验：1级VS 2级：χ²=237.6，P<0.0001；1级VS 3级：χ²=538.1，P<0.0001；2级VS 3级：χ²=5.0621，P=0.0244。

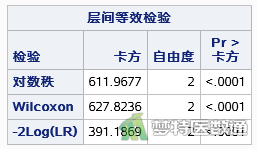
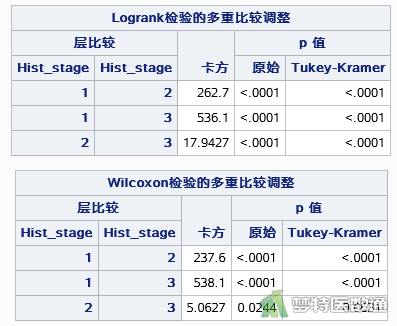
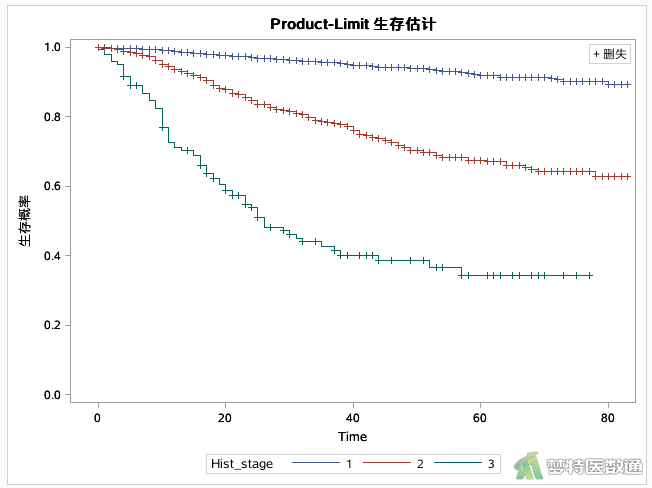
图8—图10展示了不同组织学分级患者的S图、LS图和LLS 图。如图7所示，不同组织学分级的患者之间总体生存率存在统计学差异。组织学分级为1级患者的生存率最高，组织学分级为2级患者生存率次之，组织学分级为3级患者的生存率最低。

四、结论

本研究采用Kaplan-Meier分析对不同组织学分级的宫颈癌患者的生存结果进行比较，案例数据满足条件1—4。

Kaplan-Meier分析结果表明，不同组织学分级患者的生存曲线差异有统计学意义，log-rank对数秩检验：χ²=611.9677，P<0.0001；Wilcoxon检验：χ²=627.8236，P<0.0001；-2Log(LR)似然比检验：χ²=391.1869，P<0.0001。 多重比较结果显示，不同组织学分级患者的生存曲线两两比较均有差异，log-rank对数秩检验：1级VS 2级：χ²=262.7，P<0.0001；1级VS 3级：χ²=536.1，P<0.0001；2级VS 3级：χ²=17.9427，P<0.0001；Wilcoxon检验：1级VS 2级：χ²=237.6，P<0.0001；1级VS 3级：χ²=538.1，P<0.0001；2级VS 3级：χ²=5.0621，P=0.0244。不同组织学分级的患者之间总体生存率存在统计学差异。组织学分级为1级患者的生存率最高，组织学分级为2级患者生存率次之，组织学分级为3级患者的生存率最低。

五、知识小贴士

• 删失数据：在规定的随访期内，未能观察到一些研究对象结局事件的发生，即不能得知结局事件确切的发生时间，称这类研究对象的随访时间/生存时间为删失数据，根据原因可分为三种类型：①研究结束时(已达到规定的最长观察期/随访期)，研究对象仍未出现结局事件；②由于研究对象在研究期间不再继续就诊，或拒绝访视，或失去联系等，未能观察到结局事件；③研究对象出现了竞争事件(如其他原因的死亡)，观察不到既定的结局事件而终止随访。

六、分析小技巧

• 常用的生存曲线比较的检验方法有log-rank检验、Wilcoxon检验、似然比检验。这三种方法的结果并不总是一致的，当他们的结果差别较大时，可根据S图、LS图、LLS图选择合理的结果。一般认为，当LLS图中曲线近似直线时，log-rank检验效率最高。当S图中的曲线有交叉时，log-rank检验和Wilcoxon检验的效率不如似然比检验高。只有LS图中曲线近似直线时，似然比检验效率才较高，此外似然比检验的效率都较低。
• log-rank检验对远期生存时间的权重较大，因此它主要反映了远期的生存情况；而Wilcoxon检验对早期生存时间的权重较大，因此它主要反映了近期的生存情况。如果检验结果log-rank检验有意义而Wilcoxon检验无意义，表明远期的生存差异较大，近期生存差别不大。如果检验结果log-rank检验无意义而Wilcoxon检验有意义，表明近期的生存差异较大，远期生存差别不大。如果两种检验都有意义，则表明近期和远期的差异均较大。