时间依存Cox回归模型(Time-Dependent Cox Regression Model)——SAS软件实现

关键词：SAS; Cox等比例回归; Cox回归; 生存分析; 等比例风险; 含时间依存协变量; 时依协变量

一、案例介绍

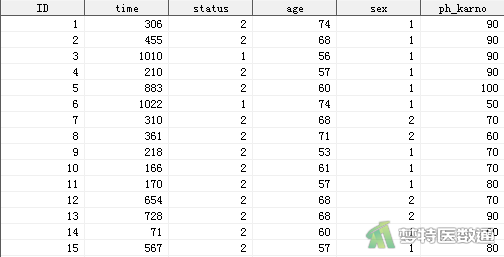
某肿瘤研究所收集了200例肺癌患者的生存数据，现欲探究患者的性别、年龄、卡氏评分与生存结局的关系，部分数据见图1。本文案例可从“附件下载”处下载。其中，ID是肺癌患者的编号，time表示患者的生存时间(天)，status表示生存状态(1=“删失”，2=“死亡”)，age表示患者年龄(岁)，sex表示患者性别(1=“男”，2=“女”)，ph_karno表示卡氏评分。

二、问题分析

本案例的目的是探究肺癌患者的性别、年龄和卡氏评分与生存结局的关系，可以采用Cox比例风险回归模型进行分析，但需要满足5个条件：

条件1：因变量是含有时间信息的二分类变量。本案例中因变量是包含生存时间的二分类资料，time是生存时间(天)；status是生存结局。本案例数据满足该条件。

条件2：各观测值之间相互独立，无互相干扰。由数据和研究设计可知，该条件满足。

条件3：一般要求结局事件的样本量为自变量个数的10~20倍(EPV原则)。该条件需要软件分析来判断。

条件4：自变量之间无严重多重共线性。该条件需要软件分析来判断。

条件5：等比例风险(Proportional hazards，PH)假设，该条件需要软件分析来判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件3判断

(1) SAS实现

首先导入数据，代码如下：

proc import datafile="G:\test\ Cox比例风险模型.csv" dbms=csv out=data1;
run;

使用如下的proc freq过程步，统计status(生存状态)的分类例数：

proc freq data=data1;
	tables status;
run;

(2) 结果解读

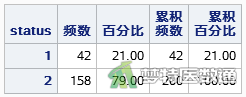
如图2所示，status(生存状态)中结局事件158例。按照EPV为10~20的原则可满足多因素模型纳入7~15个变量的需求。因此，本案例数据满足条件3。

2. 条件4判断(共线性判断)

(1) SAS实现

SAS proc reg过程步的tol和vif选项分别给出参数估计值的容忍度和方差膨胀因子，代码如下：

proc reg data=data1;	
	model status=age sex ph_karno/tol vif;
quit;

(2) 结果解读

如图3所示，容忍度的值均>0.1，方差膨胀因子的值均<5，提示自变量之间不存在严重共线性问题，因此，本案例数据满足条件4。

3. 条件5判断(等比例风险判定)

PH假定指自变量对生存率[风险比值h(t)/h0(t)]的影响不会随时间的变化而变化。若不满足PH假定，则需要改用含时间依存协变量的Cox比例模型分析数据。本案例PH假定的检验详见本章后文(多因素分析)。

 (二) 统计描述及推断

1. 统计描述

(1) SAS实现

对案例数据的性别、年龄、卡氏评分、所有研究对象的中位生存时间进行描述性统计分析，代码如下：

proc freq data=data1;
	tables sex;
run;
proc univariate data=data1;
	var age ph_karno;
run;
proc lifetest data=data1;
	time time*status(1);
run;

其中，proc lifetest语句中status后面跟的是非结局的截尾值，在本例中也即非死亡的截尾值1。

(2) 结果解读

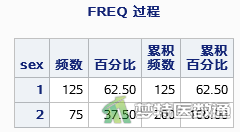
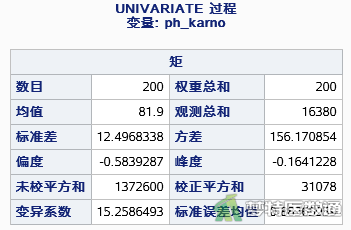
如图4—图8 所示，本研究共纳入200例肺癌患者，其中男性125例(62.50%)，女性75例(37.50%)；所有研究对象的年龄为(62.34±9.00)岁；卡氏评分为(81.90±12.50)分；所有研究对象的中位生存时间为310天，随访过程中158例(79.00%)死亡。

2. 单因素分析

(1) SAS实现

对年龄、性别、卡氏评分进行单因素分析，代码如下：

proc phreg data=data1;
	model time*status(1)=age/risklimits;
run;
proc phreg data=data1;
	model time*status(1)=sex/risklimits;
run;
proc phreg data=data1;
	model time*status(1)=ph_karno/risklimits;
run;

(2) 结果解读

单因素Cox比例风险模型分析显示(图9—图11)，年龄、性别和卡氏评分与生存结局之间均存在统计学关联(P<0.1)，年龄每增加一岁肺癌患者的死亡风险增加1.7% (HR=1.017，95%CI：0.999~1.036；P=0.0694)；女性死亡风险比男性低38.7% (HR=0.613，95%CI：0.439~0.857；P=0.0041)；卡氏评分每上升一个单位肺癌患者死亡的风险下降1.5% (HR=0.985，95%CI：0.974~0.997；P=0.0129)。

3. 多因素分析

将单因素Cox比例风险模型分析中有统计学关联的变量(年龄、性别、卡氏评分)纳入到多因素Cox比例风险模型，并对变量进行等比例风险判定。

(1) SAS实现

proc phreg data=data1;
	model time*status(1)=age sex ph_karno/risklimits;
	assess var=(age) ph/resample;
	assess var=(sex) ph/resample;
	assess var=(ph_karno) ph/resample;
run;

其中，assess语句对变量进行等比例风险判定，resample选项表示用1000次模拟的kolmogorov_type supremurn检验来验证该假定。

(2) 结果解读

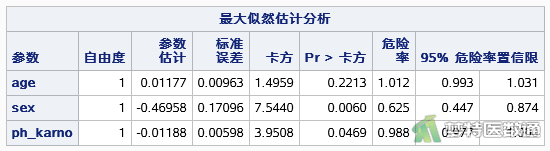
如图12所示，性别和卡氏评分与生存结局之间存在统计学关联(P<0.05)，女性的死亡风险比男性低37.5% (HR=0.625,95%CI：0.447~0.874；P=0.0060)；卡氏评分每增加一个单位，肺癌患者死亡风险下降1.2%(HR=0.988；95%CI：0.977~1.000；P=0.0469)。年龄每增加一岁肺癌患者的死亡风险增加1.2% (HR=1.012，95%CI：0.993~1.031；P=0.2213)，但关联无统计学意义。

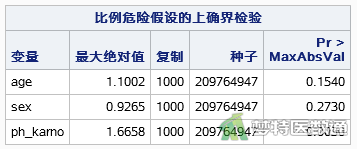
对多因素Cox比例风险模型中的自变量进行PH假定检验，如图13所示，结果显示年龄和性别的P值均>0.1，而卡氏评分(phkarno)的P值<0.05，提示年龄和性别满足PH假定，卡氏评分不满足PH假定；提示不满足条件5。

4. 含时间依存协变量的Cox比例风险模型

由于卡氏评分不满足PH假定，因此需要设立卡氏评分与时间的交互项，与年龄、性别、卡氏评分一起建立含时间依存协变量的Cox比例风险模型。

(1) SAS实现

proc phreg data=data1;
	model time*status(1)=age sex ph_karno phkarno_time/risklimits;
	phkarno_time=ph_karno*time;
run;

其中，phkarno_time表示卡氏评分与时间的交互项。

(2) 结果解读

如图14所示，卡氏评分与时间的交互项(phkarno_time)有统计学意义(P=0.0116)，提示卡氏评分具有时间依存性，进一步证实了其不满足风险比例Cox回归模型的PH假定要求，故此处应采用时间依存协变量Cox回归模型。

分析结果显示，性别的效应值HR为0.615，表示女性死亡的风险比男性低38.5% (HR=0.615，95%CI：0.440~0.860；P=0.0045)；年龄与生存结局的关联无统计学意义 (HR=1.013，95%CI：0.994~1.032；P=0.1868)；卡氏评分的时依系数β(t)=-0.03425+0.0000704×time，效应值HR=exp(-0.03425+0.0000704×time)。例如，当时间为200天时，卡氏评分对应的HR=exp(-0.03425+0.0000704×200)= 0.980。

四、结论

本研究采用Cox比例风险模型探究年龄、性别、卡氏评分与肺癌患者生存结局的关系，数据样本量满足要求，自变量之间无严重多重共线性；PH假定检验发现卡氏评分不满足PH假定(P=0.003)，需要建立含时间依存协变量的Cox比例风险模型。

含时间依存协变量的Cox比例风险模型分析结果表明，性别和卡氏评分均是肺癌患者生存结局的影响因素，其中女性死亡的风险比男性低38.5% (HR=0.615，95%CI：0.440~0.860；P=0.005)；年龄与生存结局的关联无统计学意义 (HR=1.013，95%CI：0.994~1.032；P=0.187)；卡氏评分的时依系数β(t)=-0.03425+0.0000704×time，效应值HR=exp(-0.03425+0.0000704×time)。

五、分析小技巧

• 对于生存数据，如果自变量是分类变量，可以使用Kaplan-Meier生存曲线和log-rank检验进行单因素分析，也可以使用单因素Cox比例风险模型；如果自变量是定量变量，一般单因素分析采用Cox比例风险模型。