Kruskal-Wallis H检验(Kruskal-Wallis H Test)用于推断计量资料或等级资料的多个独立样本所来自的多个总体分布是否有差别。在理论上检验假设H0应为多个总体分布相同,即多个样本来自同一总体。由于H检验对多个总体分布的形状差别不敏感,故在实际应用中检验假设H0可写作多个总体分布位置相同。对立的备择假设H1为多个总体分布位置不全相同。
关键词:非参数检验; 秩和检验; 多样本Kruskal-Wallis H检验; Kruskal-Wallis H检验; 多样本秩和检验; 事后检验
一、适用条件
条件1:有一个观察变量和一个分组变量。
条件2:观察变量为非正态分布或方差不齐的连续变量或有序分类变量。
条件3:存在多个分组(k≥2)。
条件4:观察变量是相互独立的观测值。
二、统计量计算
(一) 多个独立样本比较的Kruskal-Wallis H检验
1. 多个独立样本计量资料比较的Kruskal-Wallis H检验
当数据为不服从正态分布的计量资料时,如一些百分率、时间资料,其多组间的比较使用Kruskal-Wallis H检验。
其检验统计量H值的计算过程为:①把各组数据混合从小到大编秩,遇数据相等者取平均秩;②设各组例数为 \( n_{i}\left(\sum n_{i}=N\right) \) ,秩和为Ri,按下式求H值。
\( H=\frac{12}{N(N+1)}\left(\sum \frac{R_{i}^{2}}{n_{i}}\right)-3(N+1) \)当各数据存在相同秩较多时,按上述公式计算所得的H值偏小,可按下式求校正Hc值。
\( H_{c}=H / C, \quad C=1-\sum\left(t_{j}^{3}-t_{j}\right) /\left(N^{3}-N\right) \)式中tj为第j个相同秩次的个数。
当组数g=3和每个组例数ni≤5时,查(H界值表),确定P值,作出推断结论。
当组数g=3且最小例数大于5或g>3时,H或Hc近似服从自由度为v=g-1的χ2分布,可查(χ2界值表),确定P值,作出推断结论。
2. 多个独立样本频数表资料和等级资料比较的Kruskal-Wallis H检验
当数据为频数表资料时,是按数量区间分组;等级资料是按等级分组,其多组间的比较使用Kruskal-Wallis H检验。其检验统计量Hc值的计算过程为:① 先确定各数量区间或等级的合计人数、秩次范围和平均秩次;②分组求秩和,Ri是用各区间或等级的频数与相应平均秩次相乘再求和所得;③按上述两个公式求检验统计量Hc。
按自由度v=g-1查(χ2界值表)确定p值,作出推断结论。
计量资料(非正态或方差不齐)或等级资料的两独立样本比较,即可用两个独立样本比较的Wilcoxon秩和检验公式,也可用本节介绍的Kruskal-Wallis H检验公式,两者的关系是:H(或Hc)=u2。
3. Kruskal-Wallis H检验的原理
(1) H界值表制作原理
为简单起见,假定3个组例数n1=3,n2=3,n3=2。则N=n1+n2+n3=7,总体秩为1,2,3,4,5,6,7。第一个组从总体7个秩中取3个秩,第二个组从总体余下的4个秩中取2个秩,第三个组取总体最后余下的2个秩,3个组取秩的可能组合情况有210种\( \left[\left(\begin{array}{l}7\\3\end{array}\right)\left(\begin{array}{l}4\\2\end{array}\right)\left(\begin{array}{l}2\\2\end{array}\right)=210\right] \)。对3个组取秩的每种组合情况,先求3个组的秩和R1、R2和R3,再用上述求H值的公式求H值,就有210个H值,最后归纳整理即得N=7和n1=3,n2=3,n3=2时H的概率分布。
H的概率分布是偏态的非连续分布。3个组的平均秩 \( \bar{R}_{1} \) 、 \( \bar{R}_{2} \) 和 \( \bar{R}_{3} \) 相等时,H=0; \( \bar{R}_{1} \) 、 \( \bar{R}_{2} \) 和 \( \bar{R}_{3} \) 的差别越小,H值越小(越接近0); \( \bar{R}_{1} \) 、 \( \bar{R}_{2} \) 和 \( \bar{R}_{3} \) 的差别越大,H值越大。根据H的概率分布,可确定不同概率水平(如0.05、0.01)下H的上侧界值。如果H0成立,H值越小,P值越大。
(2) H的χ2近似法原理
设有g个组,每个组的例数用ni表示,n1+n2+…+ ng=N。总体秩为1,2,…,N。每个组从总体中取ni个秩,其秩和用Ri表示,则有 \( \mu_{R_{i}}=n_{i}(N+1) / 2 \) , \( \sigma_{R_{i}}^{2}=n_{i} N(N+1) / 12 \) 。而 H=χ2= \( \sum\left(R_{i}-\mu_{R_{i}}\right)^{2} /\sigma_{R_{i}}^{2}\) ,故得上述第一个公式;若N个秩中有相同秩, \( \mu_{R_{i}} \) 不变,可证明 \( \sigma_{R_{i}}^{2}=\left[n_{i} N(N+1) / 12\right]\left[1-\sum\left(t_{j}^{3}-t_{j}\right) /\left(N^{3}-N\right)\right] \) ,故得上述第二个公式。H或Hc近似服从自由度为v=g-1的χ2分布。
(二) 多个独立样本两两比较的Nemenyi法检验
当经过多个独立样本比较的Kruskal-Wallis H检验拒绝H0,接受H1,认为多个总体分布位置不全相同时,若要进一步推断是哪两个总体分布位置不同,可用Nemenyi检验(Nemenyi test)或扩展的t检验法
1. Nemenyi检验
设有g个组,当各组例数较大时,按下式求第i个组和第j个组比较的χ2值:
χ2= \( \frac{\left(\bar{R}_{i}-\bar{R}_{j}\right)^{2}}{\frac{N(N+1)}{12}\left(\frac{1}{n_{i}}+\frac{1}{n_{j}}\right)C} \) , \( v=g-1 \)
C为校正系数,计算公式如下:
\( C=1-\sum\left(t_{j}^{3}-t_{j}\right) /\left(N^{3}-N\right) \)按v=g-1查(χ2界值表)确定p值,作出推断结论。
2. 扩展的t检验法
各组例数相等或不等时均可适用,统计量t值的计算公式如下:
\( t=\frac{\left|\bar{R}_i-\bar{R}_j\right|}{\frac{N(N+1)(N-1-H)}{12(N-g)}\left(\frac{1}{n_{i}}+\frac{1}{n_{j}}\right)}{} \) , \( v=N-g \)
式中 \( \bar{R}_{i}及\bar{R}_{j} \) 为A组与B组的平均秩次,ni与nj为样本含量;g为处理组数;N为总例数;H为Kruskal-Wallis的H检验中算得的统计量H或Hc值。上式中分母为 \( (\left(\bar{R}_{i}-\bar{R}_{j}\right) \) 的标准误。
三、案例数据
某医师对30名胆管癌患者的肿瘤直径进行了测定,其中9名患者肿瘤直径<2cm (A组),11名患者肿瘤直径为2~3cm (B组),10名患者肿瘤直径>3cm (C组)。同时该医生对所有患者血清中癌抗原19-9 (cancer antigens 19-9, CA19-9)水平(μg/L)进行了测定,问不同肿瘤直径的胆管癌患者CA19-9水平是否不同?数据见图1。
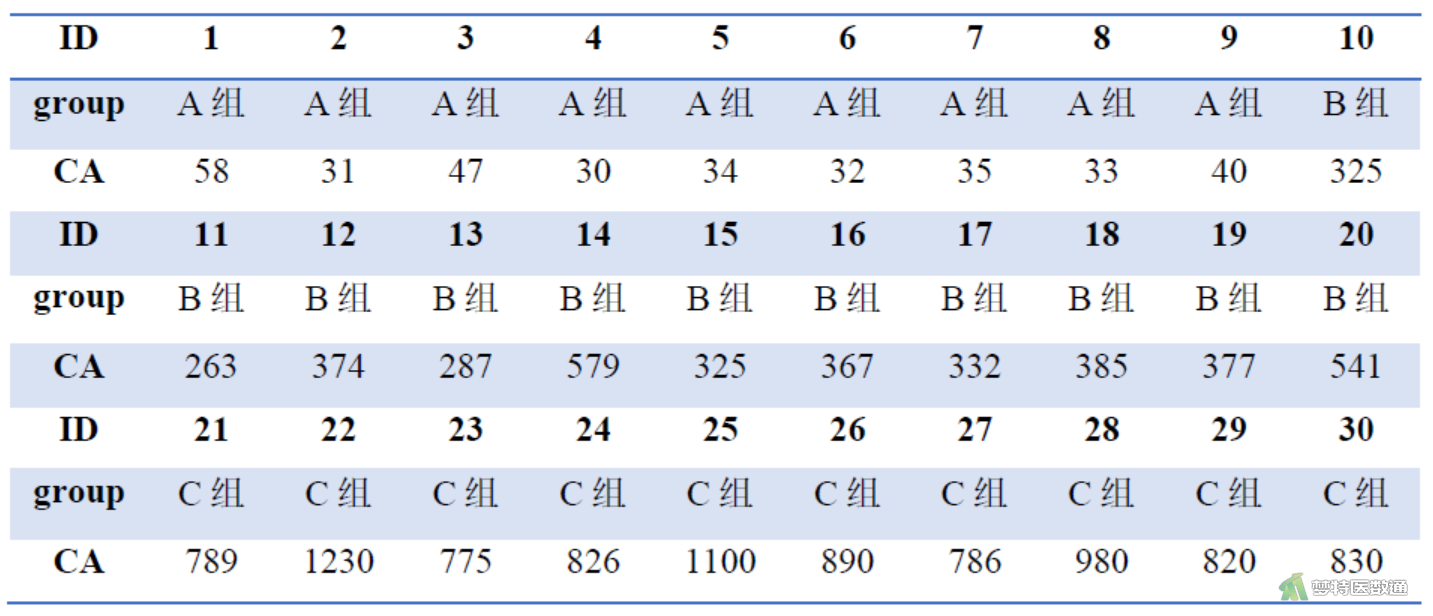
四、假设检验
本例资料经 “Normality Test (Shapiro-Wilk) (夏皮罗-威尔克正态性)”正态性检验结果显示A、B、C三组的P值分别为0.023、0.035和0.016,均<0.1,提示三组数据不服从正态分布。Levene’s方差齐性检验结果显示,F=7.192,P=0.003<0.1,提示三组数据方差不齐。本案例中三组连续变量数据既不服从正态分布,也不满足方差齐性,可以考虑使用Kruskal-Wallis H检验。
(一) 建立检验假设,确定检验水准
H0:不同肿瘤直径的胆管癌患者CA19-9水平总体分布位置相同
H1:不同肿瘤直径的胆管癌患者CA19-9水平总体分布位置不同
α=0.05 。
(二) 计算检验统计量
1. 编秩
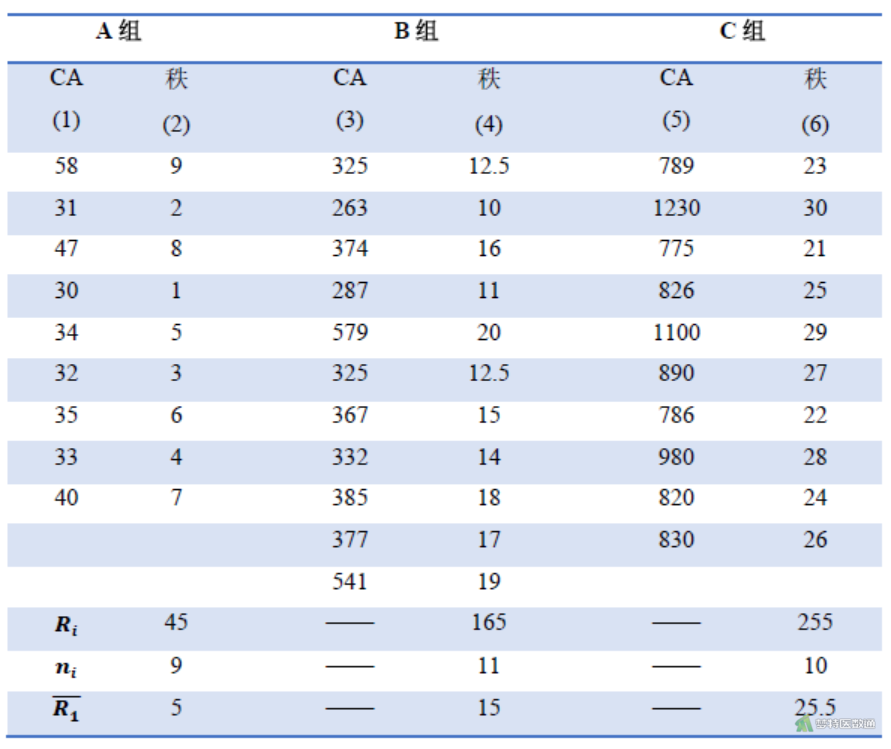
把三组数据混合从小到大编秩,遇数据相同者取平均秩,编秩结果即图2中(2)、(4)、(6)列。
2. 求例数、秩和
分别求出三组数据例数ni、秩和Ri及平均秩 \( \bar{R}_{1} \) ,结果即图2中ni、Ri和 \( \bar{R}_{i} \) 行。
3. 计算统计量H值
由于本数据相同秩的个数较少,可直接求H值统计量。
据N=∑ni本例N=9+11+10=30。按上述公式可计算
\( H=\frac{12}{30(30+1)}\left(\frac{45^{2}}{9}+\frac{165^{2}}{11}+\frac{255^{2}}{10}\right)-3(30+1)=25.742 \)如果要求校正Hc值统计量,则计算过程如下:
\( c=1-\frac{\left(2^{3}-2\right)}{30^{3}-30}=0.9997775 \)Hc=25.742/0.9997775=25.74773
可见H和Hc统计量相差不大。
(三) 确定P值,作出推断结论
自由度v=3-1=2。因g=3,本例各组最小例数大于5,故查(χ2界值表)得P<0.005,按α=0.05水准,拒绝H0,接受H1,可认为不同肿瘤直径的胆管癌患者CA19-9水平不全相同。
(四) 事后检验
虽然得到了“三种不同肿瘤直径的胆管癌患者的CA19-9水平不全相同”的结论,但我们仍然不清楚到底是哪两组之间不同,因此需要使用进一步两两比较,两两比较的方法较多,此处介绍Nemenyi检验与扩展的t检验法。
1. Nemenyi检验
(1) 建立检验假设,确定检验水准
H0:任意两种肿瘤直径的胆管癌患者CA19-9水平相同
H1:任意两种肿瘤直径的胆管癌患者CA19-9水平不同
α=0.05 。
(2) 计算检验统计量
本例已算得C=0.9997775。根据图2下部ni行和 \(\bar{R}_{i}\) 行数据,按上述公式可计算A组和B组相比:
\( \chi_{A, B}^{2}==\frac{(5-15)^{2}}{\frac{30(30+1)}{12}\left(\frac{1}{9}+\frac{1}{11}\right) \times 0.9997775}=6.388518 \)(3) 确定P值,作出推断结论
自由度v=3-1=2。据 \( \chi_{A, B}^{2}=6.388518 \) 查(χ2界值表)得0.025<P<0.05,可认为肿瘤直径<2cm的患者和2~3cm的患者CA19-9水平差异有统计学意义。
同样可算得: \( \chi_{A, C}^{2}=25.69162, [latex] \chi_{B, C}^{2}=7.453271 \) 据 \( \chi_{A, C}^{2}=25.69162 \) 查(χ2界值表)得P<0.005,可认为肿瘤直径2~3cm的患者和>3cm的患者CA19-9水平差异有统计学意义;据 \( \chi_{B, C}^{2}=7.453271 \) 查(χ2界值表)得0.01<P<0.025,可认为肿瘤直径<2cm的患者和>3cm的患者CA19-9水平差异有统计学意义。
2. 扩展的t检验法
(1) 建立检验假设,确定检验水准
H0:所比较的两个不同组别的肿瘤直径的胆管癌患者CA19-9水平总体分布位置相同
H1:所比较的两个不同组别的肿瘤直径的胆管癌患者CA19-9水平总体分布位置不同
α=0.05 。
(2) 计算检验统计量
列出两两比较计算表,求得t值。见图3。

图3中第(5)栏为按上述求统计量t值公式计算得的t值。本例N=30,g=3,Hc=25.74773,则(A)与(B)比较的t值为:
\( t=\frac{|5-15|}{\frac{30(30+1)(30-1-25.74773)}{12(30-3)}\left(\frac{1}{9}+\frac{1}{11}\right)}=5.3025 \)仿此得图3第(5)栏。
(3) 确定P值,作出推断性结论
根据图3中第(5)栏中的t值,按自由度v=30-3=27查(t界值表),界定P值,见图3第(6)栏。
据上可知肿瘤直径<2cm的患者和2~3cm的患者CA19-9水平差异有统计学意义,2~3cm的患者和>3cm的患者CA19-9水平差异有统计学意义,<2cm的患者和>3cm的患者CA19-9水平差异有统计学意义。