单因素协方差分析(One-Way ANCOVA)——SAS软件实现

关键词：SAS; 协方差分析; 单因素协方差分析; 平行性检验; 平行线检验

一、案例介绍

为研究A、B、C三种饲料对增加小鼠体重的影响，将初始体重相近的45只小鼠随机分成三组，分别喂养A、B、C三种饲料，但在实验设计时未对小鼠的进食量加以限制，现测得三组小鼠的进食量(Food)和所增体重(Weight)，请推断A、B、C三种饲料对小鼠的增重效果是否有差别？部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较A、B、C三种饲料对增加小鼠体重的影响，即A、B、C三组小鼠体重增量是否存在差异。但显然，每只小鼠的进食量会对体重增量产生影响，因此针对这种情况可将进食量作为体重增量的影响因素进行单因素协方差分析。但需要满足9个条件：

条件1：观察变量为连续变量。本研究中观察变量为体重增量，为连续变量，该条件满足。

条件2：自变量为二分类或多分类变量。本研究中自变量为A、B、C三组，该条件满足。

条件3：协变量是连续变量。本研究中协变量为进食量，为连续变量，该条件满足。

条件4：各研究对象之间具有独立的观测值。本研究中各个研究对象均为独立样本，不存在互相干扰的情况，该条件满足。

条件5：观察变量不存在显著异常值，该条件需要通过软件分析后判断。

条件6：各组内因变量的残差服从正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件7：组间因变量的残差方差齐，该条件需要通过软件分析后判断。

条件8：各组内协变量和因变量之间存在线性关系，该条件需要通过软件分析后判断。

条件9：各组内协变量和因变量的回归直线平行，即通过平行性检验，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

①利用LIBNAME语句建立SAS逻辑库关联，注意逻辑库名称要求，即最大长度8字符，必须以字母或下划线“_”开始，可以是字母、数字和下划线的任意组合。具体代码如下：

libname mydata 'D:\mydata';

通过这一步骤，SAS能够识别引号中的物理位置，将逻辑库建立在该目录下，同时在以下过程中新建的SAS表格便可以永久储存在该位置，便于反复读取和使用。先运行该代码使其生效。

②利用PROC IMPORT语句导入文件，代码如下：

proc import out= mydata.example
datafile=" D:\mydata\单因素协方差分析.csv "
dbms=csv replace;
getnames=yes;
run;

该过程在mydata逻辑库中生成example数据集，数据文件由DATAFILE=选项指定，DBMS=选项指定其数据库类型。该案例中初始数据集为csv文件，故而使用“dbms=csv”指定。如果已经存在相同名称的SAS数据集，即可使用REPLACE选项进行覆盖。GERNAMES=YES选项指定从第2行开始读取数据，将数据集的首行变量名作为SAS数据集的变量名。

(二) 适用条件判断

条件6和条件7需要使用残差进行判断，先使用单因素协方差分析生成因变量残差。

1. 生成因变量残差

(1) 软件操作

运用REG过程计算残差，具体代码如下所示：

Proc reg data=mydata.example;
by group;
model weight=food/r;
output out=mydata.example2 r=residual; 
run; 
quit;

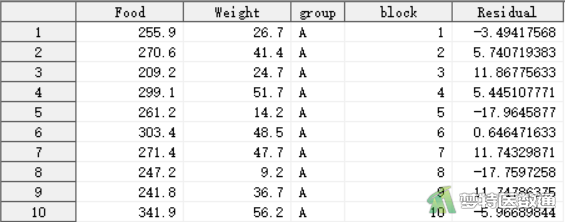
BY语句以“group”变量分组计算残差，MODEL语句以“weight”为因变量，“food”作为协变量计算残差的值。OUTPUT语句将残差输入新建的表“mydata.example2”，新建变量命名为“residual”。“r=residual”将该步骤中计算的残差输入至新表。

(2) 结果解读

以上步骤生成了一列新的变量“Residual (残差)”(图2)。

2. 条件5判断(异常值判断)

(1) 软件操作

运用UNIVARIATE语句进行检验，具体代码如下所示：

proc univariate data=mydata.example2 normal plot;
class group;
var residual;
run;

此处对新建的表“mydata.example2”进行分析。PLOT选项作平行条状图，箱线图和正态概率图。CLASS语句以“group”分组分别分析A、B、C三种饲料的残差是否存在异常值。

(2) 结果解读

图3—图5分别为A、B、C三种饲料的残差的平行条状图、箱线图和正态概率图，未提示任何异常值和极端值，满足条件5。

3. 条件6判断(正态性检验)

(1) 软件操作

运用前一步骤中UNIVARIATE语句中NORMAL选项进行检验。

(2) 结果解读

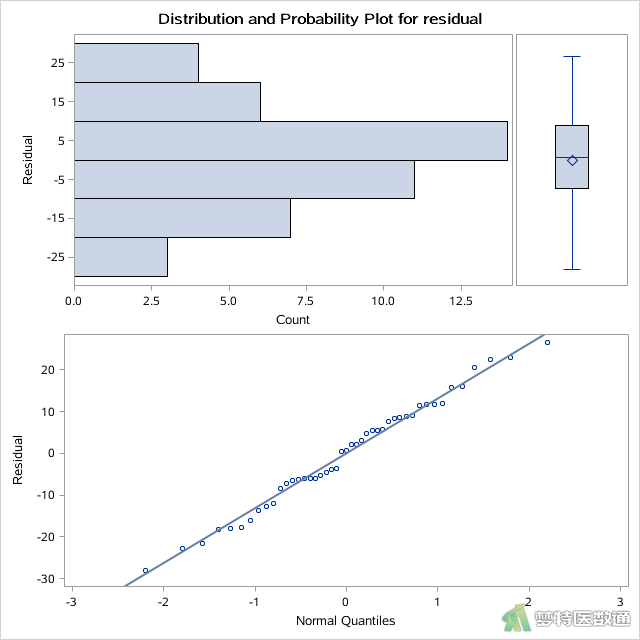
图6显示了残差的“Tests for Normality (正态性检验)”结果，“Shapiro-Wilk (夏皮罗-威尔克正态性)”检验的结果显示整体残差正态性检验的P值为0.8064，>0.1。可认为整体残差服从正态分布。此外，本案例也可以绘制残差的Q-Q图，如7中所示，结果也提示残差满足正态性要求。综上，本案例满足条件6。

4. 条件7判断(方差齐性检验)

(1) 软件操作

运用ANOVA过程进行检验，具体代码如下所示：

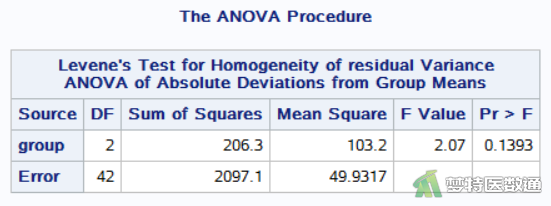
proc anova data=mydata.example2;
class group;
model residual=group;
means group / hovtest=levene(type=abs);
run;

此处对新建的表“mydata.example2”进行分析。该步骤中，CLASS语句指定分类变量“group”。MODEL语句指定分析因素“residual (残差)”与响应变量“group”。 MEANS语句计算均数和方差，其常见选项HOVTEST可指定分析方法，此处我们使用LEVENE检验，“(type=abs)”指定该过程计算绝对值(absolute value)进行分析。

(2) 结果解读

图9 “Levene's Test for Homogeneity (Levene’s方差齐性检验)”的结果显示，统计量F=2.07、P=0.1393；提示数据总体方差相等，满足条件8。

5. 条件8判断(线性关系检验)

(1) 软件操作

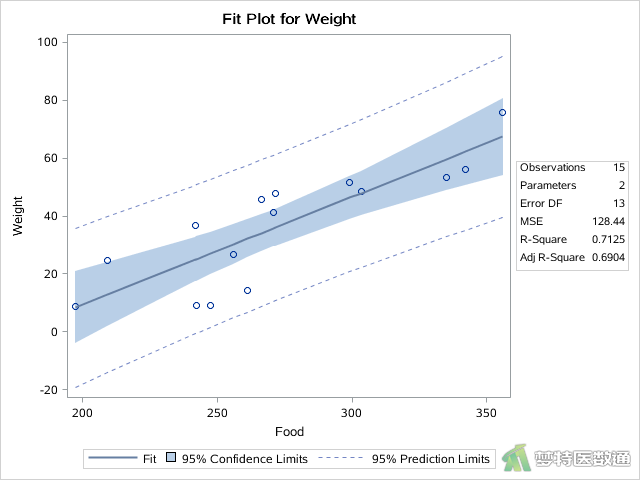
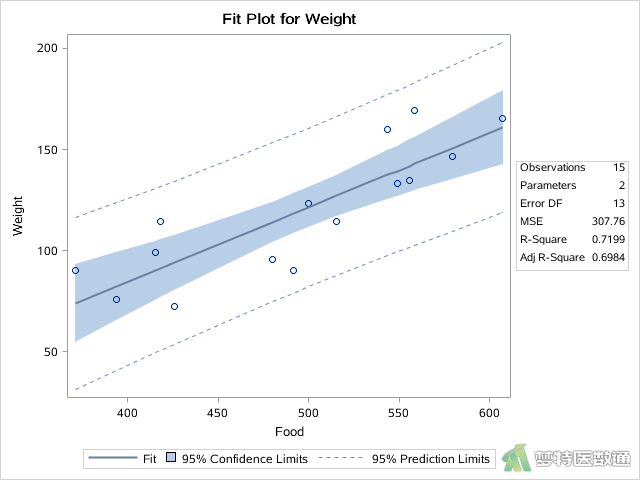
①前一步骤的REG过程给出了“Food”与“Weight”的“Fit Plot (拟合线图)”，A、B、C三组分别如图9—图11所示。

② 运用CORR步骤计算“Pearson Correlation Coefficients (皮尔森相关系数)”，具体代码如下所示：

proc corr data=mydata.example2 ;
var weight;
with food;
by group;
run;

此处对新建的表“mydata.example2”进行分析。其中VAR语句和WITH 语句指定分析“weight”和“food”两变量间的线性关系，BY语句指定以“group”变量分组，该步骤结果如图12—图14所示。

(2) 结果解读

由图9—图11可知，A、B、C三组内“Food”与“Weight”均呈现线性关系；图12—图14列出了三组的“Pearson Correlation Coefficients (皮尔森相关系数)”，可见相关系数均较高(>0.8)，P值均<0.0001。综上，本案例各组内协变量和因变量之间均存在线性关系，满足条件8。

5. 条件9判断(平行性检验)

平行性检验通过判断group与Food的交互项是否有统计学意义决定。

(1) 软件操作

运用GLM步骤进行检验，具体代码如下所示：

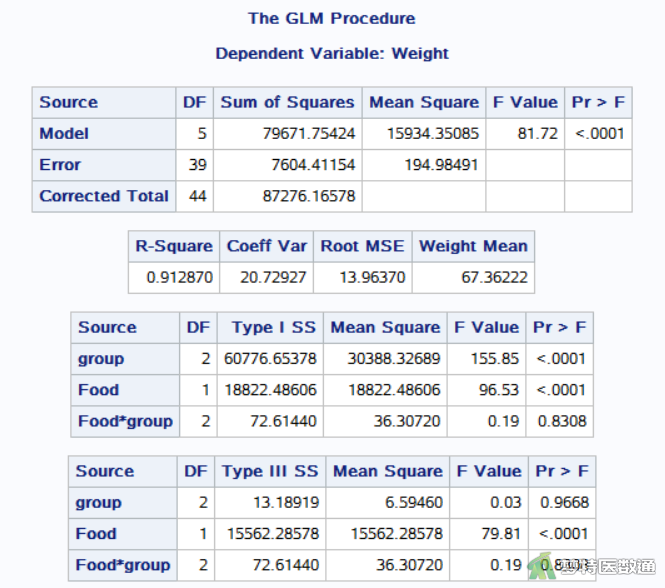
proc glm data=mydata.example2 ;
class group;
model weight=group food group*food;
run;
quit;

此处对新建的表“mydata.example2”进行分析。MODEL步骤中“group*food”项即对group与Food的交互项是否有统计学意义进行检验。

(2) 结果解读

在图15 GLM步骤所得表格中，第一张表为整体模型检验结果，其中“Model (模型)”行的F =81.72，P<0.001，表示整体模型检验具有统计学意义。后两张表中均可得到“group*food”的交互项检验结果，由于“group*food”交互项放于模型最后一项，属于调整了“group”和“food”之后的交互作用，故而其“Type I SS (I类平方和)”和“Type III SS (III类平方和)”结果相等。检验结果为F_group*Food =0.19，P_group*Food=0.8308，表示交互项无统计学意义，即满足平行性检验。因此，本案例满足条件9。

(三) 统计描述

1. 软件操作

运用UNIVARIATE语句可得各组数据的统计描述结果。与前一步骤中相似，但分析变量为“weight”和“food”，具体代码如下所示：

proc univariate data=mydata.example2;
class group;
var residual;
run;

2. 结果解读

图16-图18中列出了A、B、C三组“weight”的统计描述结果。体重增量分别为36.633±20.369、46.427±21.389、119.027±31.944 g。

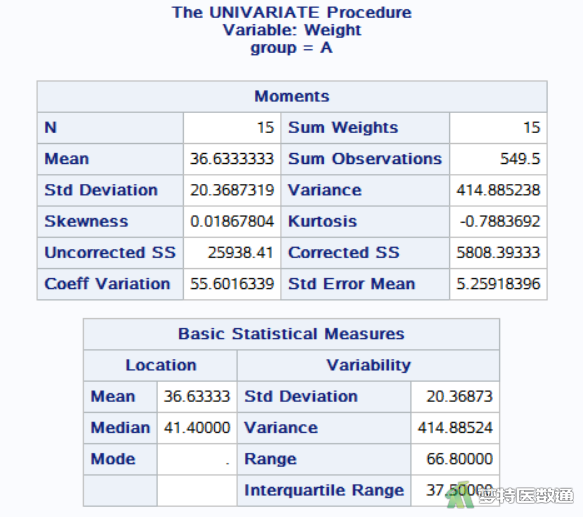
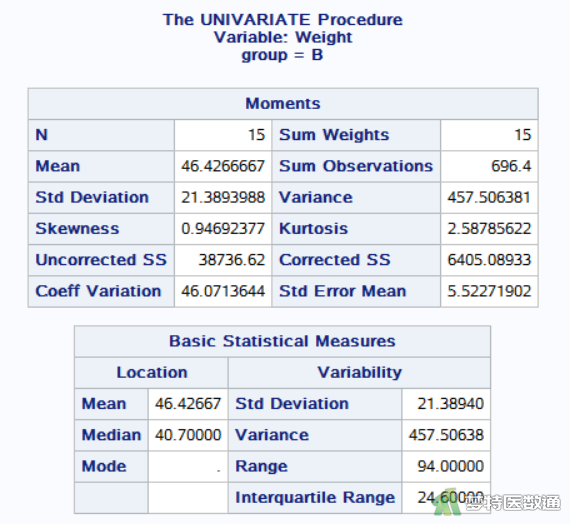
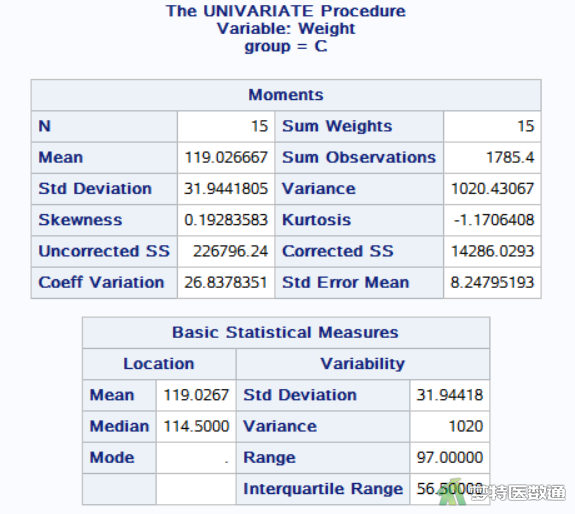
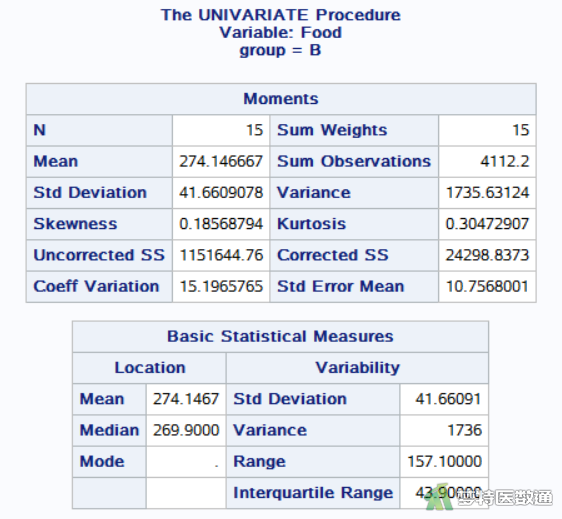
图19-图21为三组“food”的统计描述结果。三组的进食量分别为273.220±46.247、274.147±41.661、493.587±73.797 g。

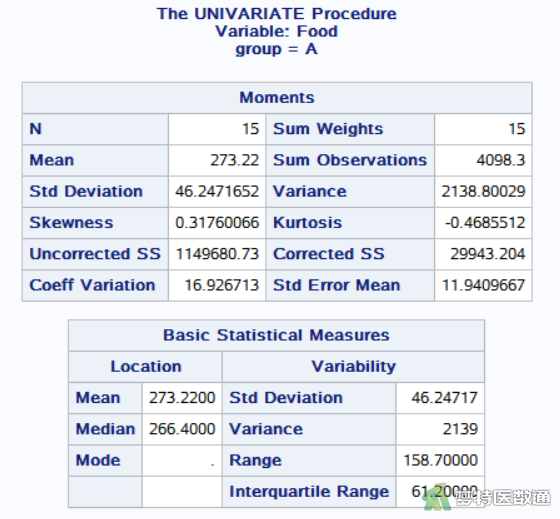
(四) 单因素协方差分析

1. 统计学描述

(1) 软件操作

运用GLM步骤进行检验，具体过程如下所示：

proc glm data=mydata.example2 plot=meanplot(cl);
class group;
model weight=group food/solution;
lsmeans group/stderr pdiff cl;
run;
quit;

PLOT选项生成估算边际均值图。MODEL步骤中，由于交互作用group*food无统计学意义，故而用“weight=group food”模型。SOLUTION选项输出回归系数的估计值标准误差和假设检验等。LSMEANS步骤输出最小二乘均值的结果，包括STDERR (标准误)、PDIFF (P值)和CL (置信区间)等。

(2) 结果解读

图22 “Least Squares Means (最小二乘均值)”表格中提供了“weight”三组的“LSMean (最小二乘均值)”、“Standard Error (标准误)”及P值，A、B、C三组体重增量的估算边际均值分别为64.649 (95%CI: 55.552~73.746)、74.091 (95%CI: 65.037~83.144)、63.347 (95%CI: 50.054~76.640) g，P值均<0.0001。可见三组体重增量的估算边际均值与三组体重增量的均值(图16-图18)存在较大差异。图22的估算边际均值图也绘制了三组体重增量的情况，可见B组最高、A组其次、C组最低。但这种差异是否具有统计学意义，还需要依据统计学推断结果做出判断。

2. 统计学推断

(1) 软件操作

通过前一步骤GLM过程得到检验结果。

(2) 结果解读

图24中“Type III SS (III类平方和)”为校正后结果，显示Food这一行的F_Food=100.52，P_Food<0.001，提示Food的确对Weight具有影响，因此需要将其列为协变量进行控制。Group这一列的F_group=2.00，P_group=0.1485，提示三组小鼠体重的增重效果差异无统计学意义。

(五) 事后检验(两两比较)

本案例中由于三组间整体比较差异无统计学意义，因此无须再进行事后两两比较。假设本案例三组间整体比较差异有统计学意义，其分析步骤如下。

1. 软件操作

运用前一步骤中GLM过程可得未校正的P值，添加“adjust=bon”选项可得“Bonferroni (邦弗罗尼)”校正法的P值。具体代码如下：

proc glm data=mydata.example2 plot=meanplot(cl);
class group;
model weight=group food/solution;
lsmeans group/ stderr pdiff cl adjust=bon;
run;
quit;

2. 结果解读

图25 “Least Squares Means (最小二乘平均)”表格中提供了各组两两比较的 “P_bonferroni (校正P值)”。可知，三组中任意两组比较差异均无统计学意义(P>0.05)。

四、结论

本研究采用单因素协方差分析，判断在调整进食量后A、B、C三种饲料对小鼠的增重效果是否有差别。通过对模型残差绘制箱线图提示，数据不存在异常值；通过Shapiro-Wilk检验，提示因变量残差满足正态性要求；通过Levene’s检验，提示各组因变量残差满足方差齐性要求；通过绘制散点图和相关性分析，提示各组内协变量和因变量之间存在线性关系；通过平行性检验，发现“group*Food”的交互项无统计学意义(F_group*Food =0.19，P_group*Food=0.8308)，提示满足平行性检验要求。

A、B、C三组小白鼠体重增量分别为36.633±20.369、46.427±21.389、119.027±31.944 g。单因素协方差分析显示，在调整进食量后A、B、C三组体重增量的估算边际均值分别为64.649 (95%CI: 55.552~73.746)、74.091 (95%CI: 65.037~83.144)、63.347 (95%CI: 50.054~76.640) g，差异无统计学意义(F_group=2.00，P_group=0.1485)。本研究结果提示A、B、C三种饲料对小白鼠体重的增重效果无差异。

五、知识小贴士

• 协方差分析是针对在实验设计阶段难以控制其取值水平，或者无法严格控制的因素，在统计分析阶段对其进行统计控制的一种分析方法，实质为线性回归分析和方差分析的结合。适用于完全随机设计、随机区组(配伍)设计、拉丁方设计、析因设计等类型的方差分析。
• 协方差分析一般要求协变量在组间的观察范围相差不宜太大(分析前最好先对协变量均数间的差别作假设检验)，否则修正后的边际均值的差值可能会落在回归线的延长线上，回归线外推后，是否仍然满足平行线和线性关系尚不可知，其协方差分析的结论可能不一定准确。

六、分析小技巧

• 正态性检验：对协方差分析的正态性条件考察应检验因变量残差的正态性，此时检验多组整体残差的正态性即可，无须检验每组残差的正态性。在SAS中采用UNIVARIATE 过程得到“Shapiro-Wilk (夏皮罗-威尔克正态性)”检验的结果。关于正态性检验的注意事项详见文章医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现。
• 方差齐性检验：对协方差分析的方差齐性条件考察应检验组间因变量残差是否相等。在SAS中运用ANOVA过程进行检验。关于方差齐性检验的更多内容请阅读医学统计学核心概念及重要假设检验的软件实现(4/4)——方差齐性检验及SPSS实现。