Friedman检验 (The Friedman Non-parametric Repeated Measures ANOVA Test)——SAS软件实现

关键词：SAS; 非参数检验; 秩和检验; Friedman检验; 重复测量非参数检验

一、案例介绍

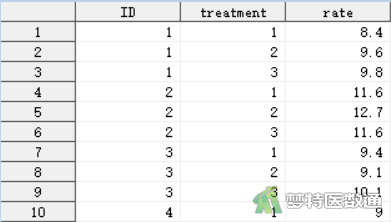
8名受试对象在相同试验条件下分别接受A、B、C 3种不同频率振动的刺激，测量其反应率(%)，问3种频率振动刺激的反应率是否有差别？部分数据见图1。本文案例可从“附件下载”处下载。

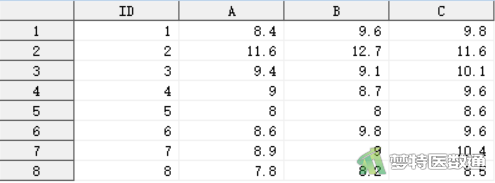
二、问题分析

本案例的分析目的是判断多组相关数据的差异，首先对三组数据进行正态性检验，若发现不服从正态分布，可以使用Friedman检验(此处的“反应率”是针对个体观察对象所测得的一个反应程度的指标，可以理解为“反应指数”，因此属于连续变量)。Friedman检验可应用于多组配对或相关数据的秩转换非参数检验，但需要满足2个条件：

条件1：观察变量为连续变量或有序分类变量。本研究中反应率为连续变量，该条件满足。

条件2：观察变量具有3个及以上的分组，为配对设计，或各组之间存在相关性。本研究中3组数据均是对同一批研究对象所测量，该条件满足。

三、软件操作及结果解读

(一) 导入数据

①利用LIBNAME语句建立SAS逻辑库关联，注意逻辑库名称要求，即最大长度8字符，必须以字母或下划线“_”开始，可以是字母、数字和下划线的任意组合。具体代码如下：

libname mydata 'D:\mydata';

通过这一步骤，SAS能够识别引号中的物理位置，将逻辑库建立在该目录下，同时在以下过程中新建的SAS表格便可以永久储存在该位置，便于反复读取和使用。先运行该代码使其生效。

②利用PROC IMPORT语句导入文件，代码如下：

proc import out= mydata.example
datafile=" D:\mydata\Friedman检验.csv"
dbms=csv replace;
getnames=yes;
run;

该过程在mydata逻辑库中生成example数据集，数据文件由DATAFILE=选项指定，DBMS=选项指定其数据库类型。该案例中初始数据集为csv文件，故而使用“dbms=csv”指定。如果已经存在相同名称的SAS数据集，即可使用REPLACE选项进行覆盖。GERNAMES=YES选项指定从第2行开始读取数据，将数据集的首行变量名作为SAS数据集的变量名。

(二) 适用条件判断(正态性检验)

1. 软件操作

运用UNIVARIATE 过程进行正态性检验，示例代码如下：

proc univariate data= mydata.example plot normal;
var A B C; 
Histogram /normal kernel;
run;

其中“mydata.example”为上一步中导入的数据集名称，“A”、“B”、“C”分别为三组分析变量名，即A、B、C 3种不同频率振动的刺激后受试者反应率(%)。选项PLOT产生了A、B、C 3种不同频率振动的刺激后反应率(%)的平行条状图、箱线图和正态概率图，分别如图2、图3和图4所示。

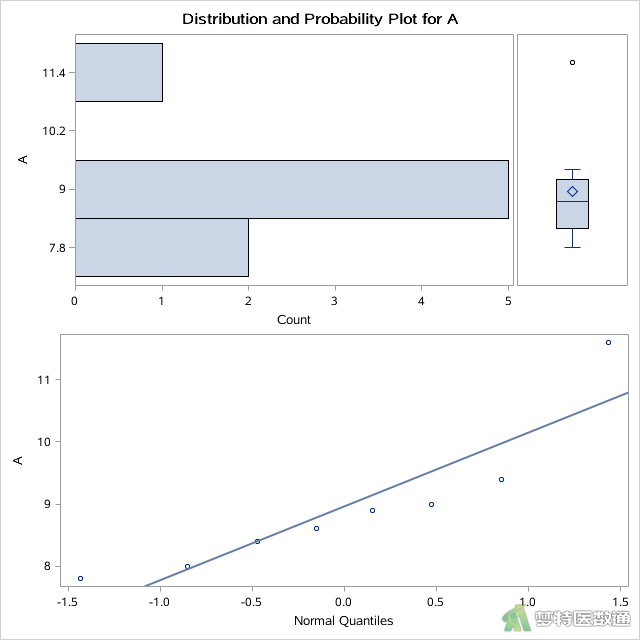
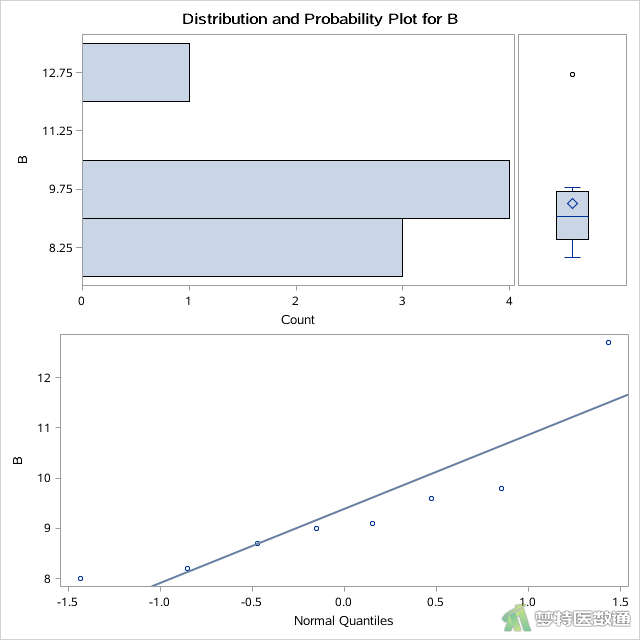
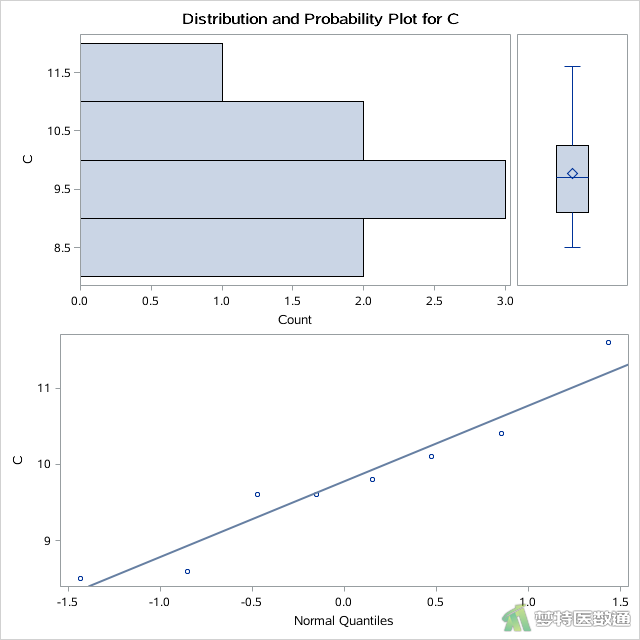
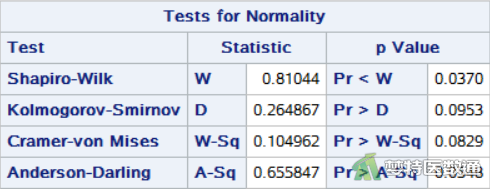
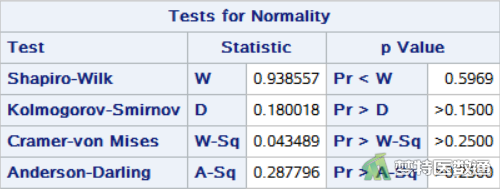
选项NORMAL进行正态性检验，得到A、B、C 3种不同频率振动的刺激后反应率(%)的“Normality Test (正态性检验)”的结果，分别如图5、图6和图7所示。

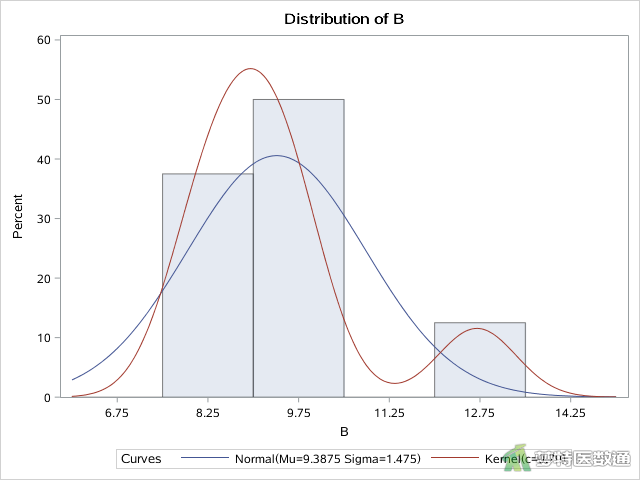
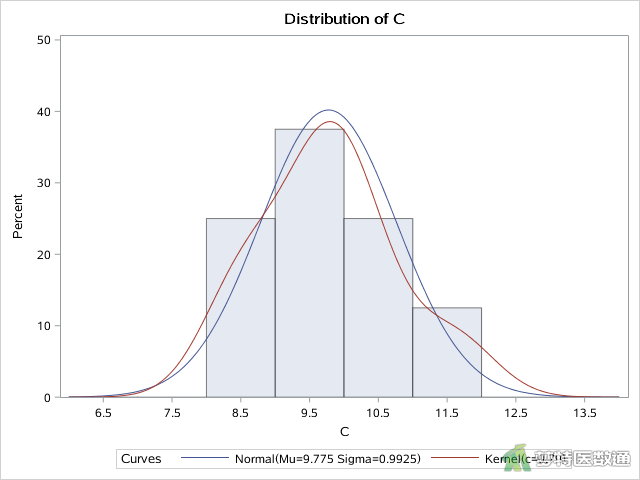
HISTOGRAM语句可以针对指定变量“A”、“B”、“C”分别绘制直方图，该语句中NORMAL选项可作正态分布的密度曲线，而KERNERL选项可作基于数据的核分布密度曲线，可直观展示变量的分布情况，如图8、图9和图10所示。

2.结果解读

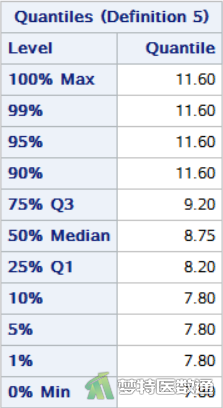
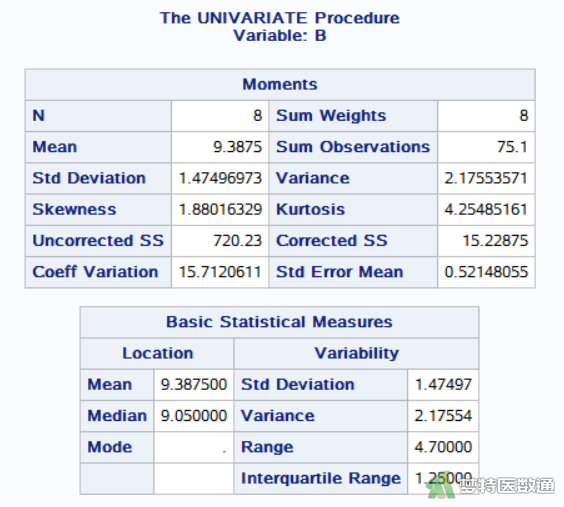
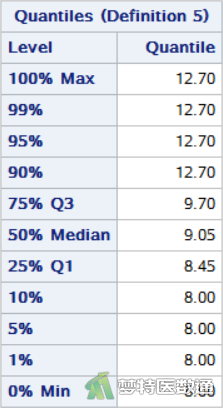
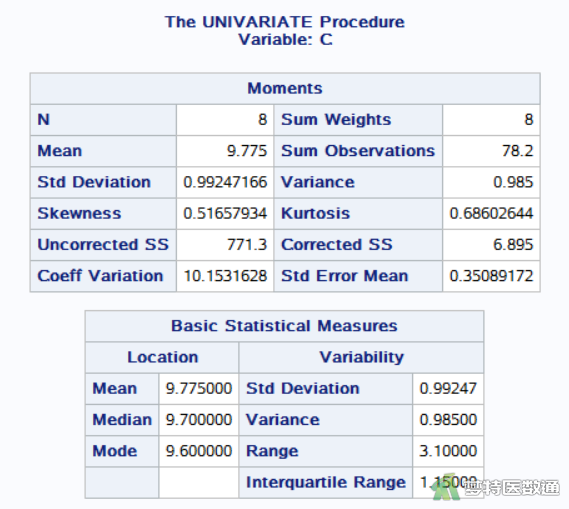
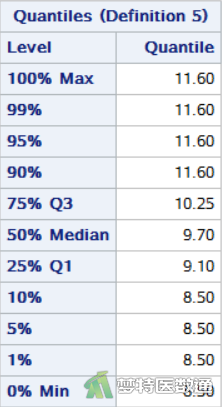
图11-1和图11-2 (变量A)、图12-1和图12-2 (变量B)、图13-1 和图13-2 (变量C) 分别是对三组反应率的统计描述，主要包括三种振动频率下的“N (样本量)”、“Mean(均值)”、“Median(中位数)”、“Std. Deviation(标准差)”、“Min(最小值)”、“Max(最大值)”、“25% Q1(第1四分位数)”、50% Median(中位数)和“75% Q3(第3四分位数)”等指标。可知A、B、C 3种不同频率振动的刺激后反应率(%)的中位数(四分位间距)分别为8.75 (1.00) %、9.05 (1.25) %和9.70 (1.15) %。

注意：计算四分位数间距时，通常将n个变量值从小到大排列。SAS中默认采用基于经验分布函数的平均，计算指数为n*P%=j+g，其中P指的是P百分位数，j为整数部分，g为小数部分，即当g=0时，该P百分位数P_x=(X_j+X_j+1)/2，当g>0时，P_x=X_j+1 (X_j为此数列中的第j个数)。

SPSS中存在计算结果不一致的情况，其原因是SPSS默认的计算方式为，以(n+1)*P%=j+g为计算指数，当g=0时，P_x= X_j，当g>0时，P_x= g*X_j+1+(1-g) X_j。

正态性检验结果如图5、图6和图7所示，分别给出了四种正态性检验的结果，其中较为常用的为Shapiro-Wilk (夏皮罗-威尔克正态性，S-W)检验和Kolmogorov-Smirnov (柯尔莫哥洛夫-斯米诺夫，K-S)检验。K-S检验适用于大样本资料，本案查看S-W检验结果，三组P值分别为0.0599、0.0370和0.5969，A、B两组的P值<0.1，提示这两组数据不服从正态分布。图2、图3和图4分别是三组数据的Q-Q图，可见A、B两组的散点偏离对角线较远，也提示这两组数据不服从正态分布。且图8和图9中两组数据的核分布密度曲线与正态分布密度曲线重合度较低，也可认为A、B两组数据为非正态分布。因此，本案例应使用Friedman检验比较三组反应率的差异。关于正态性检验的注意事项详见文章医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现。

(三) 整体检验

1. 软件操作

①首先对数据进行重新编码，将表格调整为图14所示格式，便于分析。

示例代码如下：

data mydata.analysis;
input ID treatment rate;
cards;
1 1 8.4 
1 2 9.6 
1 3 9.8 
2 1 11.6
2 2 12.7
2 3 11.6
……
7 3 10.4
8 1 7.8
8 2 8.2 
8 3 8.5
;
run;

备注：因篇幅问题，此处省略了部分数据录入

或者使用DO语句进行循环：

data mydata.analysis;
do ID=1 to 8;
 do treatment=1 to 3;
 input rate @@;
 output;
 end;
end;
cards;
8.4 9.6 9.8 11.6 12.7 11.6 9.4 9.1 10.1 9 8.7 9.6 8 8 8.6 8.6 9.8 9.6 8.9 9 10.4 7.8 8.2 8.5
;
run;

该过程中，“treatment”为新建变量，赋值1、2、3，分别代表A、B、C三种不同频率振动的刺激。

②运用FREQ语句进行整体比较，示例代码如下：

proc freq data=mydata.analysis;
table ID* treatment*rate /scores=rank cmh2;
run;

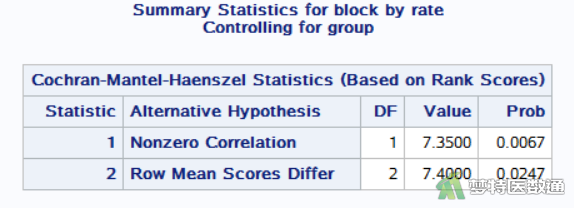
通过“scores=rank”和“cmh2”选项，可以进行“基于秩的Cochran-Mantel-Haenszel检验 (Cochran-Mantel-Haenszel Statistics (Based on Rank Scores))”，其结果如图15所示。

2. 结果解读

(1) 统计描述

由图11-1和图11-2 (变量A)、图12-1和图12-2 (变量B)、图13-1 和图13-2 (变量C)可知A、B、C 3种频率振动刺激的反应率分别为8.75 (1.00) %、9.05 (1.25) %和9.70 (1.15) %。数值存在差异，但还需要依据统计检验的结果进行判断。

(2) 统计学推断

①由FREQ语句得到的图15中结果显示，“行评分均值(Row Mean Scores Differ)”检验结果为χ²=7.400，P= 0.0247，<0.05。拒绝零假设，即3种频率振动刺激的反应率总体比较差别有统计学意义(至少存在两组具有差异)。

(四) 事后检验(两两比较)

虽然得到了“3种频率振动刺激的反应率总体比较差别具有统计学意义”的结论，但若要清楚了解到底是哪些频率刺激的反应率不同，则需要进一步进行两两比较。

1. 软件操作

①可通过如下步骤进行事后检验(两两比较)，首先需要运用RANK步，建立新变量“rank”，表示每个数据的秩次。具体代码如下：

proc rank data=mydata.analysis out=mydata.rank;
var rate;
by ID;
ranks rank;
run;

该过程可新建表格并命名为“mydata.rank”，RANKS语句规定新变量“rank” 表示每个数据的秩次。部分数据如图16所示。

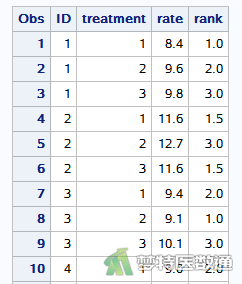
②因为SAS程序中尚不存在直接根据秩次进行两两比较的运算程序，为和SPSS结果保持一致，需通过手动编程的形式，运用排秩后的数据集“mydata.rank”，进一步复现SPSS两两比较的过程和结果。本案例的SAS两两比较程序的理论基础参照SPSS的两两比较方法进行编写。

下面先简单介绍SPSS中两两比较的理论基础：在SPSS中，通过在菜单中选择“All pairwise(全部成对)”，即可通过以下公式计算两两比较的统计量\(T_{jk}\)：

其中\(\bar{R}_{j}\)和 \( \bar{R}_{k}\)分别表示相互比较的各组(treatment)平均秩次，标准误\( \sigma_{e} \)则通过处理组别(treatment)以及组内样本量(n)进行计算，因此本例中g=3，n=8，故\( \sigma_{e} \)=0.5。

计算后的\(T_{jk}\)服从标准正态分布，根据标准正态分布函数计算对应的P值，并使用Bonferroni法调整P值，示例代码如下：

proc sort data=mydata.rank;by treatment;run;/*按照treatment排序*/

proc means data=mydata.rank;/*计算分组平均秩次*/
var rank;
by treatment;
output out=outcome;
run; 

data outcome;
set outcome;
keep treatment _STAT_ rank;
where _STAT_='MEAN';
run;

proc transpose data=outcome out=outcome1;/*数据转置*/
   id treatment;
run;

data outcome2;/*计算两两比较P值和调整后P值*/
set outcome1;
p1=round(2*(1-probnorm(abs(_1-_2)/(sqrt(3*(3+1)/(6*8))))),0.001);
p2=round(2*(1-probnorm(abs(_1-_3)/(sqrt(3*(3+1)/(6*8))))),0.001);
p3=round(2*(1-probnorm(abs(_2-_3)/(sqrt(3*(3+1)/(6*8))))),0.001);
padjust_1=3*p1;
padjust_2=3*p2;
padjust_3=3*p3;
keep p1 p2 p3 padjust_1 padjust_2 padjust_3;
label p1='1 vs 2' p2='1 vs 3' p3='2 vs 3' padjust_1='1 vs 2(调整)' 
padjust_2='1 vs 3(调整)' padjust_3='2 vs 3(调整)';
proc print label;
run;

2. 结果解读

两两比较结果如图17所示：

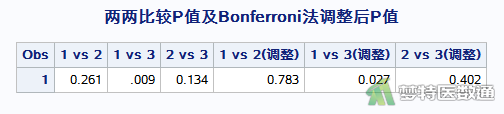
结果显示，本分析共比较了3次，所以Bonferroni法调整后的显著性水平为0.05/3=0.017。表格中“1 vs 2”、 “1 vs 3”、 “2 vs 3”即统计检验的P值，需要和0.017比较，小于0.017则认为差异有统计学意义。此处仅“1 vs 3”：即频率A和频率C比较的P值小于0.017。表格中还显示了“1 vs 2(调整)”、 “1 vs 3(调整)”、 “2 vs 3(调整)”，即调整后P值，该列是将前面P值乘以比较次数得到，可以直接和0.05比较，小于0.05则认为差异有统计学意义。此处仍然是仅“1 vs 3(调整)”：即频率A和频率C刺激反应率比较的P值小于0.05，与“1 vs 3”结果一致，所以认为对频率A和频率C的刺激反应率差异有统计学意义，频率A和频率B、频率B和频率C的刺激反应率差异均无统计学意义。

四、结论

本案例欲比较在A、B、C 3种不同频率振动的刺激下受试者的反应率(%)是否存在差异。通过绘制Q-Q图和Shapiro-Wilk检验，提示数据不服从正态分布，故采用Friedman检验对数据进行分析。

结果显示，受试者对A、B、C 3种不同频率振动的刺激反应率分别为8.75 (1.00) %、9.05 (1.25) %和9.70 (1.15) %，差异有统计学意义(χ²=7.400, P= 0.0247 <0.05)。采用q检验法及Bonferroni法进行两两比较，检验各组显著性水平以0.017和0.05为标准，未调整的P值小于0.017或调整后的P值小于0.05均认为差异有统计学意义。最终两两比较显示，只有频率A和频率C的刺激反应率差异有统计学意义(P=0.009，P调整=0.027)。