前面介绍了Pearson相关性和Spearman等级相关性分析,当两连续变量呈线性关系并满足正态分布时,使用Pearson相关性分析,当变量不满足Pearson相关性分析的适用条件时,使用Spearman等级相关性分析。本篇文章介绍Kendall's tau-b等级相关性分析,主要适用于两变量为有序分类变量的情况。
Kendall's tau相关性分析,是由英国统计学家Maurice Kendall于1938年提出,主要包括Somers' D、Goodman-kruskal's gamma(γ)、Kendall's tau(a、b、c)等一系列相关系数。其中,最常用的是Kendall's tau-b和Kendall's tau-c相关系数。一般认为,tau-b更适合用于即两变量分类数相等,tau-c更适合于两变量分类数不等的情况。本文主要介绍Kendall's tau-b相关性分析。
关键词:相关分析; Kendall相关分析; 肯德尔相关分析; Kendall相关系数; 肯德尔相关系数; 等级相关分析
一、分析思路
两随机变量X、Y,均包含n个数据,则X与Y的对应元素可以构成n个元素对(Xi,Yi),1≤i≤n。如果X与Y呈正相关,那么两个变量有相同的变化趋势,也即X与Y同时增大或同时减小,如(2,3)~(4,6)、(5,2)~(6,3)等,这样变化的对为协和对(concordant pair);如果X与Y呈负相关,那么两个变量有相反的变化趋势,也即X增大Y减小或X减小Y增大,如(2,3)~(3,1)、(5,2)~(4,3)等,这样变化的对为不协和对(disconcordant pair)。如果X与Y至少有一个变量未发生变化,则为不变对,如(2,3)~(2,1)、(5,2)~(4,2)、(2,3)~(2,3)等。
将每一个元素对(Xi,Yi) 与剩余的元素对(Xj,Yj) 进行两两比较,可以获得n(n-1)/2个两两比较的对。Kendall's tau的思路就是,统计在这些两两比较的对中,是协和对多还是不协和对多。如果协和对显著多于不协和对,则为正相关;如果不协和对显著多于协和对,则为负相关;否则两变量不存在相关关系。
Kendall's tau-b相关系数的取值范围为-1到1,相关系数小于0表示两变量负相关,大于0表示正相关,等于0表示两变量相互独立。相关系数的绝对值越大,表示两变量间的相关程度越密切;相关系数越接近于0,表示相关越不密切。
二、适用条件
Kendall's tau-b等级相关性分析,需要满足2个条件:
条件1:两变量是两个连续变量,或两变量是两个有序分类变量,或一个有序分类变量一个连续变量。
条件2:两变量应当是配对的,即来源于同一个个体。
三、统计量计算
(一) Kendall's tau-b相关系数\(\boldsymbol{\tau}_{b}\)
Kendall's tau-b相关系数的计算公式如下:
\(\tau_{b}=\frac{C-D}{\sqrt{T-T_{r}} \sqrt{T-T_{c}}}\)其中:
C是指两两比较对中协和对的个数;
D是指两两比较对中不协和对的个数;
T是指两两比较的总对数,为n(n-1)/2,n为样本量;
Tr是指不变对中,X值不变的个数;
Tc是指不变对中,Y值不变的个数。
(二) 假设检验
1. 建立检验假设,确定检验水准
H0:\(\boldsymbol{\tau}_{b}\) =0,两变量不存在相关关系
H1:\(\boldsymbol{\tau}_{b}\) ≠0,两变量存在相关关系
α = 0.05
2. 计算检验统计量Zb
Zb统计量的计算公式如下:
\(z_{b}=\frac{C-D}{\sqrt{v}}\)其中:
\(v=\frac{v_{0-} v_{r}-v_{c}}{18}+v_{1}+v_{2}\) \(v_{0}=n(n-1)(2 n+5)\) \(v_{r}=\sum_{i=1}^{r} t_{i}\left(t_{i}-1\right)\left(2 t_{i}+5\right)\) \(v_{c}=\sum_{j=1}^{c} t_{j}\left(t_{j}-1\right)\left(2 t_{j}+5\right)\) \(v_{1}=\frac{\sum_{i=1}^{r} t_{i}\left(t_{i}-1\right) \sum_{j=1}^{c} t_{j}\left(t_{j}-1\right)}{2 n(n-1)}\) \(v_{2}=\frac{\sum_{i=1}^{r} t_{i}\left(t_{i}-1\right)\left(t_{i}-2\right) \sum_{j=1}^{c} t_{j}\left(t_{j}-1\right)\left(t_{j}-2\right)}{9 n(n-1)(n-2)}\)上式中:
C是指两两比较对中协和对的个数;
D是指两两比较对中不协和对的个数;
T是指两两比较总对数,为n(n-1)/2,n为样本量;
r是变量X的分类数;
ti是变量X第i分类的个数;
c是变量Y的分类数;tj是变量Y第j分类的个数。
3. 确定P值,作出推断结论
查(标准正态分布界值表),获得P值。
四、案例数据
某社区卫生服务中心欲研究年龄(Age)与冠状动脉粥样硬化等级(Grade)之间的关系,抽样调查了283例年龄≥30岁的居民,收集其年龄和冠状动脉粥样硬化等级数据。年龄按30-39岁、40-49岁、50-59岁、≥60岁统计频数,冠状动脉粥样硬化按照0级、1级、2级、3级统计频数。问冠状动脉粥样硬化等级与年龄是否相关?数据如图1所示。
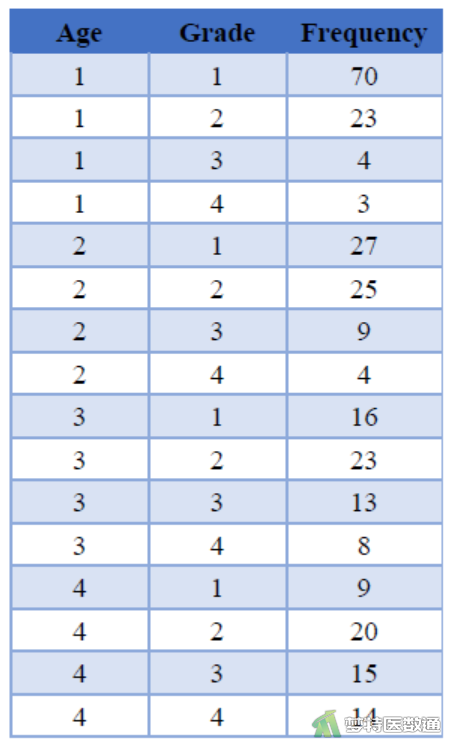
五、案例分析过程
(一) 适用条件判定
本案例中年龄和冠状动脉粥样硬化等级两个变量均为有序分类变量,且属于同一个人,因此满足Kendall's tau-b相关性分析的两个适用条件。
(二) 计算样本相关系数 \(\boldsymbol{\tau}_{b}\)
首先,将原数据转换为图2形式:
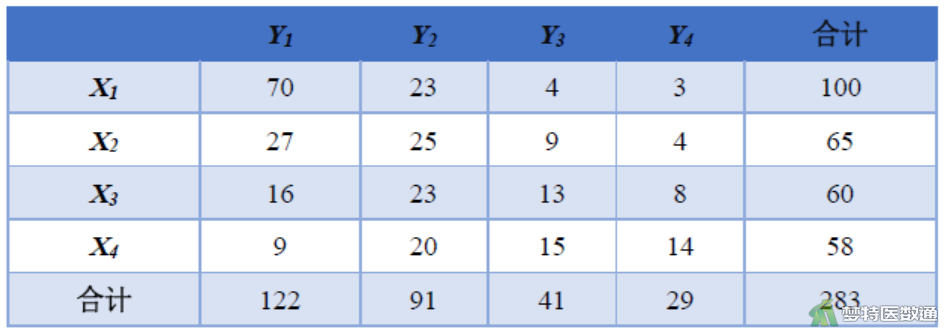
然后,计算协和对的个数C。从(X1,Y1)开始寻找,可发现,正向变化的数据对均在(X1,Y1)的右下方,将(X1,Y1)的频数乘以右下方格子的频数和,即为(X1,Y1)的协和对数。
这样,就可以计算出总的协和对个数:
\(\begin{aligned}C=70 \times(25&+9+4+23+13+8+20+15+14) \\&+23 \times(9+4+13+8+15+14)+4 \times(4+8+14) \\&+27 \times(23+13+8+20+15+14) \\&+25 \times(13+8+15+14)+9 \times(8+14) \\&+16 \times(20+15+14)+23 \times(15+14)+13 \times 14=16315\end{aligned}\)同样地,不协和对的个数D为单元格频数乘以其右上方格子的频数和,如下:
\(\begin{aligned}D=9 \times(23&+13+8+25+9+4+23+4+3) \\&+20 \times(13+8+9+4+4+3)+15 \times(8+4+3) \\&+16 \times(25+9+4+23+4+3)+23 \times(9+4+4+3) \\&+13 \times(4+3)+27 \times(23+4+3)+25 \times(4+3)+9 \times 3 \\&=4704\end{aligned}\)两两比较总对数T为:
\(T=\frac{n(n-1)}{2}=\frac{283 \times 282}{2}=39903\)接下来,求Tr的值,Tr是指不变对中X值不变的个数:
\(T_{r}=\frac{\sum_{i=1}^{r} t_{i}\left(t_{i}-1\right)}{2}=\frac{100 \times 99+65 \times 64+60 \times 59+58 \times 57}{2}=10453\)同样地,
\(T_{c}=\frac{\sum_{j=1}^{c} t_{j}\left(t_{j}-1\right)}{2}=\frac{122 \times 121+91 \times 90+41 \times 40+29 \times 28}{2}=12702\)因此,
\(\tau_{b}=\frac{C-D}{\sqrt{T-T_{r}} \sqrt{T-T_{c}}}=\frac{16315-4704}{\sqrt{39903-10453} \sqrt{39903-12702}}=0.410\)(三) 假设检验
1. 建立检验假设,确定检验水准
H0: \(\boldsymbol{\tau}_{b}\) =0,年龄和冠状动脉粥样硬化等级之间不存在相关关系
H1: \(\boldsymbol{\tau}_{b}\) ≠0,年龄和冠状动脉粥样硬化等级之间存在相关关系
α = 0.05
2. 计算检验统计量Zb
\(v_{0}=n(n-1)(2 n+5)=283 \times 282 \times 571=45569226\) \(\begin{aligned}& v_{z}=\sum_{i=1}^{r} t_{i}\left(t_{i}-1\right)\left(2 t_{i}+5\right) \\=& 100 \times 99 \times 205+65 \times 64 \times 135+60 \times 59 \times 125+58 \times 57 \times 121 \\=& 3433626\end{aligned}\) \( \begin{aligned}& v_{C}=\sum_{j=1}^{c} t_{j}\left(t_{j}-1\right)\left(2 t_{j}+5\right) \\=& 122 \times 121 \times 249+91 \times 90 \times 187+41 \times 40 \times 87+29 \times 28 \times 63 \\=& 5401104\end{aligned}\) \( \begin{aligned}& v_{1}=\frac{\sum_{i=1}^{r} t_{i}\left(t_{i}-1\right) \sum_{j=1}^{c} t_{j}\left(t_{j}-1\right)}{2 n(n-1)} \\=& \frac{(100 \times 99+65 \times 64+60 \times 59+58 \times 57) \times(122 \times 121+91 \times 90+41 \times 40+29 \times 28)}{2 \times 283 \times 282} \\=& 3327.4191\end{aligned}\) \( \begin{aligned}& v_{2}=\frac{\sum_{i=1}^{r} t_{i}\left(t_{i}-1\right)\left(t_{i}-2\right) \sum_{j=1}^{c} t_{j}\left(t_{j}-1\right)\left(t_{j}-2\right)}{9 n(n-1)(n-2)} \\=& \frac{(100 \times 99 \times 98+65 \times 64 \times 63+60 \times 59 \times 58+58 \times 57 \times 56) \times(122 \times 121 \times 120+91 \times 90 \times 89+41 \times 40 \times 39+29 \times 28 \times 27)}{9 \times 283 \times 282 \times 281} \\=& 20793.678\end{aligned}\) \( \begin{aligned}& v=\frac{v_{0}-v_{r}-v_{c}}{18}+v_{1}+v_{2} \\=& \frac{45569226-3433626-5401104}{18}+3327.4191+20793.678 \\=& 2064926.43\end{aligned}\) \( Z_{k}=\frac{C-D}{\sqrt{v}}=\frac{16315-4704}{\sqrt{2064926.43}}=8.080\)3. 确定P值,作出推断结论
Zb =8.080,查(标准正态分布界值表),P<0.001。按α = 0.05水准,拒绝H0,接受H1,即年龄和冠状动脉粥样硬化等级之间存在相关关系。
(四) 结论
年龄和冠状动脉粥样硬化等级呈正相关,\(\boldsymbol{\tau}_{b}\) =0.410,P<0.001。