两步聚类(Two-step clustering)是近年来发展起来的智能聚类方法,是一种探索性的样品聚类方法。其基本思想是先进行预聚类,然后在预聚类基础上,根据AIC和BIC最小原则,自动判定聚类数据。两步聚类的聚类变量既可以是连续性的计量资料,也可以是离散性的计数资料,并且自动确定进行聚类的类别数,结果稳健可靠,可用于解决海量数据、复杂结果的聚类分析问题。
关键词:SPSS; 聚类分析; 快速聚类; K-均值聚类; 系统聚类; 两步聚类
一、案例介绍
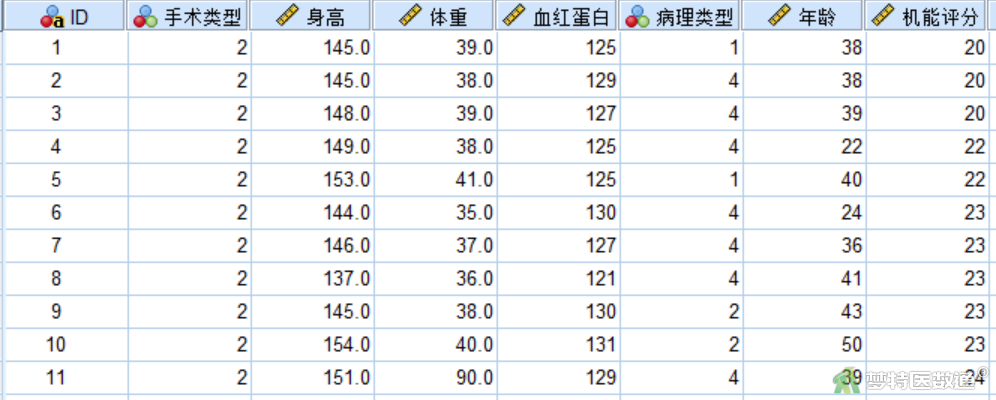
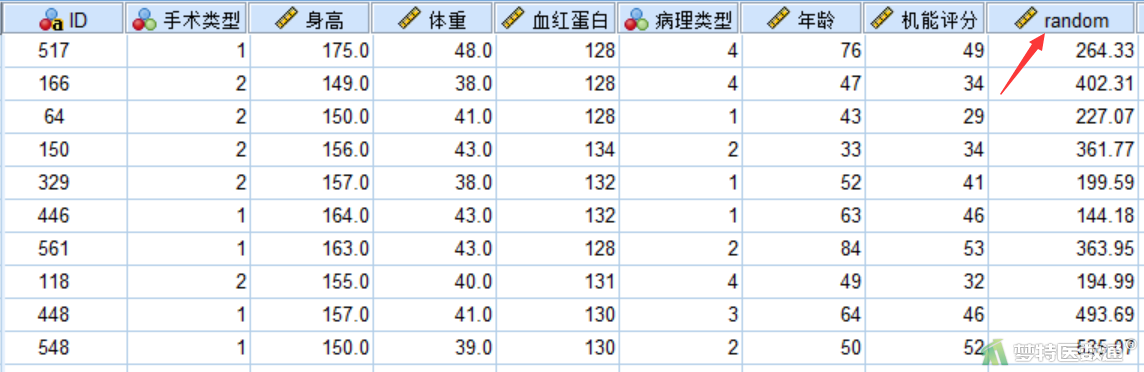
研究者跟踪调查某医院肿瘤科的580名患者,测得手术类型、身高、体重、血红蛋白、病理类型、年龄和机能评分等7个指标。试用合适的聚类方法对580名患者进行归类并解释结果。部分数据见图1,本案例数据可从“附件下载”处下载。
二、问题分析
本例研究样本量为580,研究指标包括分类变量(手术类型、病理类型)和连续性变量(身高、体重、血红蛋白、年龄和机能评分),研究指标中同时包含分类变量和连续性变量等2种不同变量类型,因此本例采用两步聚类法进行分析。
三、软件操作及结果解读
(一) 样品随机化处理
两步聚类的分类特征数和最终聚类结果均与样品的排列顺序有关,在进行聚类分析前,最好对样品进行随机化处理。
1. 软件操作
选择“转换”—“随机数生成器”(图2)。
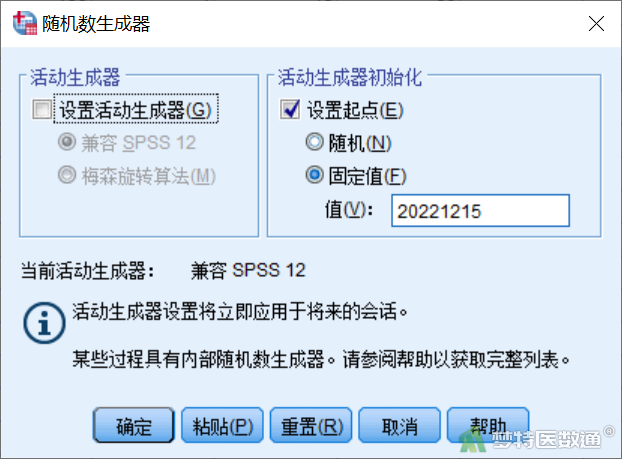
在“随机数生成器”对话框中勾选“设置起点”,在固定值中输入数字方便结果复现,如输入“20221215”(图3)。
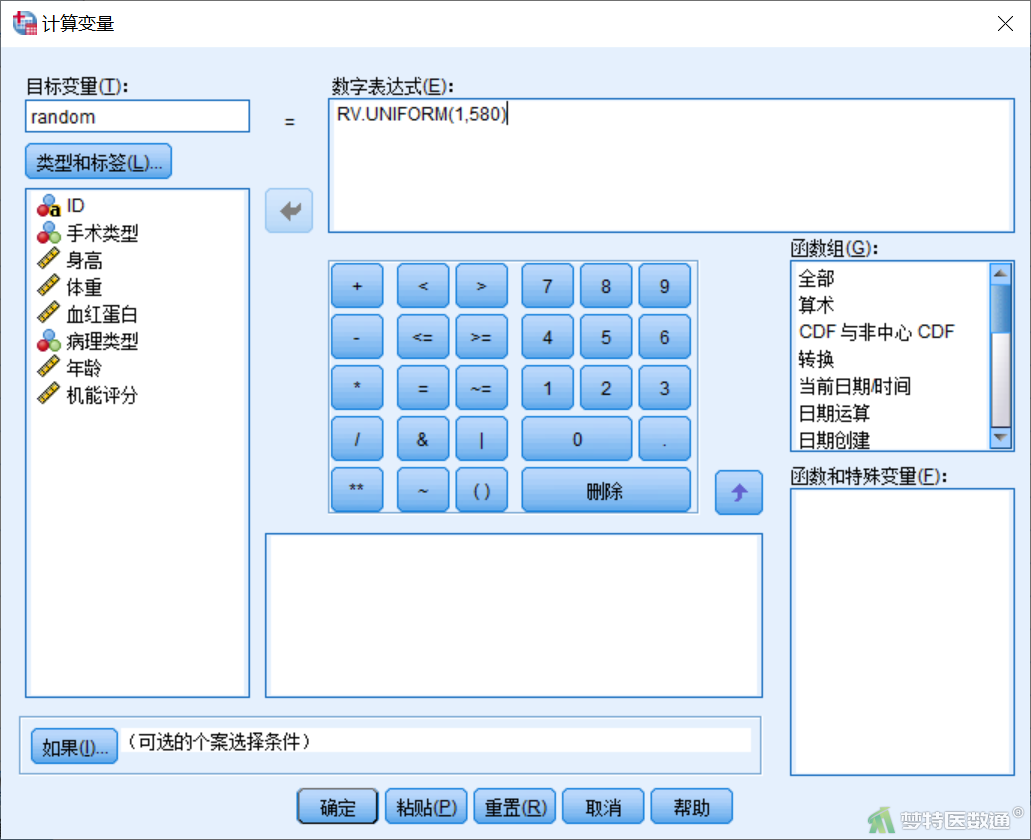
选择“转换”—“计算变量”,在“计算变量”对话框中的“目标变量”中输入随机数字变量名称“random”,在“数字表达式”中输入“RV.UNIFORM(1,580)”,点击“确定”(图4),即可在数据视图生成一列新的变量“random”(图5)。
在聚类分析前,先对随机数排序。点击“数据”—“个案排序”,在“个案排序”对话框中,将“random”选入“排序依据”,排列顺序保持默认(图6)。
(二) 两步聚类分析
1. 软件操作
选择“分析”—“分类”—“二阶聚类”(图7)。
在“二阶聚类分析”对话框中按以下参数设置相应选项(图8):
1) 将连续变量和分类变量分别选入相应的对话框,即将“手术类型”和“病理类型”两个变量放入“分类变量”框中,将变量“身高”、“体重”、“血红蛋白”、“年龄”和“机能评分”等5个变量放入“连续变量”框中,其他保持默认状态。
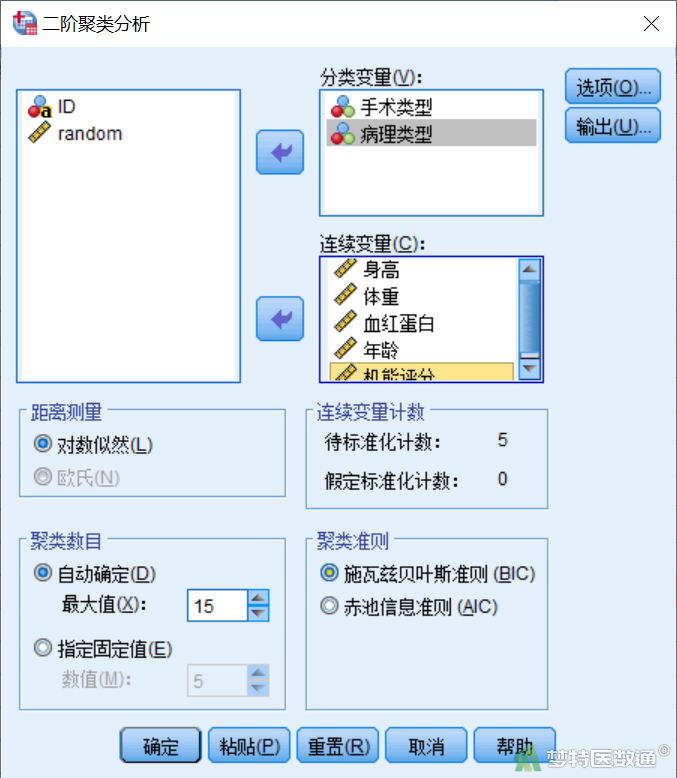
2) 距离测量:如果只对连续性变量进行聚类,距离测量既可以使用“对数似然值(L)”,也可以使用“欧几里得(Euclidean)”;如果进行聚类分析时还有分类变量,距离度量则就只能用“对数似然值(L)”,本例选择“对数似然值(L)”。
3) 聚类数目:聚类数必须是整数,不能小于2,且不能大于观察例数,本例保持默认状态,自动确定,最大值“15”。
4) 选项:用于设置对于连续性变量进行标准化,软件可自动进行,无需设置(图9)。
5) 输出:可以选择存储聚类结果为新变量,或者导出模型/CF树为XML文件,供进一步分析使用,本例勾选“透视表”、“图表和表(在模型查看器中)”和“创建聚类成员变量”,“创建聚类成员变量”将生成一个新变量,表示每一个观察单位的所属类别,其他保持默认状态(图10)。
2. 结果解读
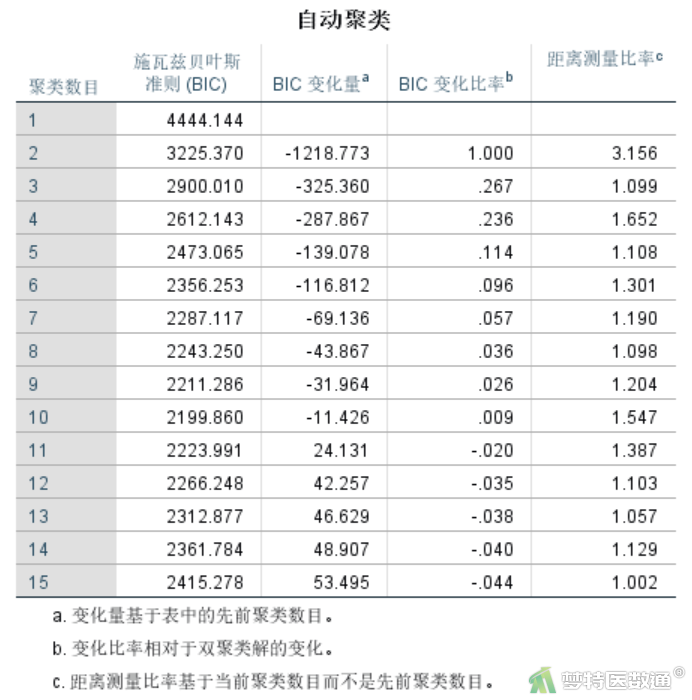
自动聚类结果(图11)展示了各聚类个数对应的BIC、BIC变化量、BIC变化比率和距离测量比率。
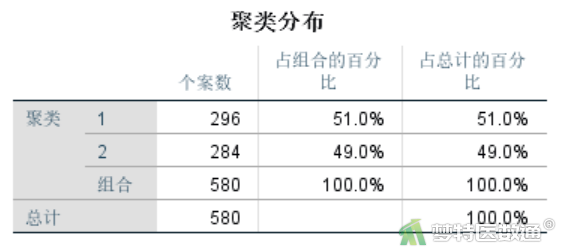
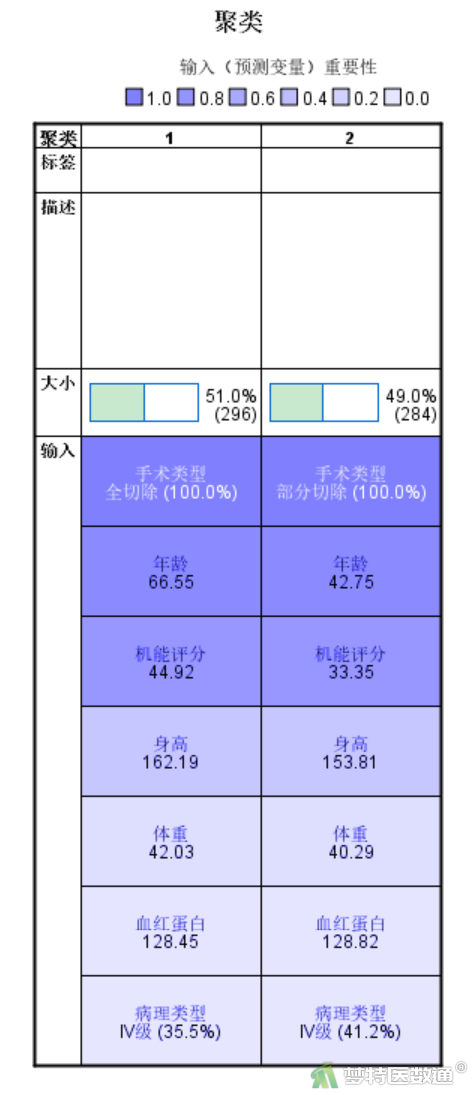
聚类分布结果(图12)显示本案例聚为2类,每类的个数分别为296和284。聚类概要和频率结果(图13)中,列出了每个连续性变量在各类中的均数和标准差,以及分类变量在各类中的频数和百分比。
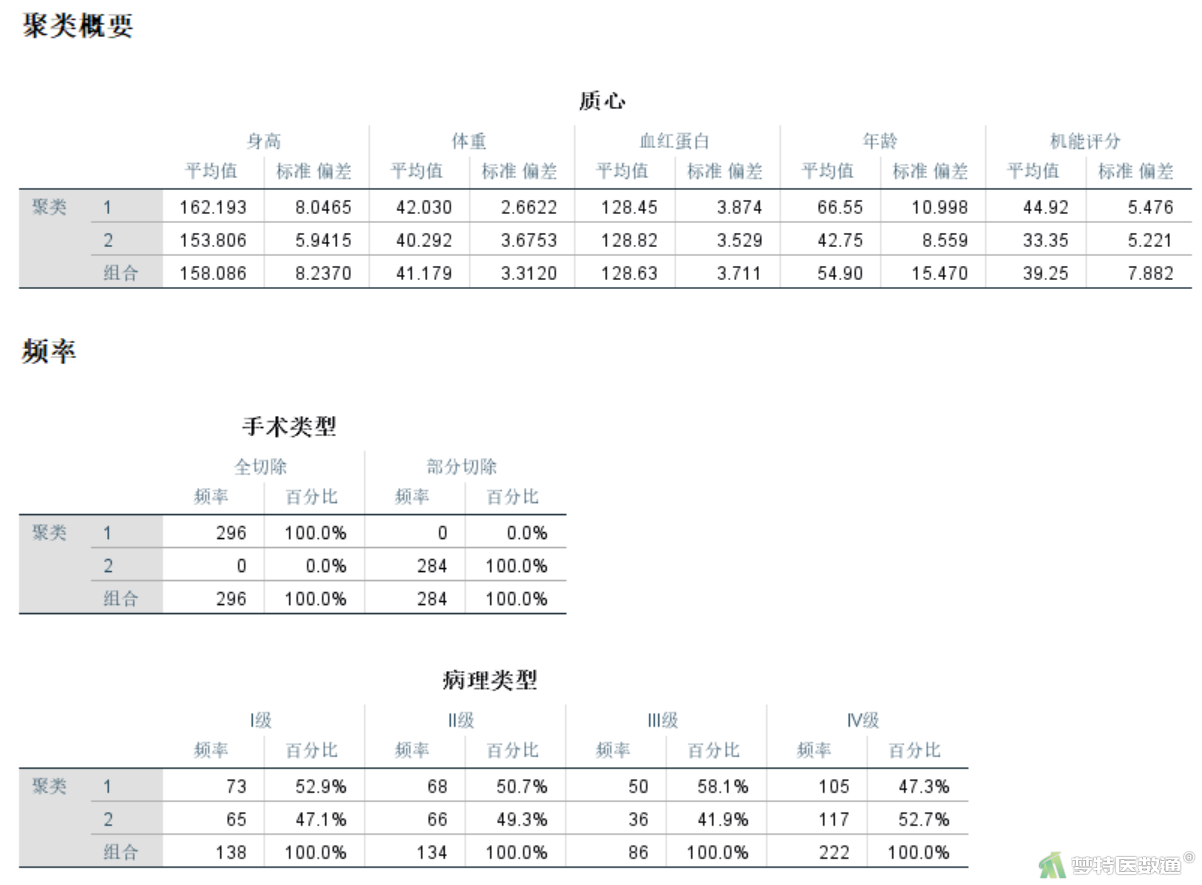
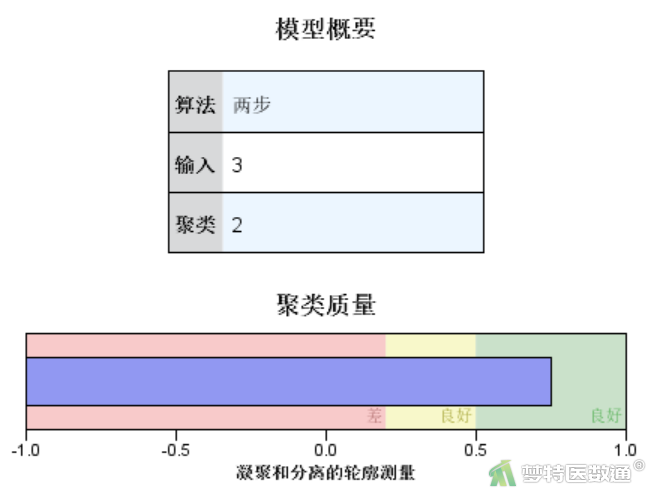
模型概要(图14)表示本例采用两步聚类算法,输入变量为7个,结果聚成2类。聚类质量(图14)中列出了聚类结合和分离的Silhouette测度,可据此判断聚类效果,其值越大效果越好。根据聚类质量结果可快速检查聚类结果,如果较差,可以返回主对话框修改模型设置。本例聚类效果为“良好”,其第二个“良好”为误译,应该为“优秀(Good)”。
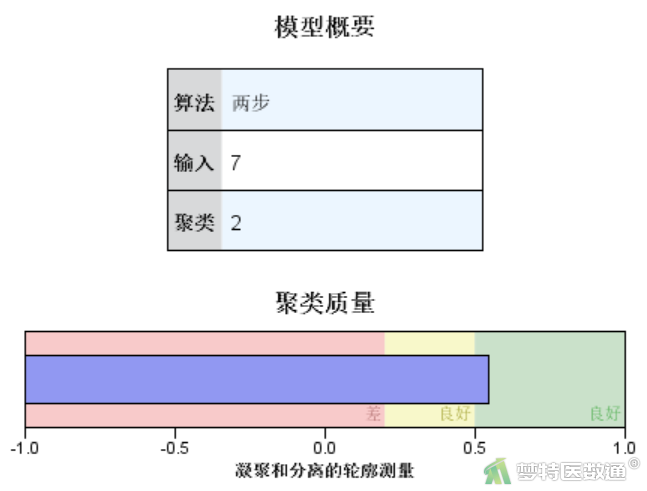
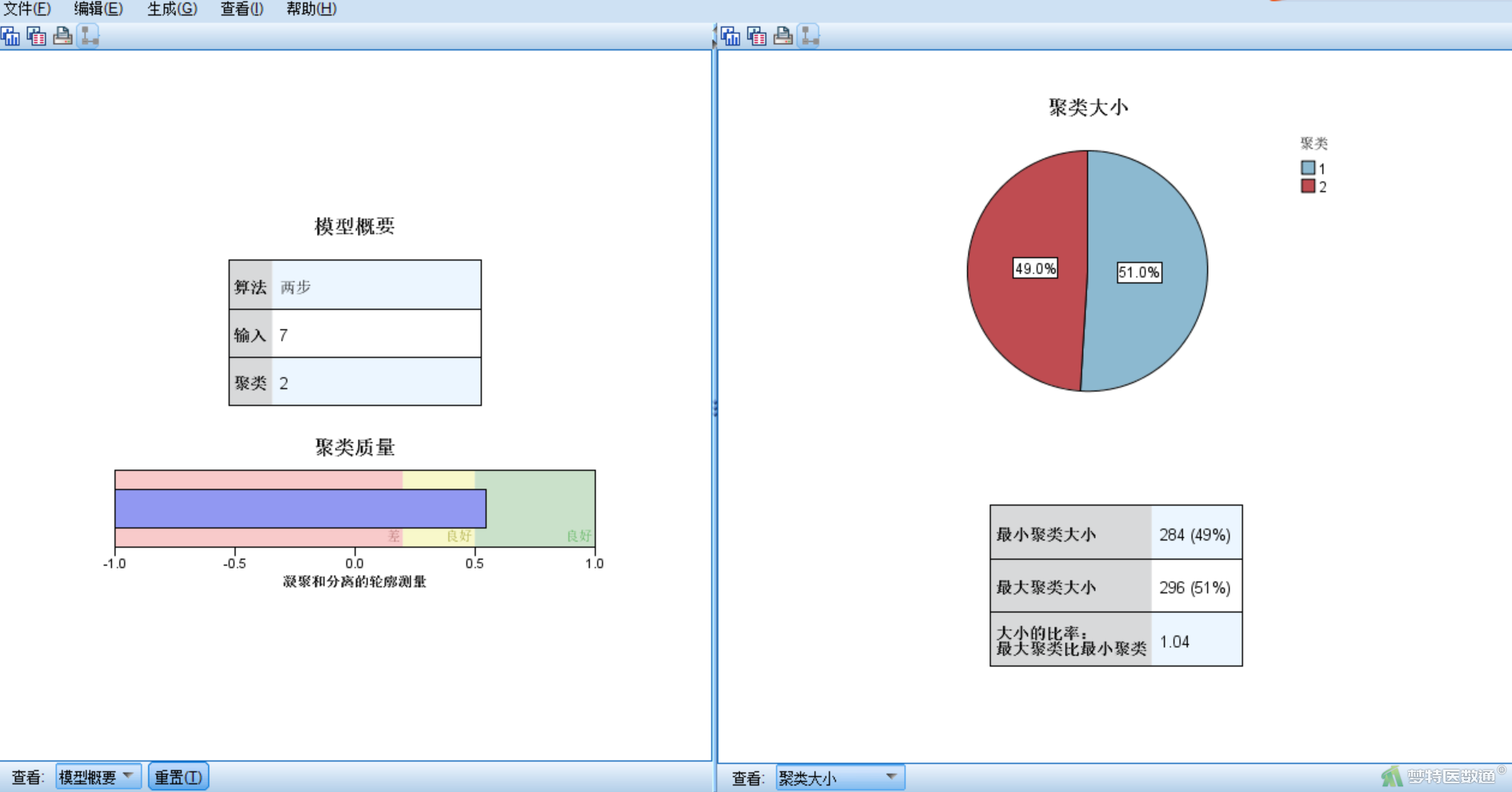
双击模型摘要(图14),可展开模型查看器(图15),左侧为主视图(默认为模型摘要和聚类质量),右侧为辅助视图(默认为聚类大小)。
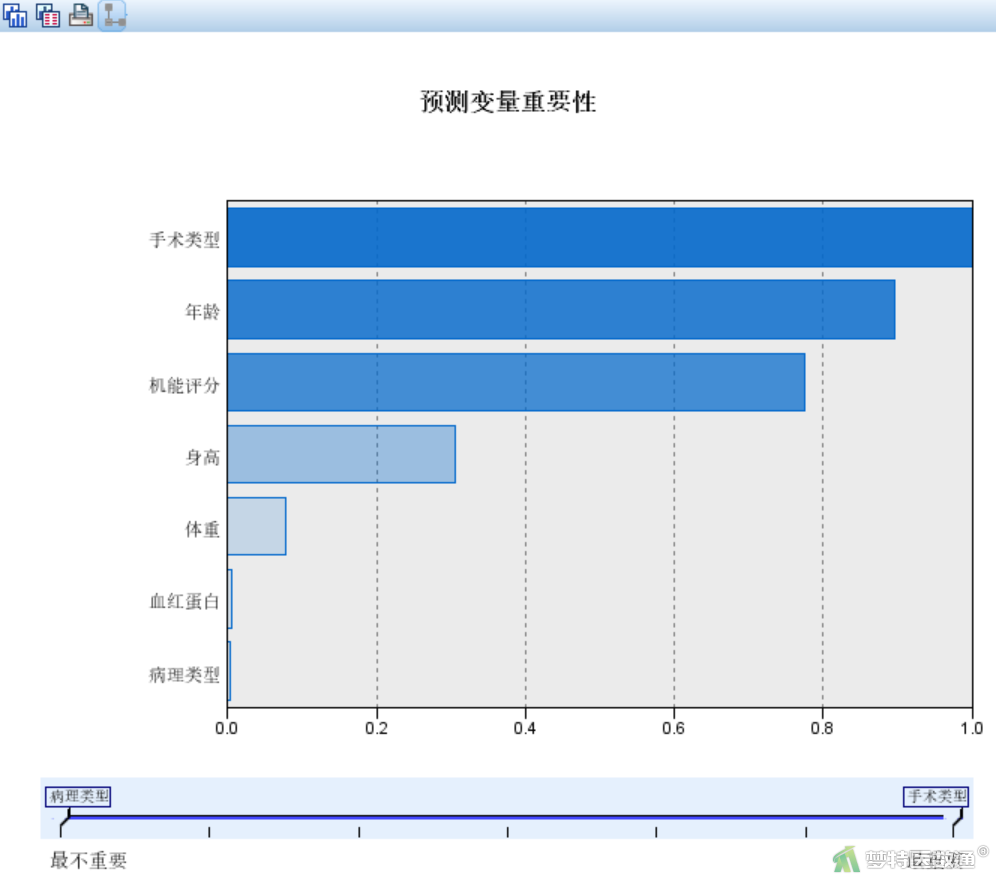
点击模型查看器窗口(图15)右下角下拉菜单,选择“预测变量重要性”,可显示在输入7个自变量中,对于最终建立的2个聚类,按变量的重要性大小排序(图16),结果可见,手术类型>年龄>机能评分>身高>体重>血红蛋白>病理类型。对于重要性比较低的变量可以考虑剔除,再重新进行聚类分析。
将模型查看器窗口(图15)左侧底部选项卡更改为“聚类”,可显示最终聚成2类中各个指标的分布(图17),分布差异越大,说明该指标的重要性越高。同时聚类模型概要中颜色的深浅也可表示各个变量在聚类分析中的重要性,对于本例而言,手术类型的重要性最高,病理类型的重要性最低。
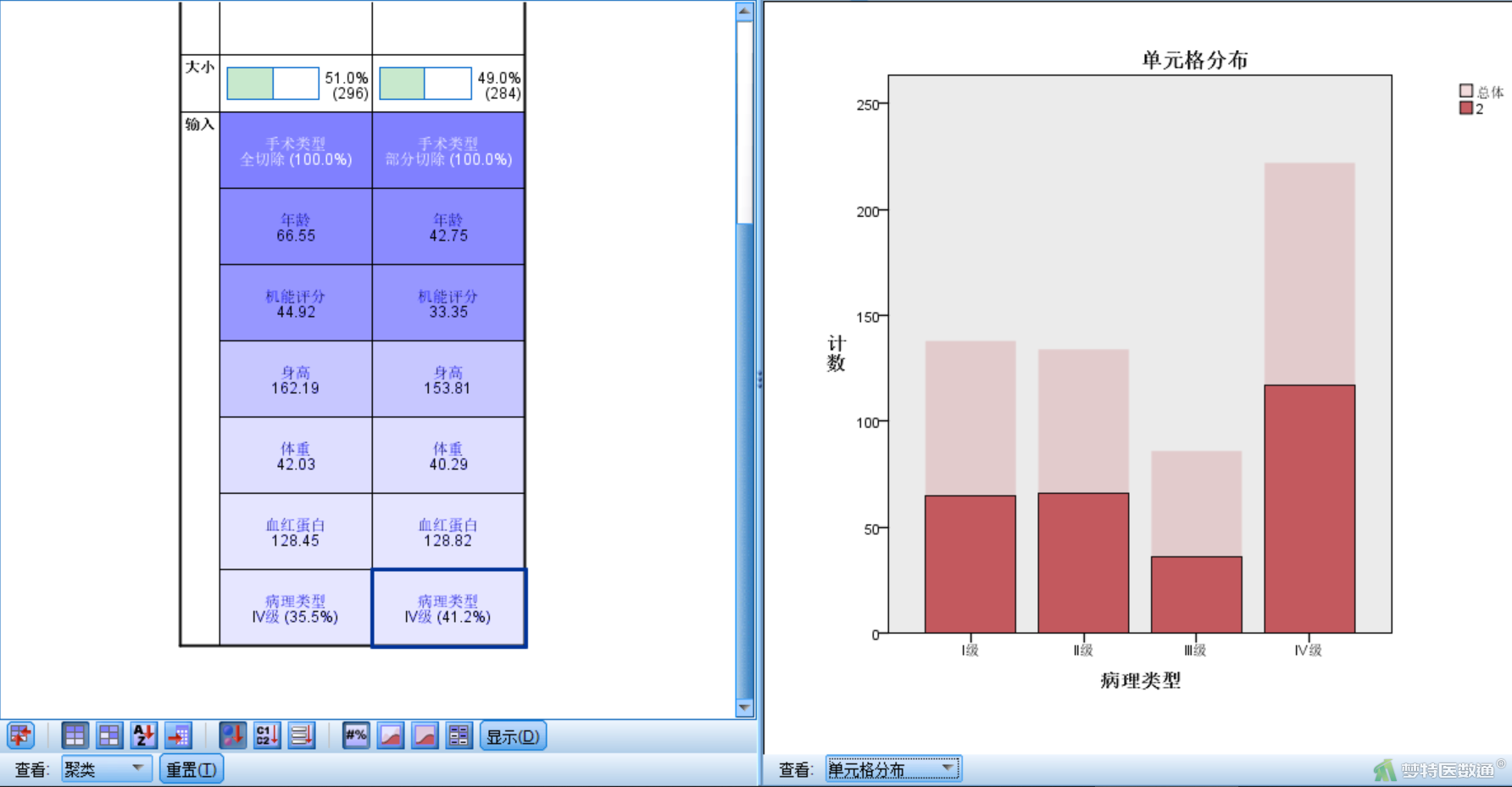
在模型查看器窗口(图15)右下侧选项卡更改为“单元格分布”,任意选中左侧的变量可以查看该变量各水平在各个类别中的分布情况。如图18为病理类型的各水平在各类别中的分布情况。
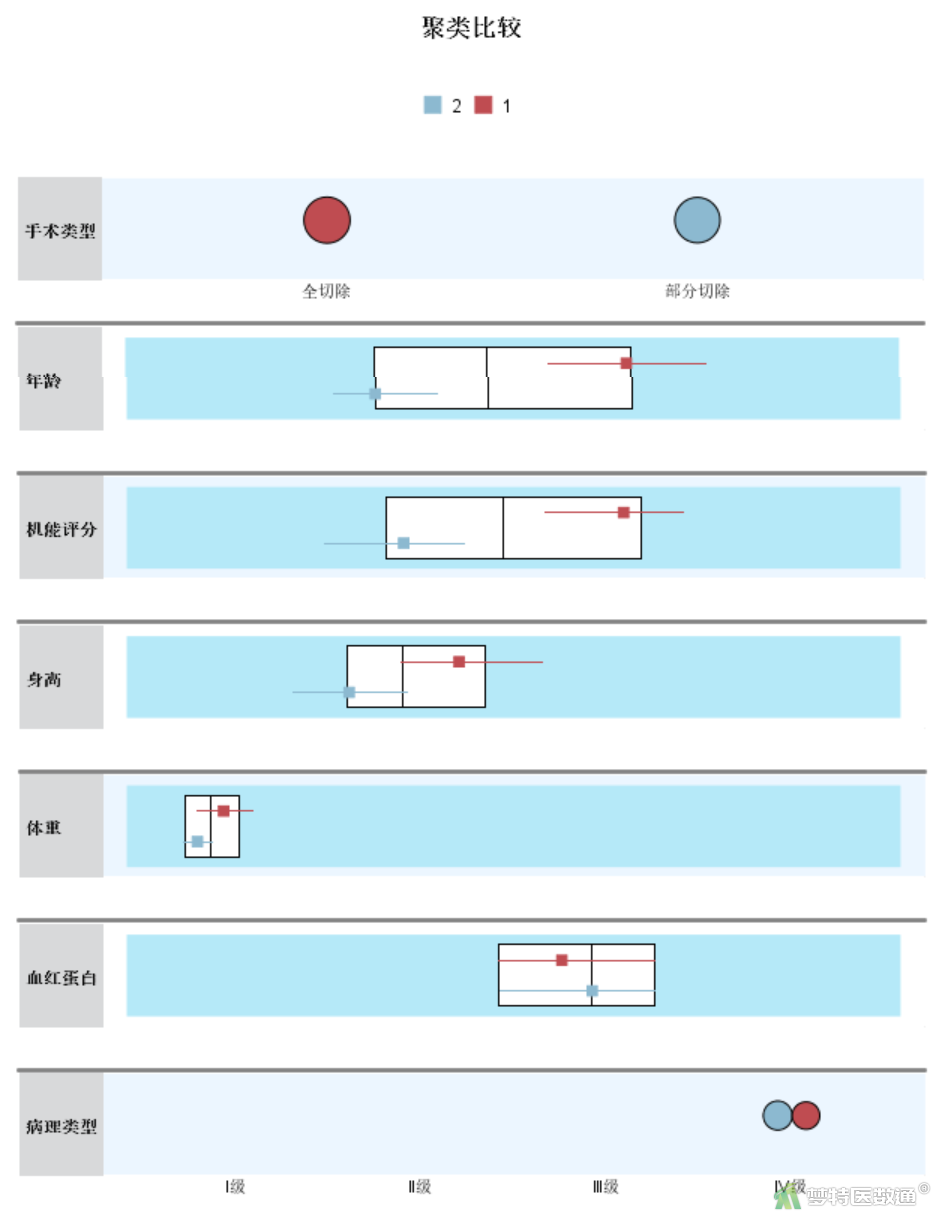
在“模型查看器”窗口(图15)右下侧选项卡更改为“聚类比较”,左侧主视图选择2列变量,可直观表达每个变量在2个类别中的重要性和特点(图19)。分类变量用圆点表示,连续性变量用箱图表示。如手术类型中,全切除在第一类中比较重要,部分切除在第二类中比较重要;年龄在第一类中的长度比第二类长,表示在第一类中更重要。
四、模型优化
通过上述分析发现手术类型、年龄、机能评分3个变量最为重要,再以这3个模型进行两步聚类,发现其效果稍微优于7个变量的聚类结果(图20),但是删减了4个变量显然会节省不少成本。
五、结论
本案例通过两步聚类分析,580名患者被聚类成2类。其中第1类患者296例,占51.0%,他们全部为手术全切除型患者,其平均年龄、机能评分相对较高;第2类患者284例,占49.0%,他们全部为部分切除型患者,其平均年龄、机能评分相对较低。
六、知识小贴士
聚类效果的判断基于Kaufman和Rousseeuw提出的关于聚类结果解释的标准:分为Good (优秀)、Fair (良好)、Poor (较差)三类。Silhouette测度定义为:(B-A)/max(A, B),其中A代表个体观测值距所述类别类中心的距离,B代表个体观测值距其他最近类中心的距离。
Silhouette系数为1表示所有个体均位于其所属类别的类中心上;-1表示所有个体均位于其他类别的类中心上;0表示个体距自身类中心的距离与距其他类中心的距离相等。
七、分析小技巧
如两步聚类分析结果显示聚类质量差时,可结合研究目的和专业背景,对纳入的变量进行适当删除来优化模型。