系统聚类(Hierarchical clustering)也称层次聚类或分层聚类,不仅可以对变量聚类,还可以对样品进行聚类。本文将实例演示在SPSS软件中实现系统聚类分析的过程。
关键词:SPSS; 聚类分析; 快速聚类; K-均值聚类; 系统聚类; 两步聚类
系统聚类的过程是先将n个样品或变量当成n个分类,然后将距离接近(样品聚类)或性质接近(变量聚类)的两类合并为一类,再从n-1类中继续寻找最接近的两类合并为一类,最终将所有类别合并为一类。系统聚类既可适用于连续变量,也可适用于分类变量。
一、案例介绍
某研究为评价中学一年级语文、数学、英语、物理、历史、政治、地理和音乐8门科目学习的重要性,调查了289名家长对各科重要性进行评分。请根据评分的差异将各科目进行适当分类,并对结果加以分析。部分数据见图1,本案例数据可从“附件下载”处下载。
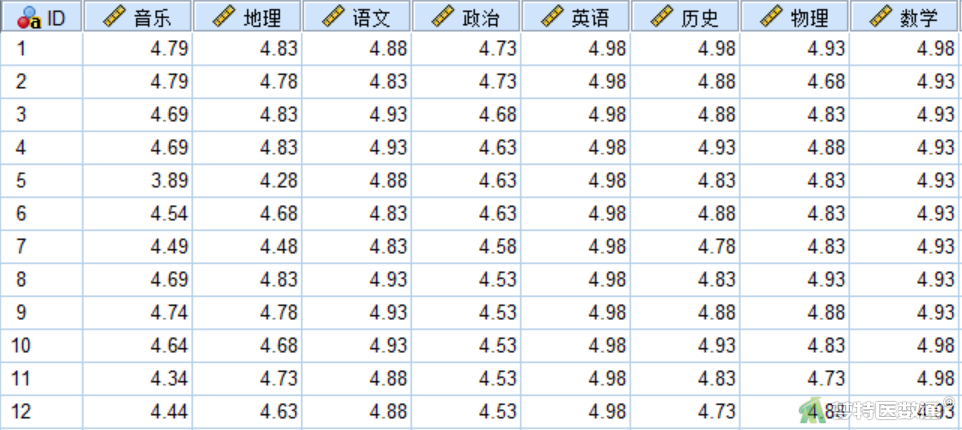
二、问题分析
该研究的主要目的是根据家长对中学一年级各科学习重要性的评价对各科目进行分类,本例样本量为289,聚类的变量为8,在系统聚类条件范围内,因此采用系统聚类分析方法。
三、软件操作及结果解读
(一) 统计学描述
1.软件操作
先对数据进行统计学描述,了解其大致情况。点击“分析”—“描述统计”—“描述”,将8个变量选入右侧“变量”框,点击“确定”(图2)。
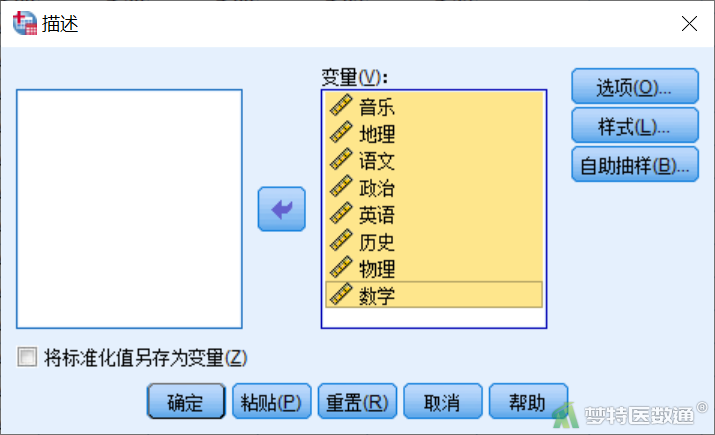
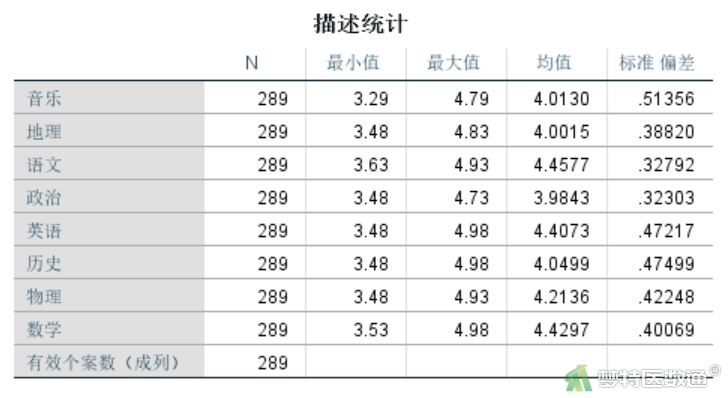
2 结果解读
“描述统计”结果(图3)显示,家长对8门科目打分平均值都在4分左右,标准差也都在0.30~0.52之间,由此可见各科得分较为一致。
同时,需要理清在聚类中需重点考虑的问题,在本例中各科目得分是否有明显差异是分析中需要重点回答的问题。此外,8门科目从分类上可分为主课、专业课程(文科课程、理科课程)和艺术类课程,各类课程在学生考评中占比不同,这将直接影响到家长的评分。
(二)系统聚类分析
1. 软件操作
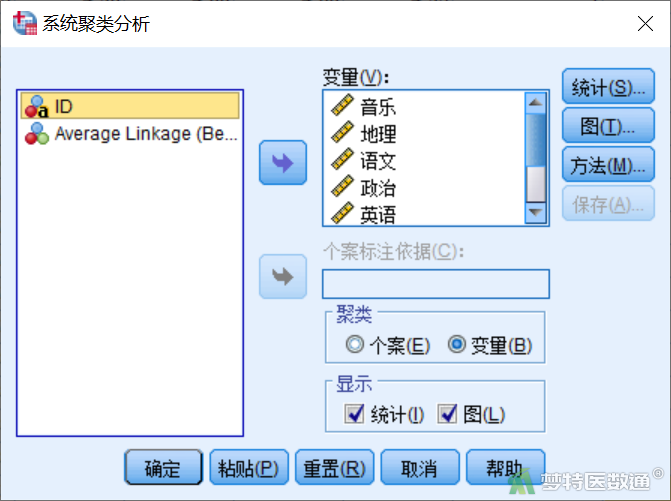
选择“分析”—“分类”—“系统聚类”,打开系统聚类分析对话框(图4)。
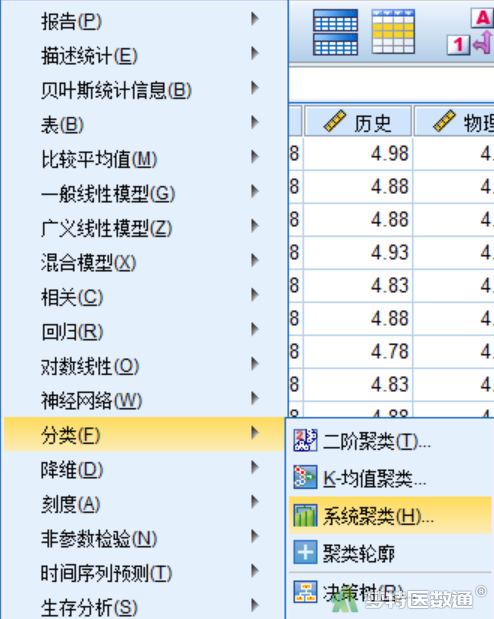
在“系统聚类分析”对话框中按以下参数设置相应选项:
1) 将“语文”“数学”“英语”“物理”“历史”“政治”“地理”和“音乐”放入变量框中。本例是对变量进行分类,故聚类选择“变量”聚类,其他保持默认选择状态(图5)。
2) 统计量:点击“统计量”,打开“系统聚类分析:统计量”对话框,聚类成员选择“单一方案”,并输入“3”(图6)。绝大多数情况我们不知道应该聚成几类,一般输入3~5类,软件自动进行聚类,然后结合专业进行解释。

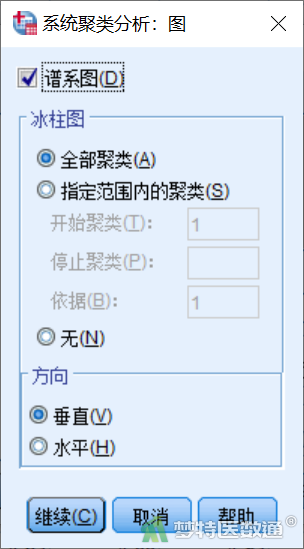
3) 图:点击“图”,打开“系统聚类分析:图”对话框,勾选“树状图”。
树状图可以做树状结构图,是观察和理解聚类结果的重要图形,且只有系统聚类可以做;“冰柱图”虽然也是观察聚类结果的一类图形,但是在应用和可读性方面均较“谱系图”差一些;“方向”表示图形呈现形式,本例选择“垂直”(图7)。
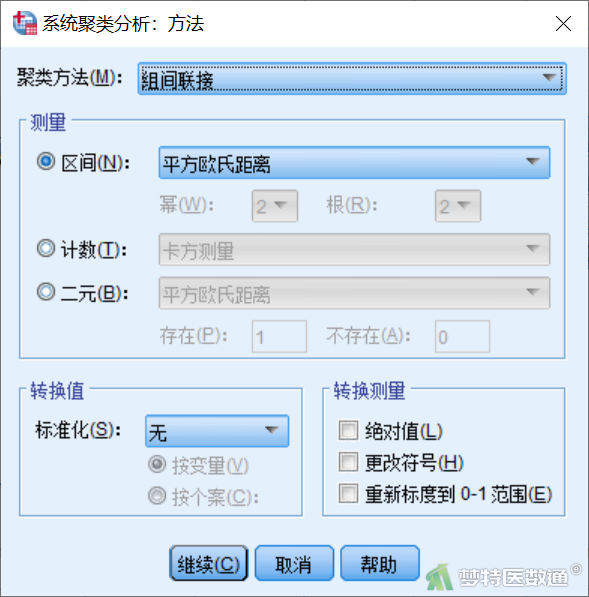
4) 方法:点击“方法”,打开“系统聚类分析:方法”对话框 (图8)。“聚类方法”下拉列表中选择更为常用的组间联接法,它是一种稳健的方法,在大多数情况下表现优异。系统聚类适用的指标类型包括计量变量、数值变量等区间性的连续资料,计数资料及二分类资料。
“转换值”下拉列表可设置按照Z值、全距、平均值或标准差限定等方式进行标准化,也可以设定按照案例还是按照变量方向进行标准化;“转换度量”可用来设置进一步的转换方法,包括绝对值变换、更改符号变换和重新标度到0-1范围转换等3种方式,但实际数据分析过程中一般不需要对“距离”、“转换值”和“转换度量”这些选项进行设置,保持默认选择即可,如需改进聚类效果,可在此处“方法”上进行调整和选择。
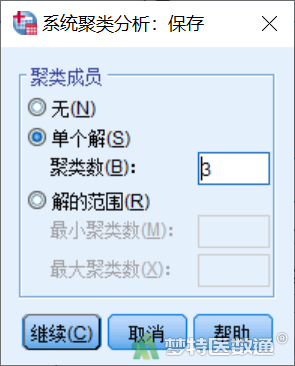
5) 保存设置:点击“保存”,打开“系统聚类分析:保存”对话框(图9),本例前面已选择聚成3类,因此选择单个方案,输入数目“3”。点击“继续”后,点击“确定”。
2. 结果解读
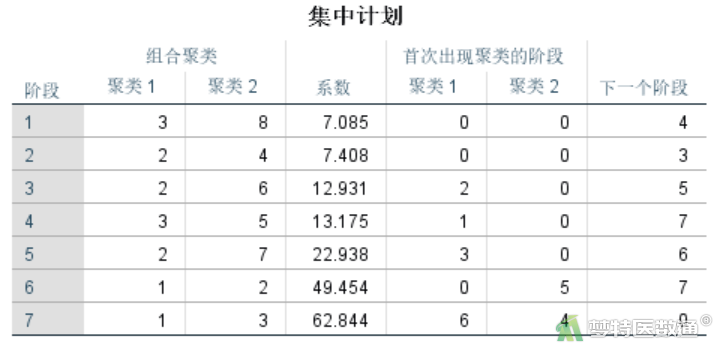
集中计划结果(图10)反映聚类的过程,“组合聚类”列出了在某一步中哪些对象会参与合并,如:第一步是变量3和变量8合并,第二步是变量2和变量4合并,以此类推,直到所有8个变量被全部合并为一类。“系数”列给出了每一步的聚类系数,该数值表示被合并的两个类别之间的距离大小,本例中是按照组间联接法计算出的两类间欧几里得平方距离的平均值。“首次出现聚类的阶段”列表示参与合并的类别最早是在第几步中出现的,0代表该对象是第一次出现在聚类过程中。“下一个阶段”列表示在这一步中合并的类别,下一步将在第几步中再与其他类别进行合并。
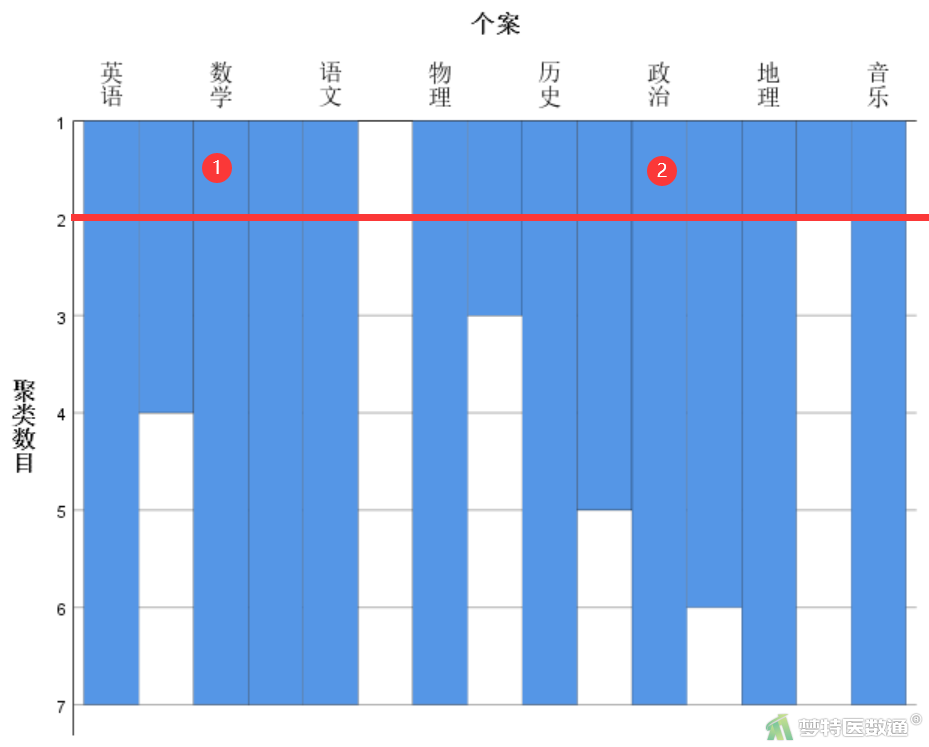
冰柱图(图11)中,以图中所作的横线为例,横线对应的聚类数目为2,该横线将中学一年级的8门科目划分为2个部分。
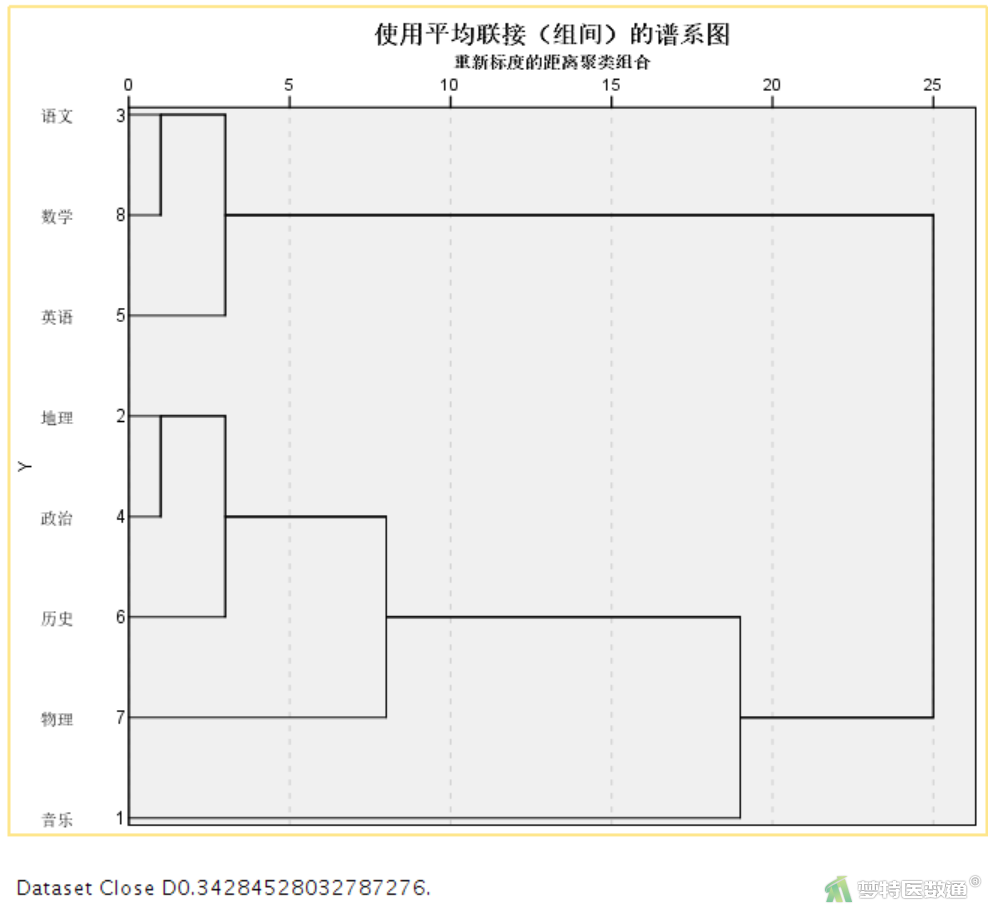
谱系图(图12)可更加形象地展示聚类的结果,本例中发现音乐首先被单独划分出来,可见艺术类课程和专业课程的重要性不同,其他7门专业课程被分为2组,语文、数学、英语是一组,地理、政治、历史和物理则被分在另一组,而其中的物理的距离又稍微远一些。以上为初步聚类结果,下面还需要进一步考虑这一分析的合理性。首先艺术类课程和专业类课程最早被区分开来较合理(考试所需),其次,语文、数学和英语分在一组,这三门课程是中学阶段的主课(可能考试分数比较高),被划分为一组也比较合理;同时,物理的距离又相对远一点,因为地理、政治、历史均为文科科目,而物理科目为理科科目,所以出现当前结果是合理的。综上所述,本例科目的划分是合理的。
四、结论
该案例为系统聚类分析,通过对中学一年级语文、数学、英语、物理、历史、政治、地理和音乐等8门科目学习的家长评分重要性的差异进行分类,最终聚类形成3类,音乐课程单独形成一类,即“文艺课程类”,语文、数学和英语形成一类,即“主课程类”,历史、政治、地理和物理形成一类,即“专业课程类”。
五、分析小技巧
针对聚类分析结果,需要综合考虑分析结果的合理性,如结果中存在不合理之处,可以在系统聚类“方法”选项卡中调整分析选项,改进聚类结果。