在前面文章中介绍了单因素重复测量方差分析(One-Way Repeated Measures ANOVA)的假设检验理论，本篇文章将实例演示在SPSS软件中实现单因素重复测量方差分析的操作步骤。
关键词: GraphPad Prism; 纵列表; 重复测量设计; 重复测量单因素方差分析
一、案例介绍
检验科研究血样放置时间对某生化指标浓度检测的影响，采集了10份人体血液标本，分别在放置0分钟(T0)、30分钟(T30)、60分钟(T60)和90分钟(T90)时对该指标的浓度(mmol/L)进行检测，分析放置时间是否对该生化指标检测结果有影响？数据见图1。本案例数据可从“附件下载”处下载。
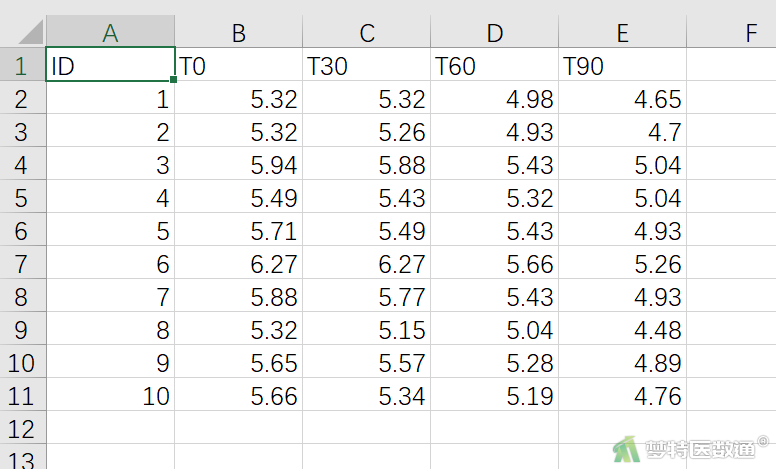
二、问题分析
本案例的分析目的是比较4个时间点的生化指标浓度是否有差异。由于4个时间点的数据属于重复测量数据，可以使用重复测量设计的单因素方差分析(One-Way Repeated Measures ANOVA)。但需要满足5个条件：
条件1：观察变量唯一，且为连续性变量。本研究中观察变量为某生化指标的含量，且数据为连续性变量，该条件满足。
条件2：观察变量为重复测量数据，即不满足独立性。本研究中4个时间点测量的生化指标浓度均是针对同一批样本，因此不满足独立性，该条件满足。
条件3：观察变量不存在显著的异常值。该条件可借助其他软件分析后辅助判断。
条件4：各水平(时间点)观察变量为正态(或近似正态)分布。该条件需要通过软件分析后判断。
条件5：各重复测量水平观察变量的协方差相等，即满足球形假设。该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 数据读取
1. 数据录入
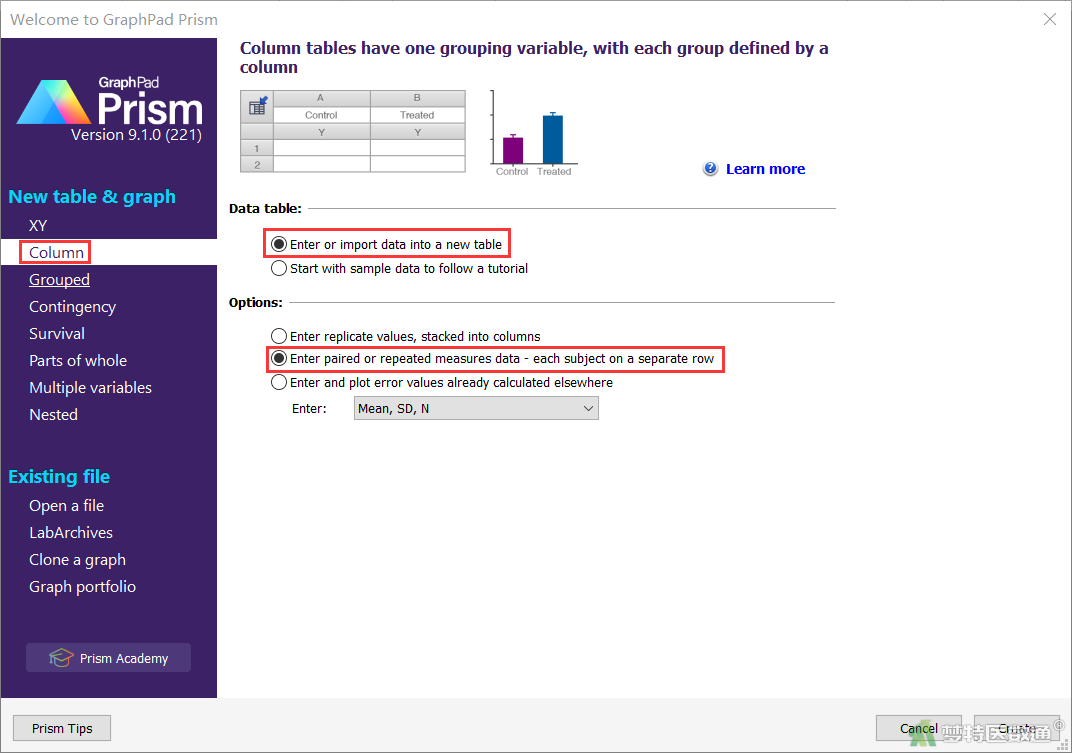
打开GraphPad Prism，在弹出的欢迎界面左侧New table & graph (新建表格或图片)中选择Column (纵列表)，在Data table (数据表)选择Enter or import data into a new table (在新的数据表中写入数据)，在Options (选项)中，选择Enter paired or repeated measures data-each subject on a separate row (输入配对或重复测量数据，每行代表一个实验对象)，单击create创建数据表(图2)。
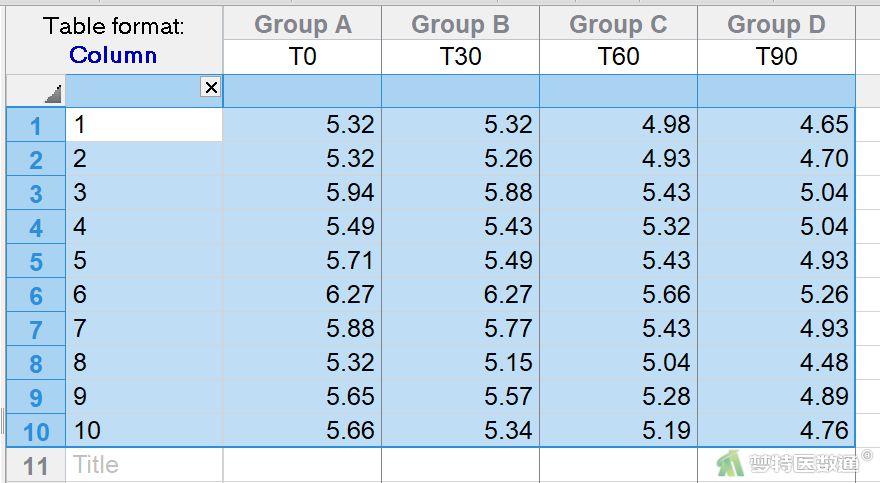
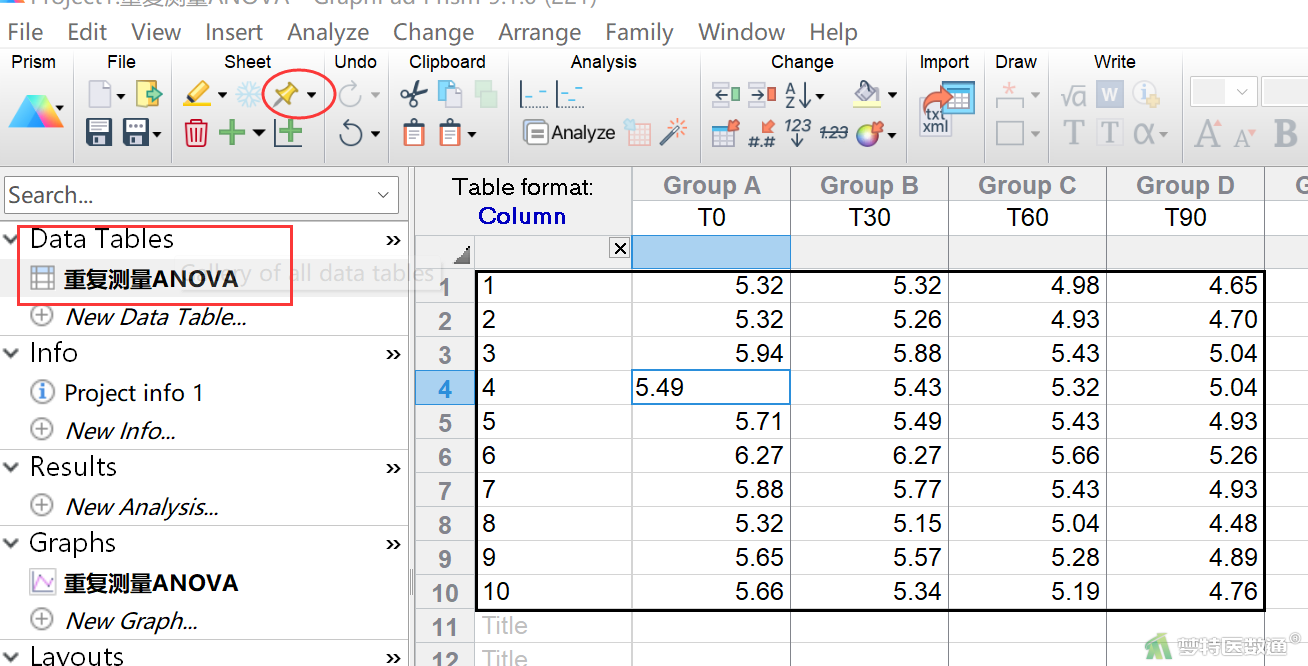
在Group A、B、C和D列输入需要的数据，代表4个不同的时间点的测量值(图3)。
2. 数据导入
用户也可以导入已有的数据，具体过程如下：
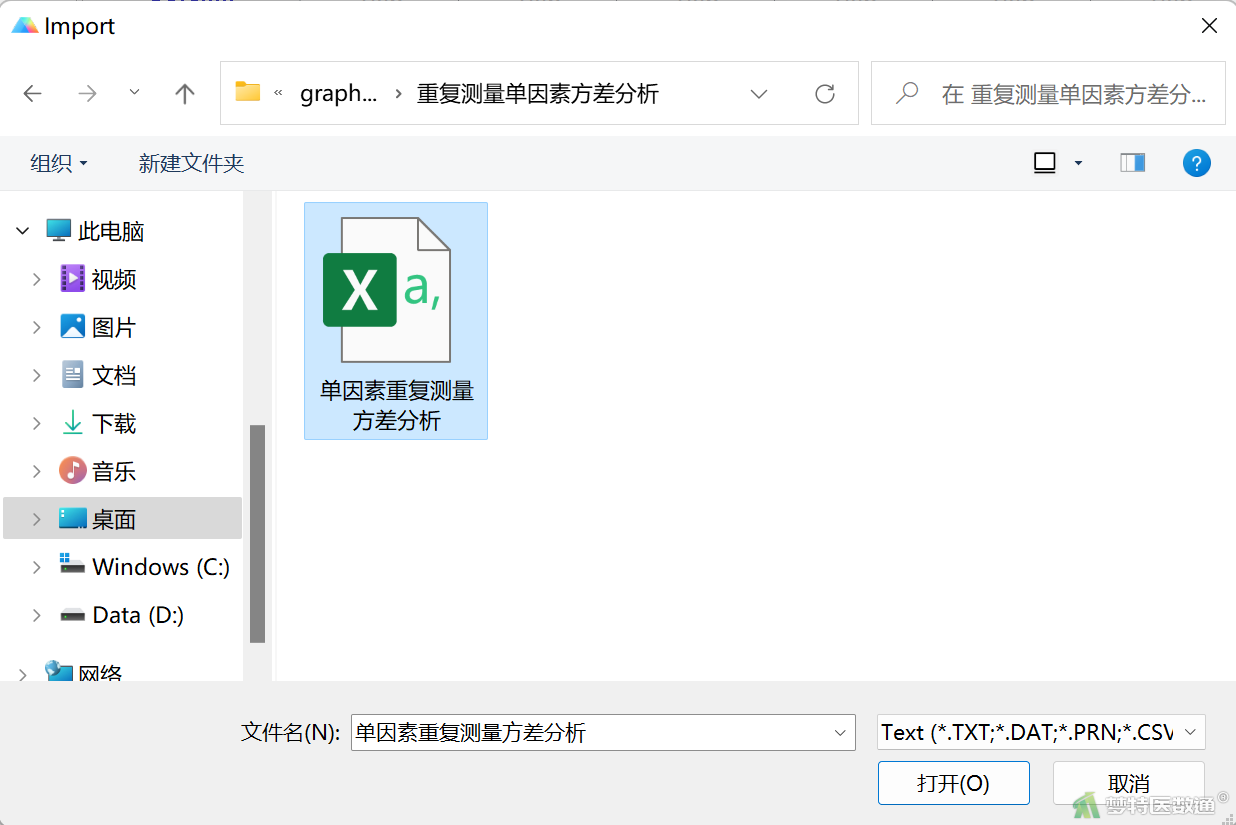
(1) 点击上方工具栏file中的import选项(图4)
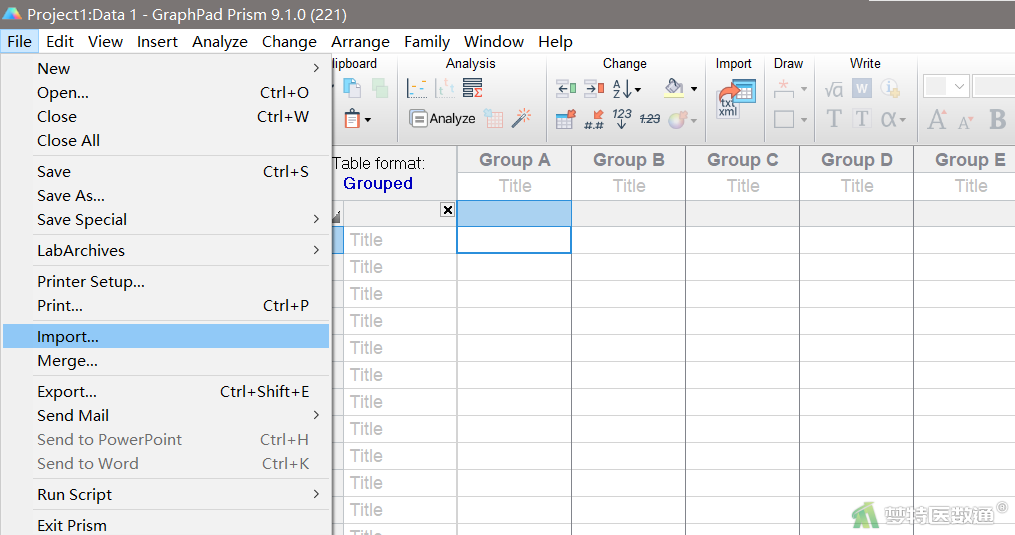
(2) 在弹出的对话框的右下角先选择需要导入的数据存放格式(图5)，然后选择用户的目标文件，单击OK
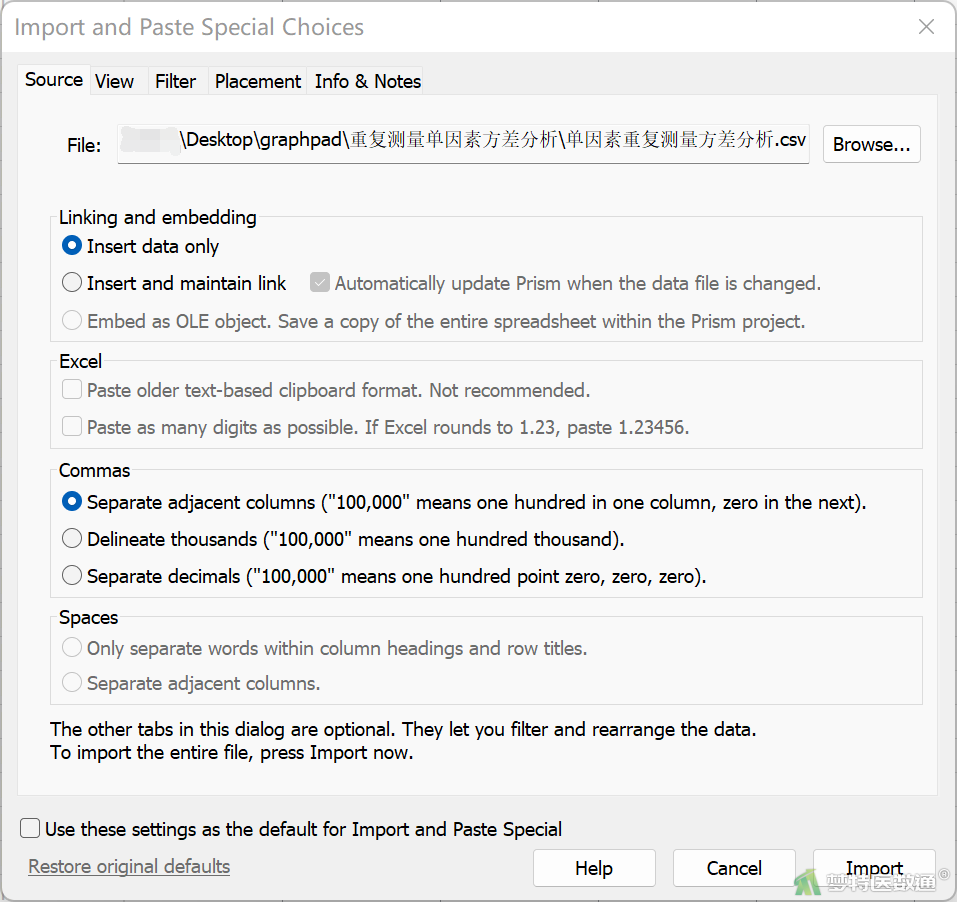
(3) 在随后弹出的对话框Import and Paste Special Choice (导入并粘贴特殊选项，图6)的Linking and embedding (联系和嵌入)中选择Insert data only (仅插入数据)
(4) 点击Import即可导入数据
将数据表重命名为“重复测量ANOVA”，对数据命名有助于日后的文件管理。如有需要，用户可以在Info部分对实验时间、实验编号和项目名称等进行简单描述，或者单击工具栏Sheet选项中的
图标，可以在各表单上添加悬浮笔记，记录需要的信息(图7)。
(二) 适用条件判断
1. 条件3判断 (异常值判断)
观察是否存在异常值，可以通过绘制箱线图来判断。
(1) 软件操作
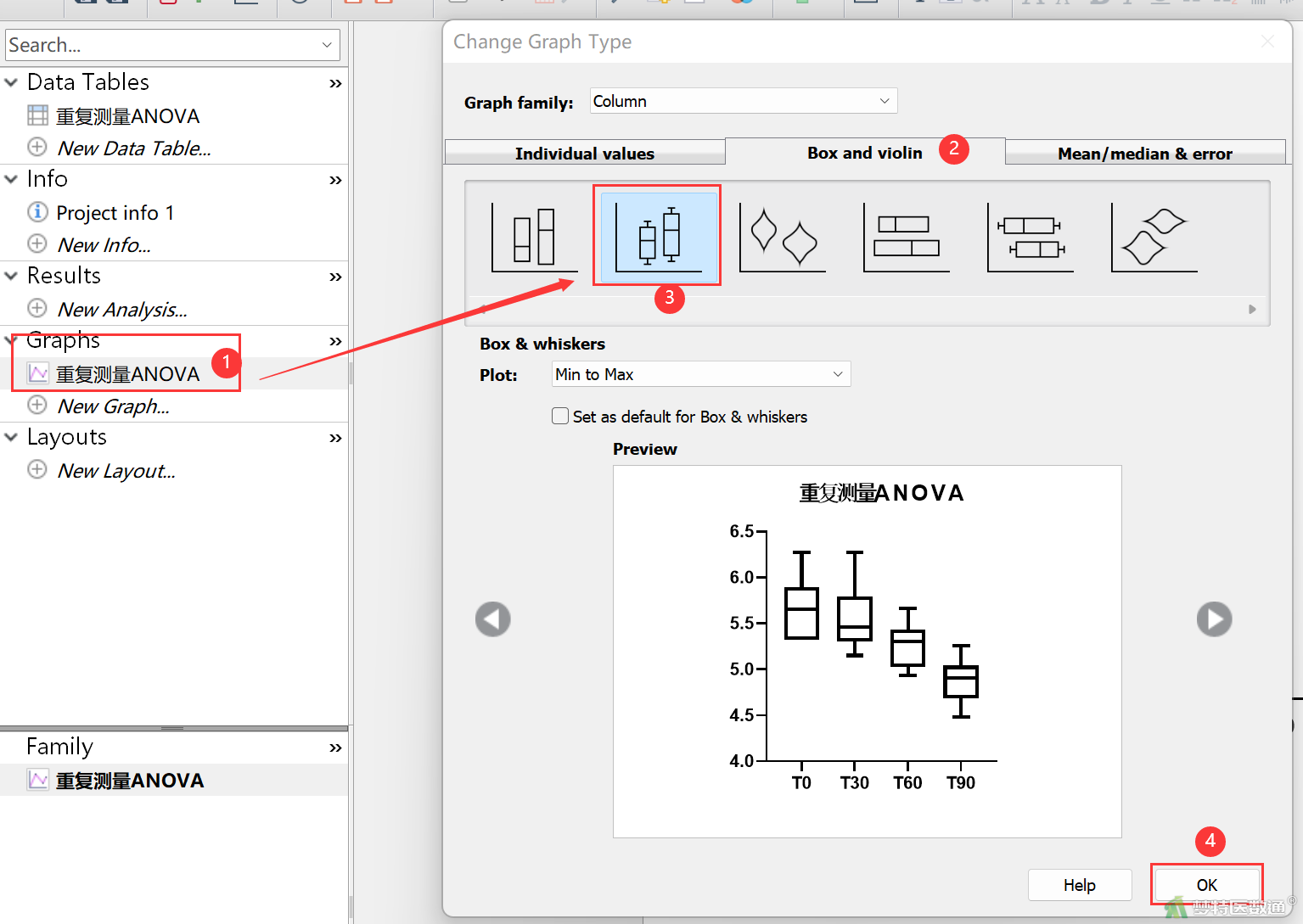
点击左侧导航栏中的Graphs (图片)下属的同名图片文件 (重复测量ANOVA)，弹出Change Graph Type (更改图标类型)界面，选择Box and violin (箱式图和小提琴图)，然后再选择第2个 (带极值的箱式图)，单击OK (图8)，结果如图9所示。
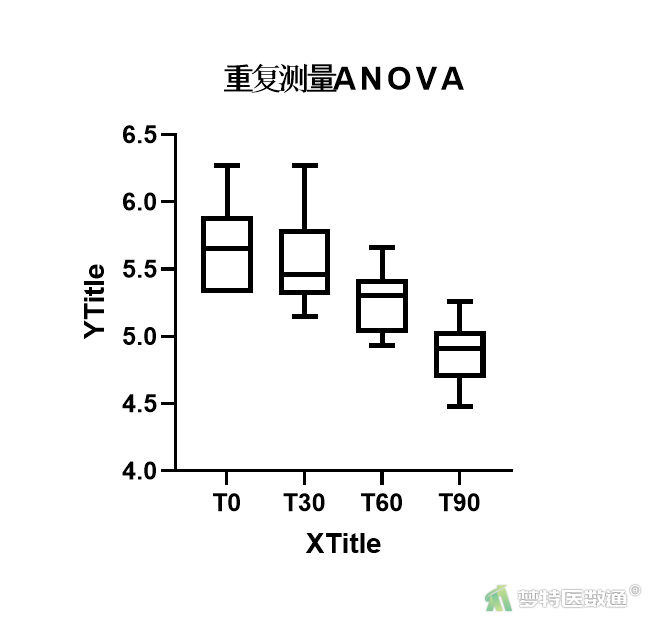
(2) 结果解读
受试者在4组不同时间点某项生化指标含量的箱线图(图9)显示，最大值或最小值均未超过箱体的1.5倍，说明4组均不存在异常值。该条件满足。
更详细的异常值判断方法见“单因素重复测量方差分析(One-Way Repeated Measures ANOVA)——SPSS软件实现”。
2. 条件4判断 (正态性检验)
(1) 软件操作
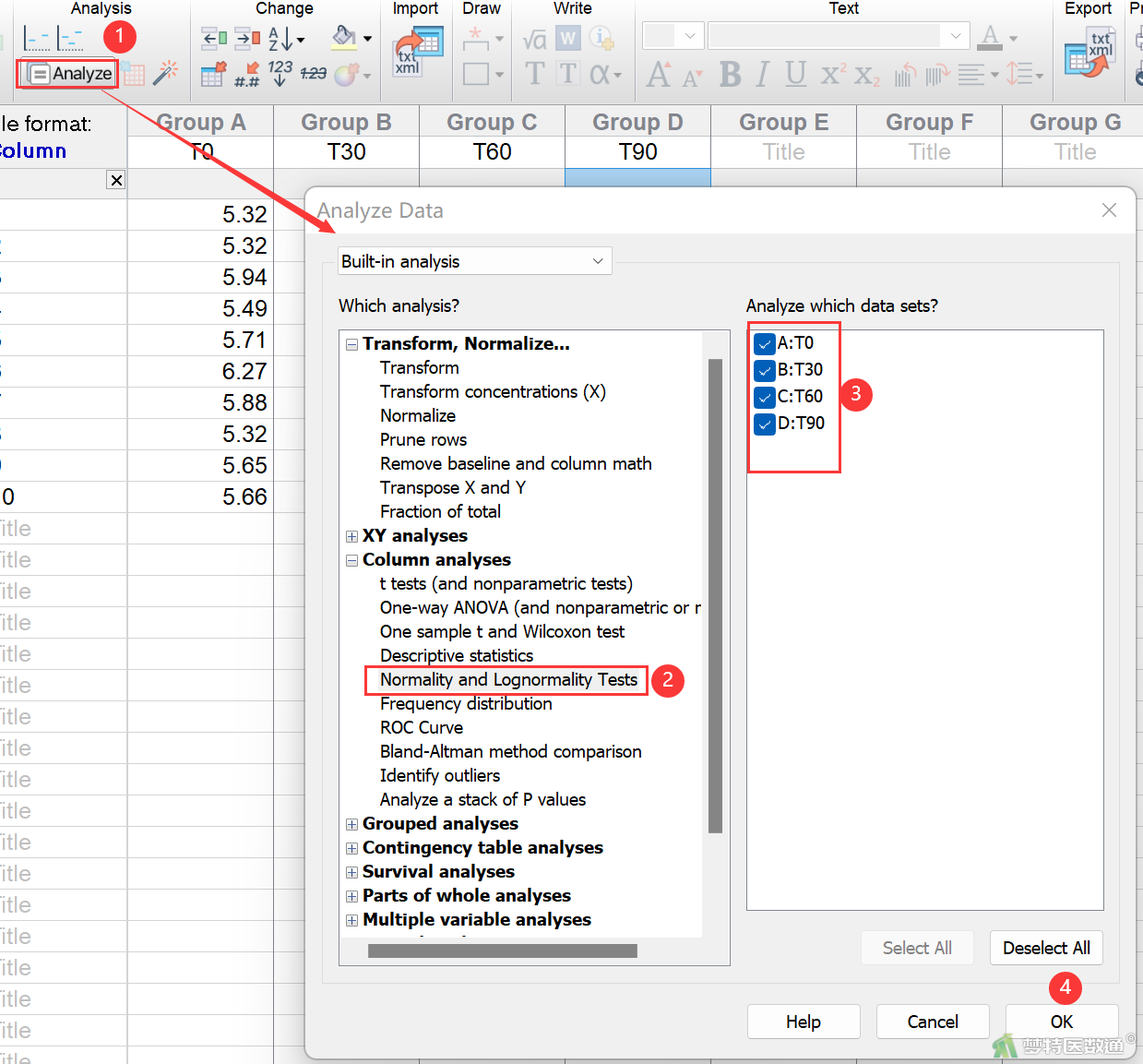
单击工具栏Analysis (分析)选项组中的Analyze (分析)图标按钮
，进入Analyze Data (分析数据)界面。选择Column analyses (纵列表分析)中的Normality and Lognormality Tests (正态性或对数正态性检验)选项，默认勾选“A: T0”、“B: T30”、“C: T60”和“D: T90”，4个数据集，单击OK (图10)，参数设置保持默认选项(图11)，单击OK。
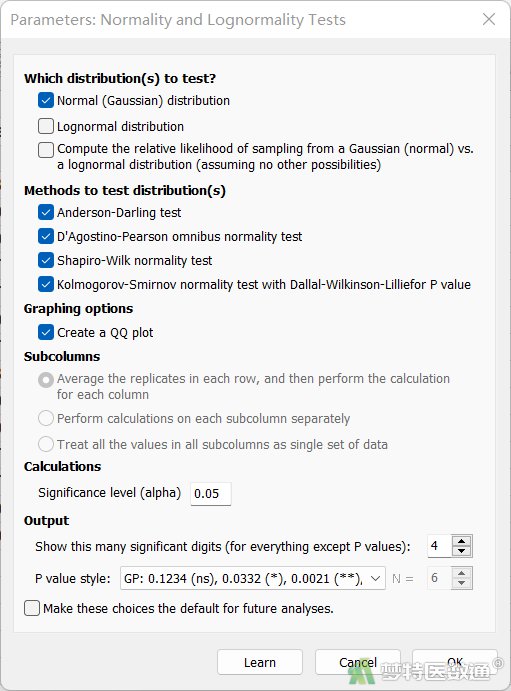
(2) 结果解读
正态性检验结果在Results (结果)中查看。
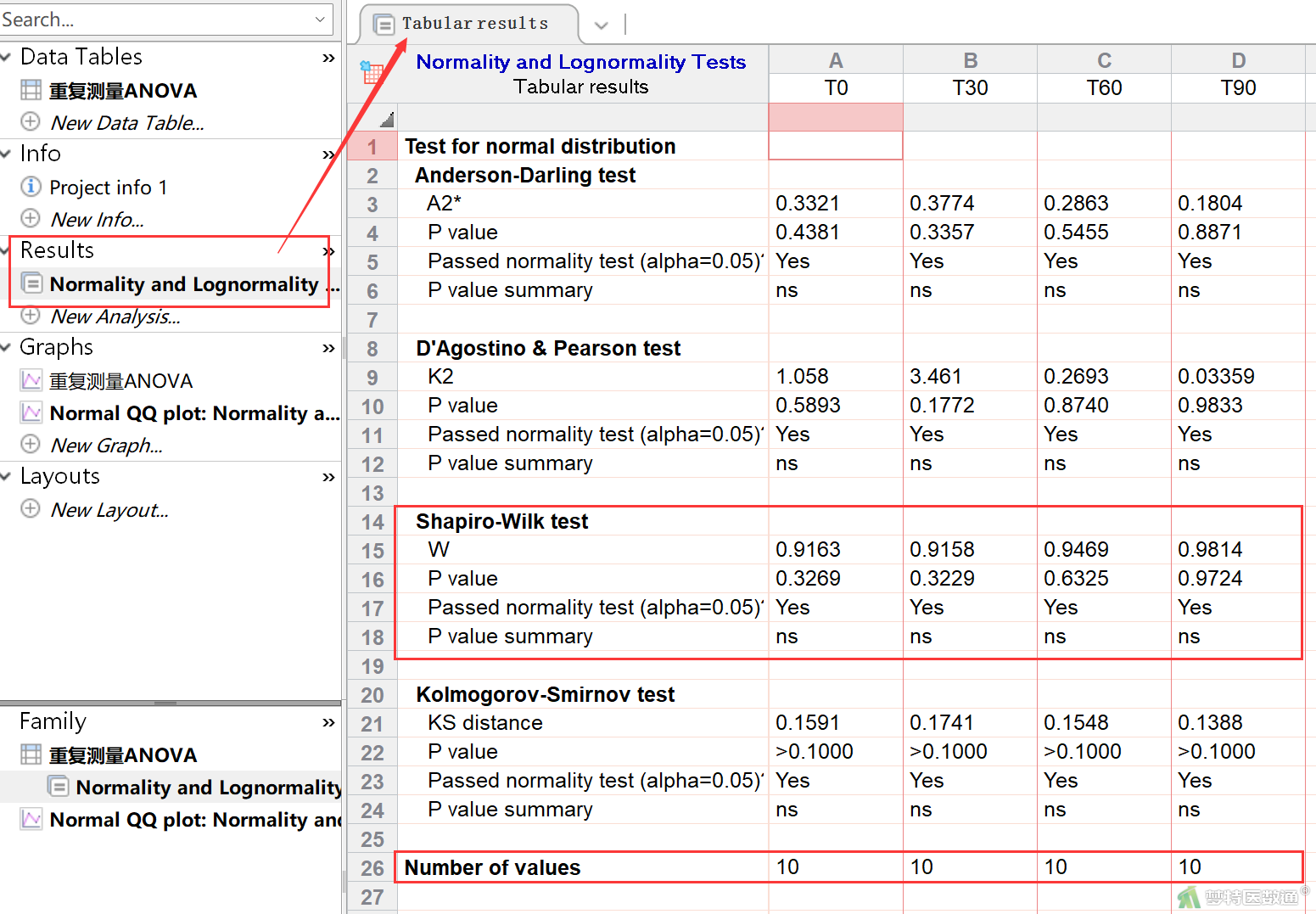
① 4种正态性检验的结果(图12)显示，本例4组数据样本量均为10，为小样本(样本量<50)，因此选择Shapiro-Wilk (夏皮罗-威尔克正态性，S-W)检验的检验效能更高。本案例查看S-W检验结果，可见P值分别为0.3269, 0.3229, 0.6325和0.9724，均大于0.10，提示4组数据均服从正态分布。该条件满足。
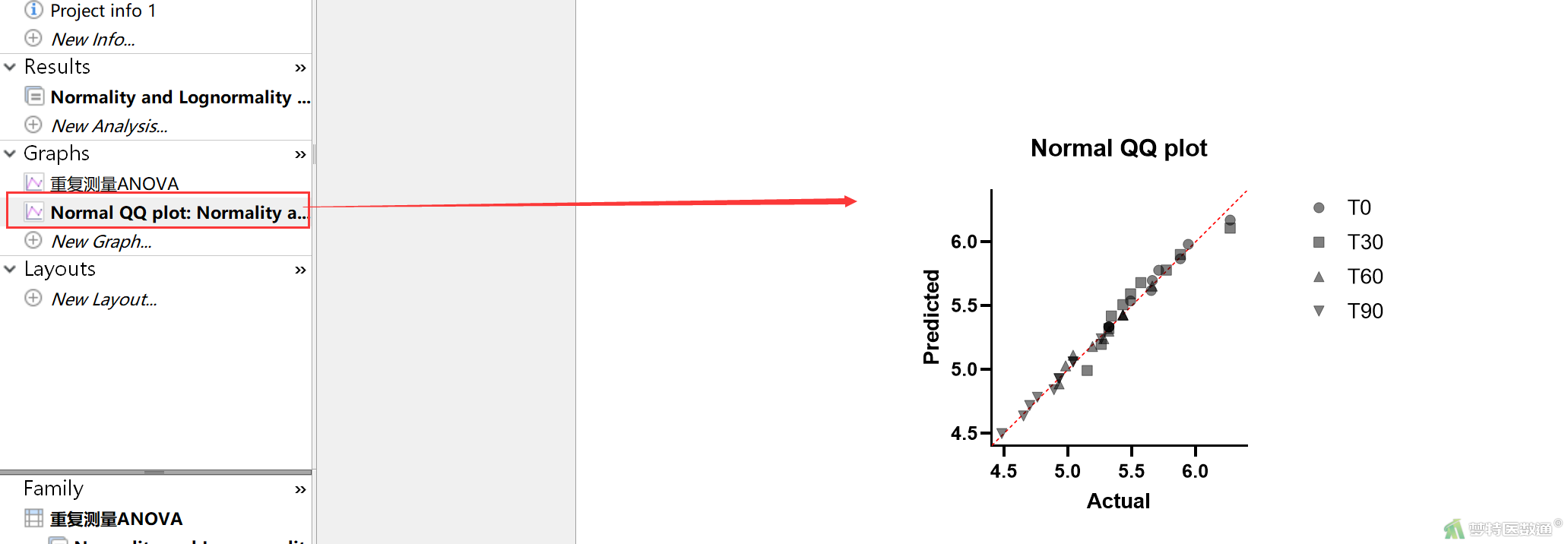
② 单击Graphs (图)中的Normal QQ plot (正态性QQ图)，看以看到4组数据的QQ图 (图13)。QQ图上散点基本围绕对角线分布，也提示数据呈正态分布，说明该数据符合正态性。该条件满足。
3. 条件5判断 (球形假设检验)
(1) 软件操作
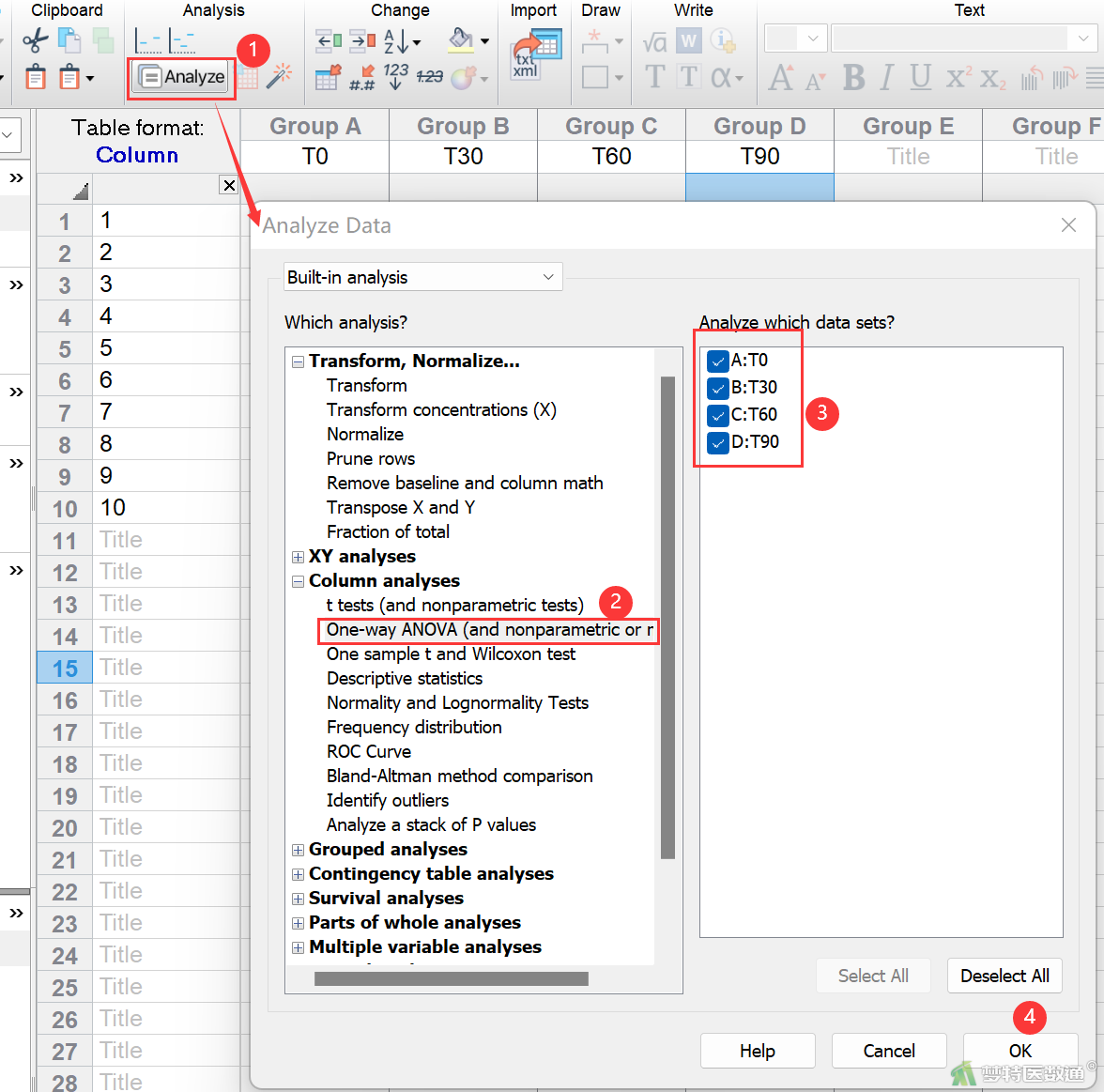
① 单击工具栏Analysis (分析)选项组中的Analyze (分析)图标按钮，进入Analyze Data (分析数据)界面。选择Column analyses (纵列表分析)中的One-way ANOVA (and nonparametric or mixed) (单因素方差分析或非参数检验或混合模型)选项，默认勾选“A: T0”、“B: T30”、“C: T60”和“D: T90” 4个数据集，单击OK (图14)，单击OK。
② 在弹出的窗口中 (图15)，首先在Experimental design (实验设计)中选择Each row represents matched, or repeated measure, data (每行为配对数据或者是重复测量数据)。其次由于已经满足正态性检验，所以可以用参数检验，选择Yes, Use ANOVA (使用方差分析)。最下面的Assume sphericity (球形假设)检验方法默认选择非球性选项No, Use the Geisser-Greenhouse correction. Recommended. (即先假定各组数据为非球性，采用Geisser-Greenhouse矫正方法计算，具体是否满足还需要进一步查看分析结果)。
(2) 结果解读
方差齐性检验结果在Results (结果)中查看。
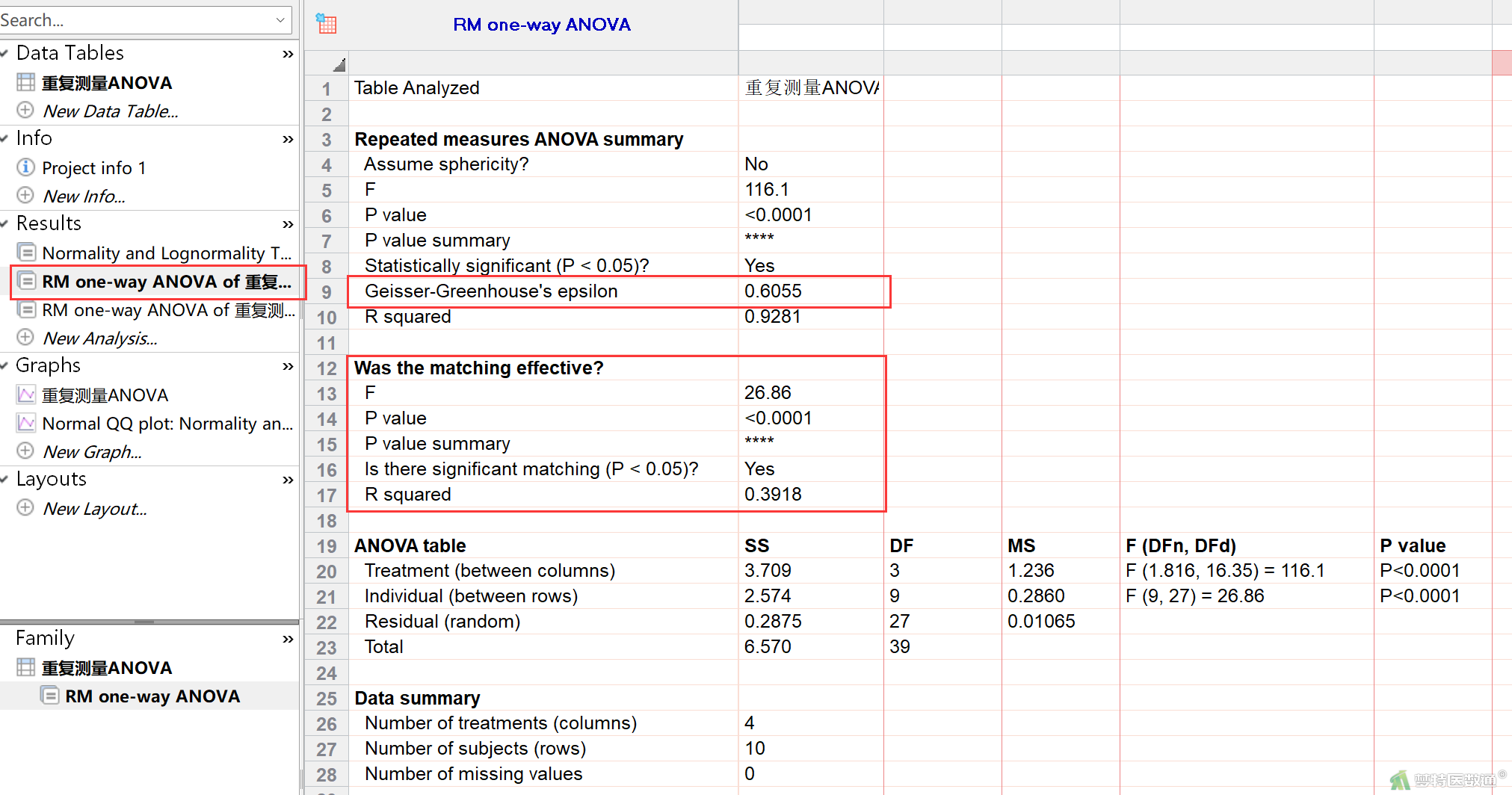
配伍显著性检验结果(matching effective部分，图16)显示，P<0.0001，表明配伍显著。其次，重复测量方差分析结果(Repeated measures ANOVA summary部分，图16)显示，epsilon为0.6055(校正系数Geisser-Greenhouse’s epsilon反映了对球性假设的偏离程度，当epsilon等于或近似于1时表明对球性无偏离，即满足球对称假设；当epsilon小于1或距离1越远时，表明偏离越大)，不符合球形假设。此时可以采用Geisser-Greenhouse矫正的分析方法。具体球形假设的统计操作可见“单因素重复测量方差分析(One-Way Repeated Measures ANOVA)——SAS软件实现”。
(三) 统计描述及推断
1. 软件操作
① 由上述条件判断可知，数据满足正态性，且不满足球形假设，因此可以采用Geisser-Greenhouse矫正的重复测量的单因素方差分析。
② 操作与判断球形假设检验相同。在图15的窗口最下面选择No, Use the Geisser-Greenhouse correction. Recommended. (使用Geisser-Greenhouse矫正的重复测量单因素方差分析)。当epsilon <0.75时，使用Geisser-Greenhouse方法校正；当epsilon >0.75时，使用Huynh-Feldt方法校正。
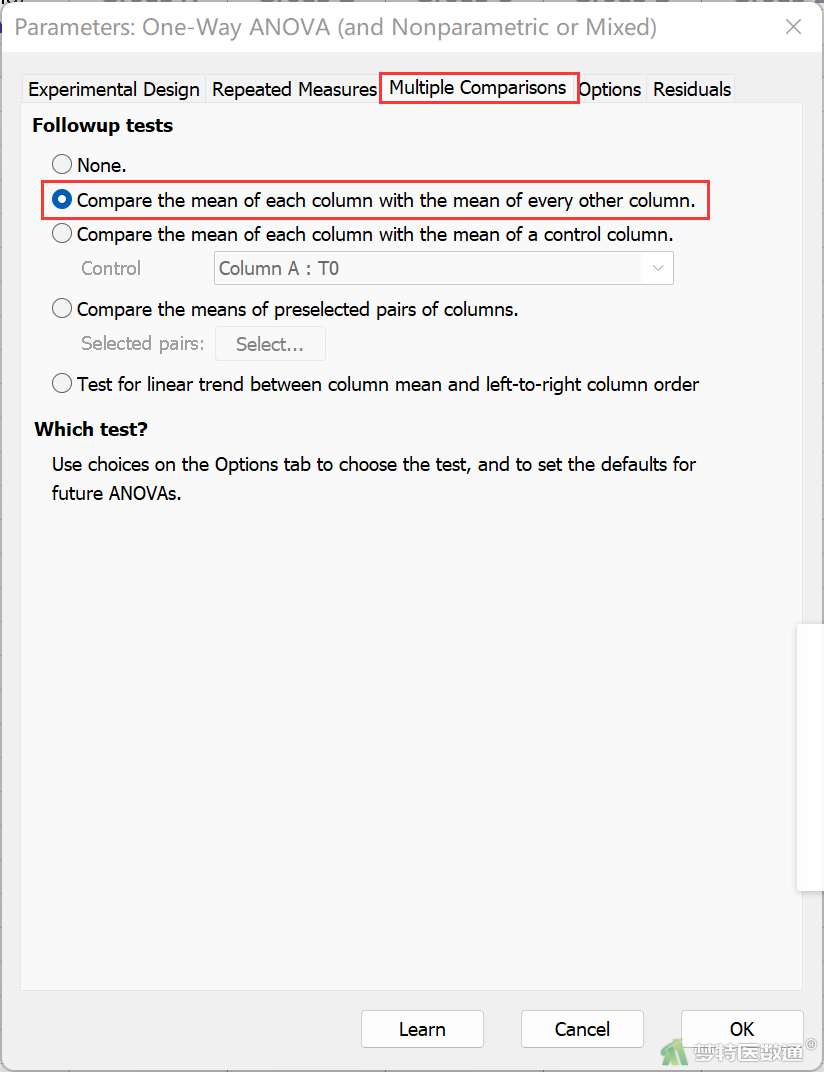
③ 如所示，在Multiple Comparisons (多重比较)窗口选中Compare the mean of each column with the mean of every other column (任意两组进行两两比较) (图17)。
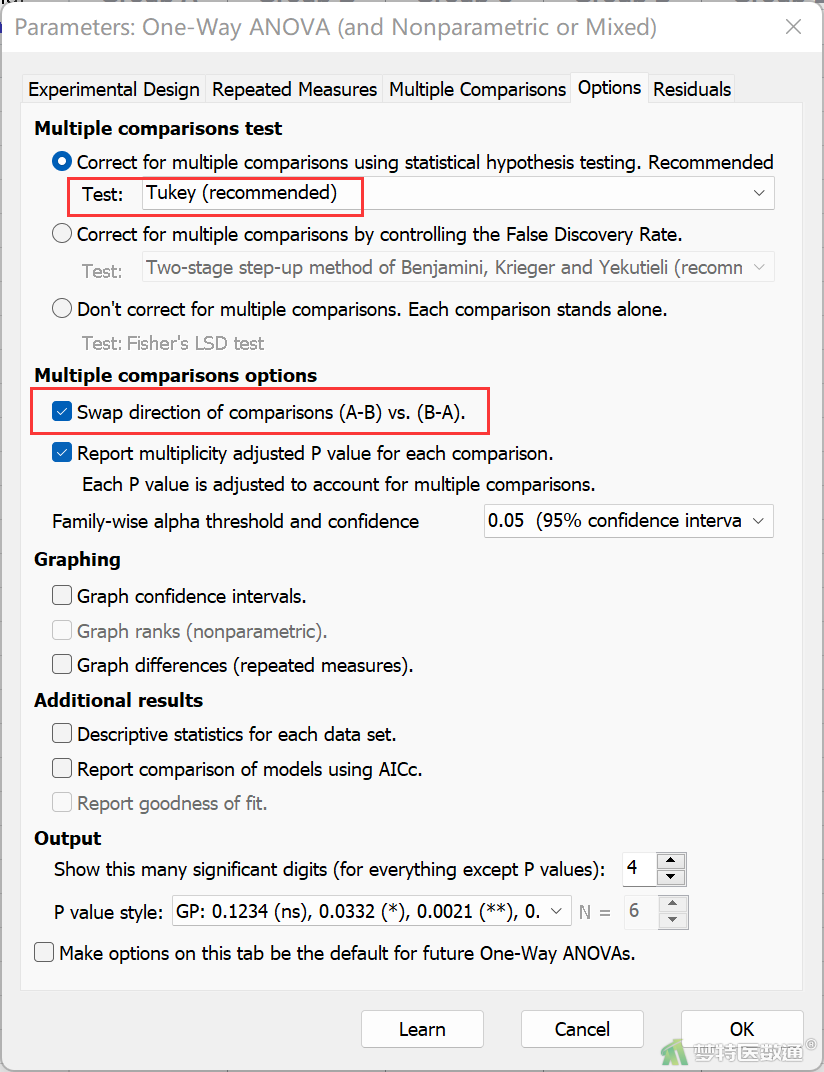
④ 再对应的Options (选项)窗口默认选则Tukey检验进行两两比较，并勾选Swap direction of comparisons (A-B)vs. (B-A). (调换比较方向，图18)。
2. 结果解读
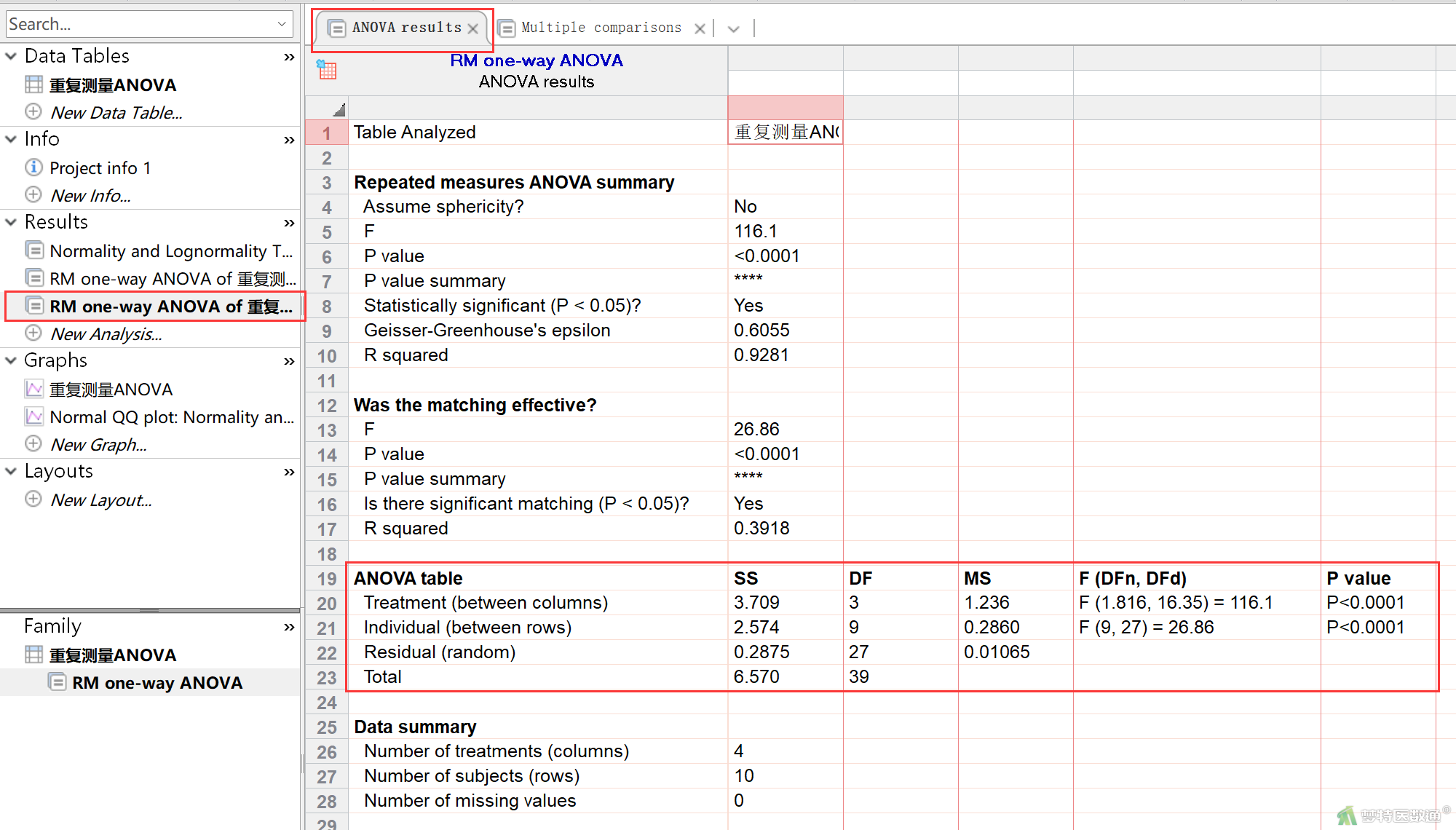
矫正单因素方差分析结果在Results (结果)中查看。
①如图19所示，对不同时间点的指标浓度差异性检验结果显示，Treatment (处理因素检验)统计量F=116.1，P<0.0001，认为不同时间点的指标浓度值存在统计学差异；对不同个体的指标浓度差异性检验结果显示，Individual (即组间个体因素检验)统计量F=26.86，P<0.0001，认为不同受试者的指标浓度值也存在统计学差异。
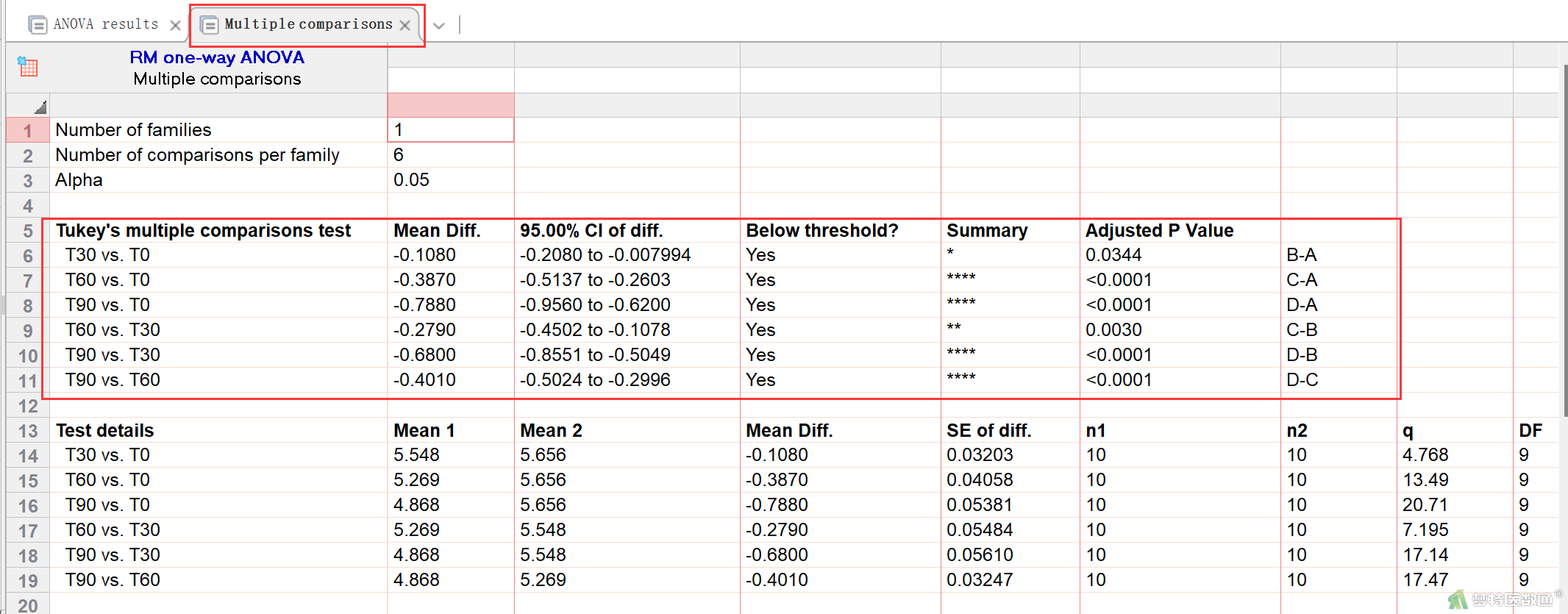
② 上面分析得出了“不同时间点生化指标浓度差异有统计学意义”的结论，但是具体哪些组别之间存在差异尚不清楚，因此需要进行事后检验，开展两两比较。两两比较的结果(图20)为：T0和T30之间的差异为0.1080，差异有统计学意义(P=0.0344)；T0和T60之间的差异为0.3870，差异有统计学意义(P<0.0001)；T0和T90之间的差异为0.7880，差异有统计学意义(P<0.0001)；T30和T60之间的差异为0.2790，差异有统计学意义(P=0.0030)；T30和T90之间的差异为0.6800，差异有统计学意义(P<0.0001)；T60和T90之间的差异为0.4010，差异有统计学意义(P<0.0001)。
③ 综上，事后检验结果表明，放置0分钟、30分钟、60分钟、90分钟的指标浓度两两比较差异均有统计学意义。结合放置0分钟、30分钟、60分钟、90分钟后的指标浓度值，可以得出结论：随着放置时间的延长，指标浓度逐渐降低。
图形的生成与美化同“GraphPad Prism纵列表统计分析——重复测量单因素方差分析 (One-Way Repeated Measures ANOVA) (链接)”
其他更多设置，可以根据需要在相应部分进行操作。