在前面文章中介绍了两因素方差分析(Two-way ANOVA)——不存在交互作用时在Stata软件中的实现,本篇文章将实例演示在Stata软件中实现两因素方差分析——存在交互作用时的操作步骤。
关键词:Stata; 两因素方差分析; 交互作用; 主效应; 单独效应; 简单效应
一、案例介绍
观察A、B两种镇痛药物联合运用在产妇分娩时的镇痛效果。A药取3个剂量:1.0、2.5、5.0mg,对应变量drug_a的1、2、3组;B药也取3个剂量:5.0、15.0、30.0μg,对应变量drug_b的1、2、3组,共9个处理组。将27名产妇随机分成9组,每组3名产妇,记录每名产妇分娩时的镇痛时间Time (min)。试分析A、B两药联合运用的镇痛效果。部分数据见图1。本文案例可从“附件下载”处下载。
二、问题分析
本案例的分析目的是分析A、B两种药物联合运用的镇痛效果。临床上,药物之间联合运用往往会相互影响,这种影响可能为正向的增强效应,也可能为反向的拮抗作用。针对这种情况,可以使用多因素方差分析,由于本案例为药物A和药物B两个因素,因此可以使用两因素方差分析。但需要满足6个条件:
条件1:观察变量唯一,且为连续变量。本研究中观察变量只有镇痛时间,且为连续变量,该条件满足。
条件2:有两个因素,且都为分类变量。本研究中有A、药物B物两个因素,都为分类变量,该条件满足。
条件3:观测值之间相互独立。本研究中各研究对象的观测值都是独立的,不存在互相干扰的情况,该条件满足。
条件4:观察变量不存在显著的异常值,该条件需要通过软件分析后判断。
条件5:各组、各水平观测值为正态(或近似正态)分布,该条件需要通过软件分析后判断。
条件6:相互比较的各处理水平(组别)的总体方差相等,即方差齐同,该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 适用条件判断
两因素方差分析过程中使用残差判断异常值,先使用两因素方差分析生成因变量残差。
1. 生成因变量残差
(1) 软件操作
anova time drug_a drug_b drug_a#drug_b predict e, residual
(2) 结果解读
通过“Data Editor”视图可以看到生成了一列新的变量“e (残差)”(图2)。
2. 条件4判断(异常值判断)
(1) 软件操作
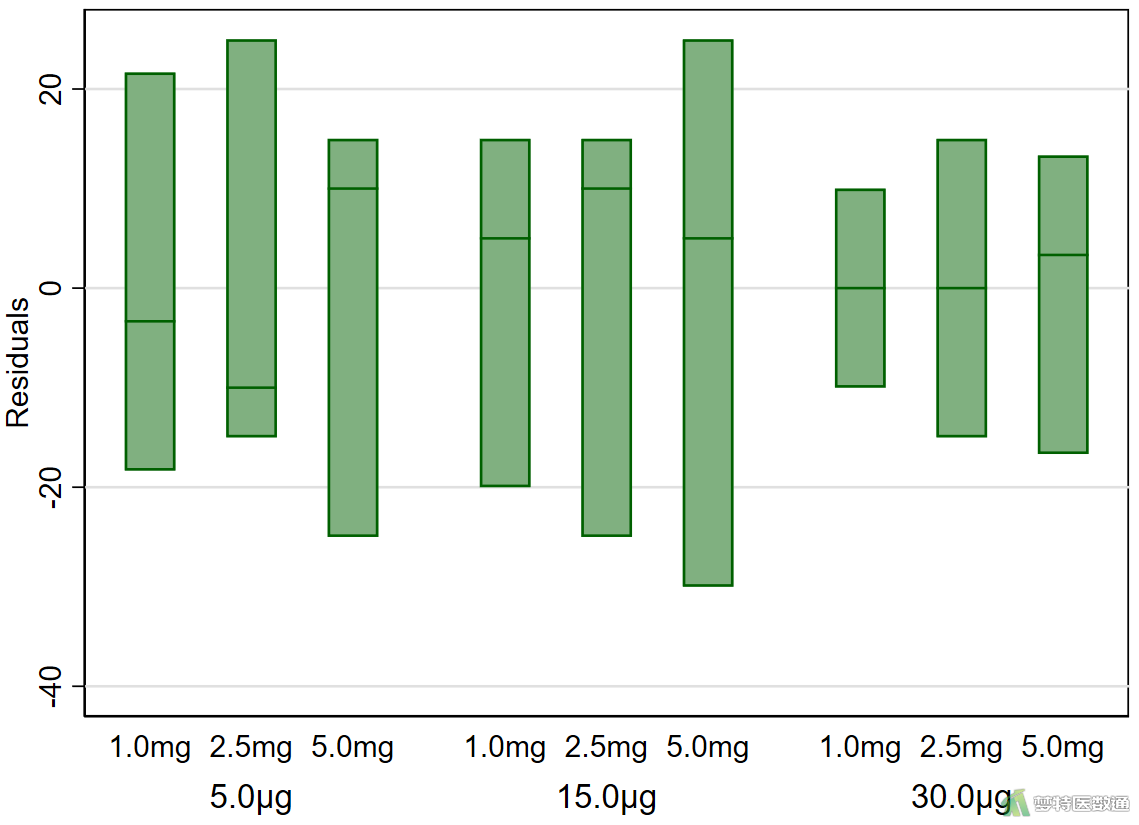
绘制残差箱线图(图3)。
graph box e, over(drug_a, relabel(1 "1.0mg" 2 "2.5mg" 3 "5.0mg")) over(drug_b, relabel(1 "5.0μg" 2 "15.0μg" 3 "30.0μg"))
(2) 结果解读
图3残差的箱线图未提示任何异常值和极端值,满足条件4。
3. 条件5判断(正态性检验)
(1) 软件操作
两因素方差分析时,需要分别考察每一组的正态性或使用残差考察整体数据的正态性。
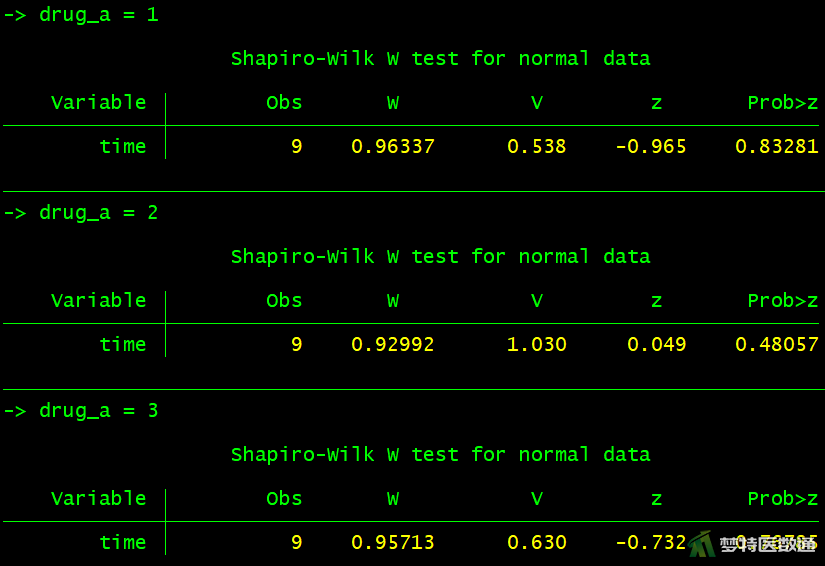
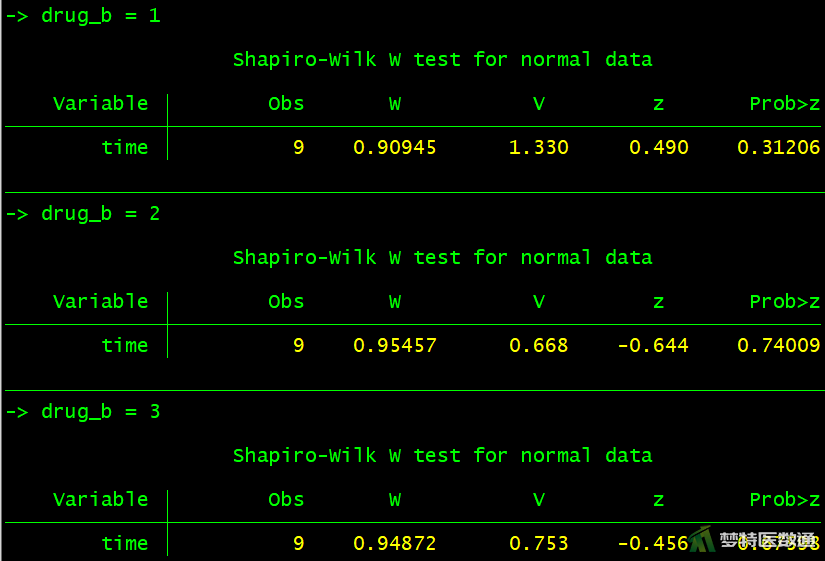
①分别考察每一组数据的正态性,结果如图4-1、图4-2所示。
bysort drug_a: swilk time bysort drug_b: swilk time
②使用残差考察整体数据的正态性,结果如图5所示。
swilk e

(2) 结果解读
图4-1、图4-2的正态性检验结果显示各组的P值均>0.1,提示各组数据均服从正态分布。图5的残差正态性检验结果显示,P值>0.1,提示整体数据服从正态分布。综上,本案例满足条件5。此外,也可以使用Q-Q图判断正态性(读者可自行操作)。
4. 条件6判断(方差齐性检验)
(1) 软件操作
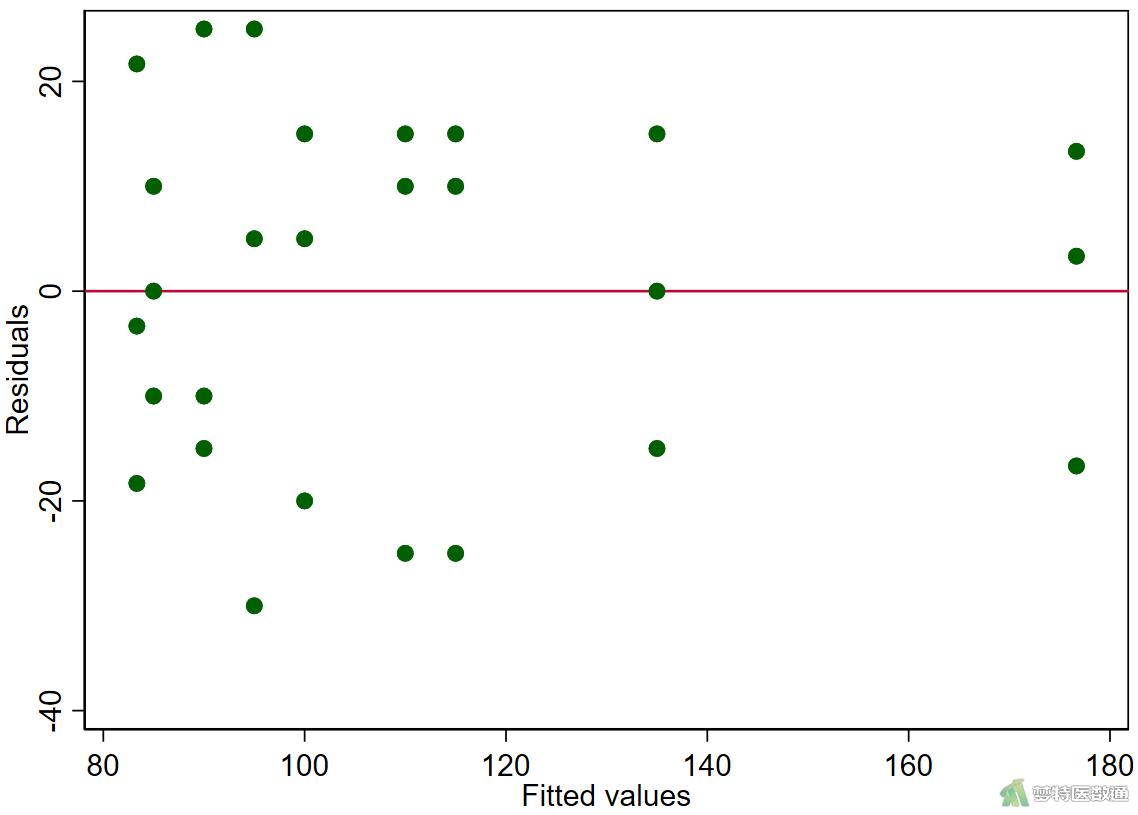
①绘制残差图检验方差齐性,结果如图6所示。
rvfplot, yline(0)
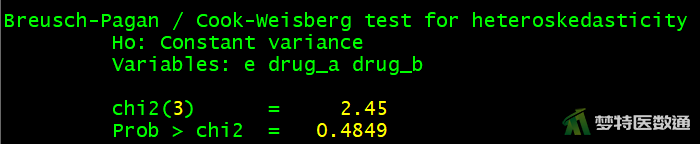
②使用BP(Breusch-Pagan)法检验方差齐性,结果如图7所示。
estat hettest e drug_a drug_b
(2) 结果解读
由图6可以看出,残差均匀地分布在其均值的上下两侧,提示观察变量的残差满足方差齐性;根据图7显示的结果,P>0.1,不能拒绝方差相等的原假设,提示观察变量的残差满足方差齐性。综上,本案例满足条件6。
(二) 统计描述
1. 软件操作
tabulate drug_a drug_b, summarize(time)
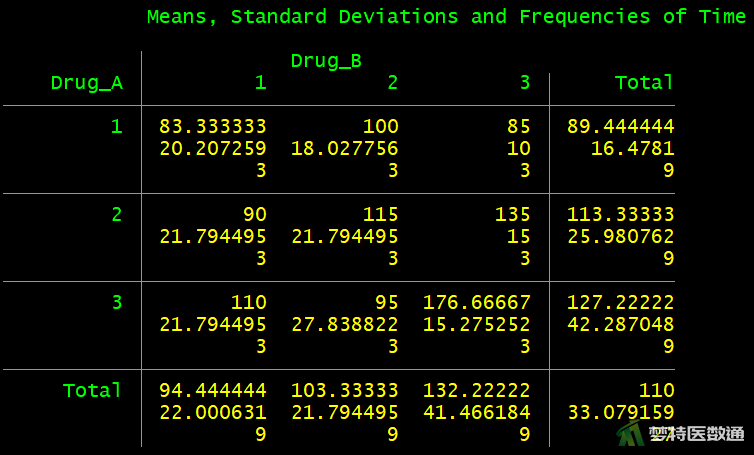
2. 结果解读
图8的结果中列出了各组的均值和标准差,可知药物A在1.0 mg水平(drug_a=1),药物B为5.0、15.0、30.0 μg水平(drug_b=1、2、3)时,镇痛时间分别为:83.333±20.207、100.000±18.028、85.000±10.000 min;药物A在2.5 mg水平(drug_a=2),药物B为5.0、15.0、30.0 μg水平(drug_b=1、2、3)时,镇痛时间分别为:90.000±21.794、115.000±21.794、135.000±15.000 min;药物A在5.0 mg水平(drug_a=3),药物B为5.0、15.0、30.0 μg水平(drug_b=1、2、3)时,镇痛时间分别为:110.000±21.794、95.000±27.839、176.667±15.275 min。
(三) 两因素方差分析
1. 软件操作
margins drug_a, over(drug_b) plot
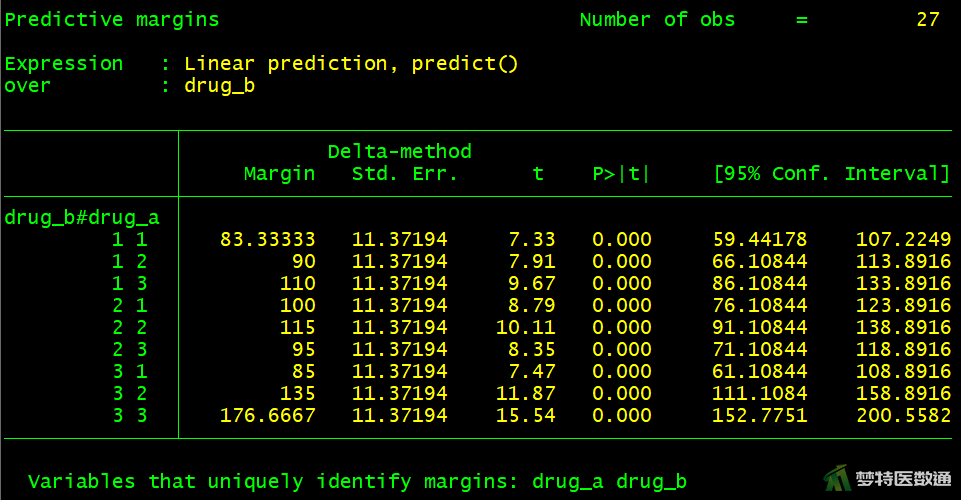
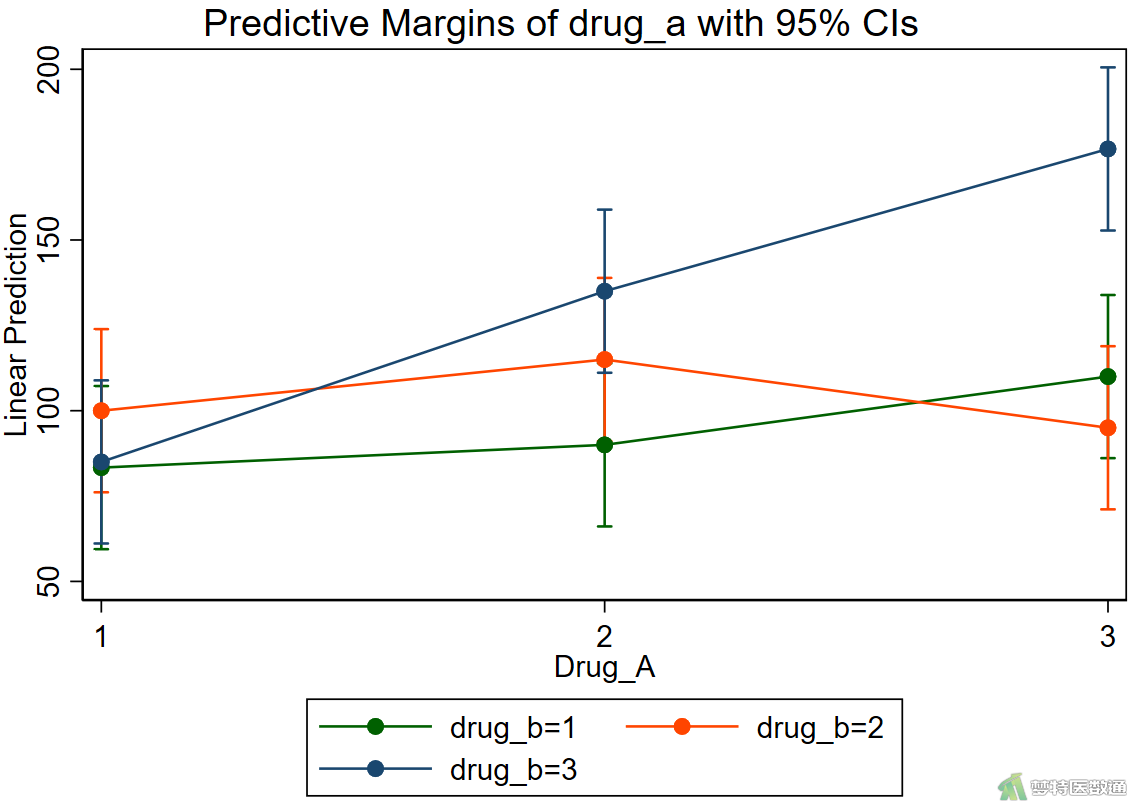
2. 结果解读
图9的结果显示了药物A和药物B估算边际均值的相关统计量结果;图10绘制了各组镇痛时间的变化情况,提示两种药物的变化曲线趋势并不平行,存在明显的交互作用。
(四) 交互作用判断
由于本案例有两个因素(一个为药物A,另一个为药物B),因此需要首先判断两个因素(两种药物)之间是否存在交互作用。尽管通过图10的变化趋势已经提示两药物之间存在明显的交互作用,但仍需要统计学推断结果的支持。如果交互作用有统计学意义,则需要分析简单效应。
1. 软件操作
anova time drug_a drug_b drug_a#drug_b
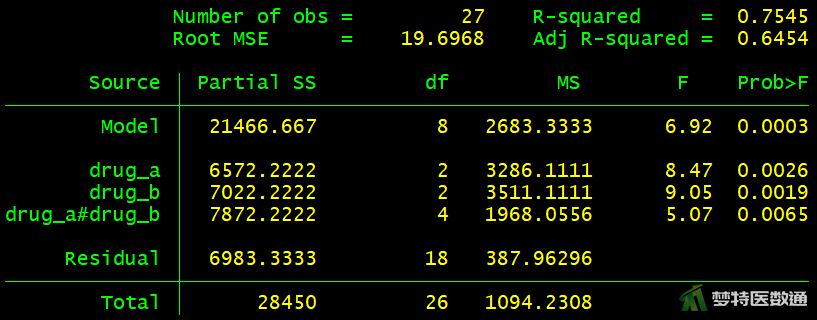
2. 结果解读
图11结果显示,药物A与药物B之间的交互作用结果为Fdrug_a#drug_b=5.07,P=0.0065,表明A药与B药之间的交互作用有统计学意义。因此,本案例需要分析简单效应。
(五) 简单效应分析
1. 软件操作
(1) “anovalator包”安装
简单效应的分析可使用“anovalator”命令,首先要在Stata中安装“anovalator包”。有两种安装方法:
①直接输入命令“ssc install anovalator”安装。
②输入命令“search anovalator”,结果见图12-1。
点击图12-1 中方框标记部分, 结果见图12-2。
点击图12-2 中“click here to install”,完成安装。
(2) 简单效应分析
anovalator drug_a drug_b, simple fratio
anovalator drug_b drug_a, simple fratio

2. 结果解读
(1) 药物A的简单效应
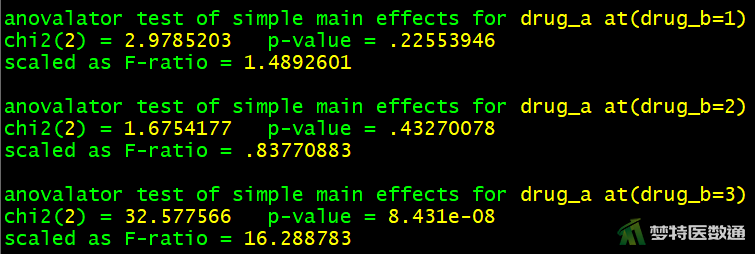
图13-1显示了药物A的简单效应分析结果,可知,在药物B为5.0 μg水平(drug_b=1)时,药物A各水平之间的镇痛时间差异无统计学意义(F=1.490,P=0.226);在药物B为15.0 μg水平(drug_b=2)时,药物A各水平之间的镇痛时间差异无统计学意义(F=0.838,P=0.433);在药物B为30.0 μg水平(drug_b=3)时,药物A各水平之间的镇痛时间差异有统计学意义(F=16.289,P<0.001)。
(2)药物B的简单效应
图13-2显示了药物B的简单效应分析结果,可知,在在药物A为1.0 mg水平(drug_a=1)时,药物B各水平之间的镇痛时间差异无统计学意义(F=0.652,P=0.521) 在药物A为2.5 mg水平(drug_a=2)时,药物B各水平之间的镇痛时间差异有统计学意义(F=3.931,P=0.020);在药物A为5.0 mg水平(drug_a=3)时,药物B各水平之间的镇痛时间差异有统计学意义(F=14.613,P<0.001)。
(六) 事后检验(两两比较)
1. A药的简单效应事后检验
上面分析得出了“在药物B为30.0 μg水平(drug_b=3)时,药物A各水平之间的镇痛时间差异有统计学意义”的结论。由于药物A在药物B为5.0 μg和15.0 μg水平下的整体检验差异无统计学意义,此时便不再进行事后两两比较。现对药物A在药物B为30.0 μg水平时进行事后检验,结果如图14所示。
(1) 软件操作
margins drug_a, at(drug_b=3) pwcompare(effects)

(2) 结果解读
根据图14中结果可知,药物A浓度为2.5 mg(drug_a=2)和5.0 mg(drug_a=3)与1.0 mg(drug_a=1)相比,均值差逐渐增大。2.5 mg比1.0 mg时均值增加了50.00 min,至5.0 mg时增加了91.67 min,差异均有统计学意义(P<0.001);2.5 mg到5.0 mg时增加了41.67 min,差异有统计学意义(P=0.018)。表明,在药物B为30.0 μg(drug_b=3)水平时,随着药物A浓度的增加,镇痛时间呈上升趋势。
2. B药的简单效应事后检验
上面分析得出了“在药物A为2.5 mg(drug_a=2)和5.0 mg(drug_a=3)水平时,药物B各水平之间的镇痛时间差异均有统计学意义”的结论。由于药物B在药物A的1.0 mg水平下的整体检验差异无统计学意义,此时便不再进行事后两两比较。现对药物B在药物A为2.5 mg和5.0 mg水平时进行事后检验,结果如图15-1、图15-2所示。
(1) 软件操作
margins drug_b, at(drug_a=2) pwcompare(effects)

margins drug_b, at(drug_a=3) pwcompare(effects)

(2) 结果解读
根据图15-1、图15-2中结果可知,当药物A为2.5 mg(drug_a=2)时,药物B浓度30.0 μg(drug_b=3)与5.0 μg(drug_b=1)相比,镇痛时间差异有统计学意义(P=0.012),30.0 μg(drug_b=3)与15.0 μg(drug_b=2)相比以及15.0 μg(drug_b=2)与5.0 μg(drug_b=1)相比差异均无统计学意义(P>0.05)。当药物A为5.0 mg(drug_a=3)时,药物B浓度30.0 μg(drug_b=3)与15.0 μg(drug_b=2)相比,镇痛时间差异有统计学意义(P<0.001),30.0 μg(drug_b=3)与5.0 μg(drug_b=1)相比,镇痛时间差异有统计学意义(P=0.001),但15.0 μg(drug_b=2)与5.0 μg(drug_b=1)相比,镇痛时间差异无统计学意义(P=0.363)。
四、结论
本研究采用两因素方差分析探讨A、B两种镇痛药物联合运用在产妇分娩时的镇痛效果。通过对模型残差绘制箱线图提示,数据不存在异常值;通过Shapiro-Wilk检验,提示残差近似服从正态分布;通过对残差绘制残差图和进行BP(Breusch-Pagan)检验,提示数据总体方差相等;方差分析结果显示两药物之间存在交互作用(F drug_a#drug_b =5.07,P=0.0065),故进行简单效应分析。
药物A在1.0 mg水平,药物B为5.0、15.0、30.0 μg水平时,镇痛时间分别为:83.333±20.207、100.000±18.028、85.000±10.000 min;药物A在2.5 mg水平,药物B为5、15、30 μg水平时,镇痛时间分别为:90.000±21.794、115.000±21.794、135.000±15.000 min;药物A在5.0 mg水平,药物B为5、15、30 μg水平时,镇痛时间分别为:110.000±21.794、95.000±27.839、176.667±15.275 min。
药物A的简单效应分析显示,在药物B为30.0μg(drug_b=3)水平时,药物A各水平之间的镇痛时间差异有统计学意义(F=16.289,P<0.001)。但在药物B为5.0μg(drug_b=1)和15.0μg(drug_b=2)水平时,药物A各水平之间的镇痛时间差异均无统计学意义(P>0.05)。对药物A在药物B为30.0μg水平时进行两两比较显示,1.0mg至2.5mg时均值增加了50.00min,至5.0mg时增加了91.67min,差异均有统计学意义(P<0.001);表明,在药物B为30.0μg水平时,随着药物A浓度的增加,镇痛时间呈上升趋势。
药物B的简单效应分析显示,在药物A为1.0mg(drug_a=1)水平时,药物B各水平之间的镇痛时间差异无统计学意义(F=0.652,P=0.521);但在药物A为2.5mg(drug_a=2)和5.0mg(drug_a=3)水平时,药物B各水平之间的镇痛时间差异均有统计学意义(P<0.05)。两两比较显示,当药物A为2.5mg时,药物B浓度30.0μg与5.0μg相比,镇痛时间差异有统计学意义(P=0.012),30.0μg与15.0μg相比以及15.0μg与5.0μg相比差异均无统计学意义(P>0.05)。当药物A为5.0mg时,药物B浓度30.0μg与15.0μg相比以及30.0μg与5.0μg相比,镇痛时间差异均有统计学意义(P<0.01),但15.0μg与5.0μg相比,镇痛时间差异无统计学意义(P=0.363)。
综上可知,对产妇分娩时镇痛,A、B两种药物联合运用时会相互影响,随着药物浓度的增加,联合作用趋于复杂和不稳定。
五、分析小技巧
- 正态性检验:两因素或多因素方差分析时,有两种选择来测试正态性:如果每组有较多观察数,且组别较少时,可使用原始数据检查每个组的正态性。如果有很多组,或每个组的观察数很少,可使用残差检查整体的正态性。在Stata中使用“swilk”命令可进行“Shapiro-Wilk (夏皮罗-威尔克正态性)”检验。关于正态性检验的注意事项详见文章(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。
- 方差齐性检验:两因素方差分析时,使用残差检验方差齐性。可绘制残差图(“rvfplot”命令)或使用BP(Breusch-Pagan)法(“estat hettest”命令)检验方差齐性。关于方差齐性检验的更多内容请阅读(医学统计学核心概念及重要假设检验的软件实现(4/4)——方差齐性检验及SPSS实现)。
- 交互作用判断:两因素方差分析时,需要首先判断两个因素之间是否存在交互作用。如果交互作用有统计学意义,则需要分析单独效应。此时,单纯研究某个因素的作用并无意义,应分别探讨另一个因素不同水平时对该因素的作用。当不存在交互作用时,说明两因素的作用彼此独立,逐一分析各因素的主效应即可;计算主效应时,在模型中仍需要保留交互项。
- 在上面的分析中,drug_a和drug_b取值都是1、2、3,得到的结果也是以1、2、3显示。根据案例介绍可知,药物A取3个剂量:1.0mg、2.5mg、5.0mg,对应变量drug_a的1、2、3组;药物B也取3个剂量:5.0μg、15.0μg、30.0μg,对应变量drug_b的1、2、3组。如果想要在Stata分析结果中直接显示剂量值,可使用“recode”命令。
recode drug_a (1=1 "1.0mg") (2=2 "2.5mg") (3=3 "5.0mg"), pre(new) recode drug_b (1=1 "5.0μg") (2=2 "15.0μg") (3=3 "30.0μg"), pre(new)
上述命令生成两个新变量newdrug_a(取值为1.0、2.5、5.0mg)和newdrug_b(取值为5.0、15.0、30.0μg),分别对应drug_a和drug_b,部分数据如图16所示。后续分析时使用newdrug_a和newdrug_b即可,读者可自行尝试。
