在前面文章中介绍了Kruskal-Wallis H检验的假设检验理论,本文将实例演示在Python软件中实现Kruskal-Wallis H检验的操作步骤。
关键词:Python; 非参数检验; 秩和检验; 多样本Kruskal-Wallis H检验; Kruskal-Wallis H检验; 多样本秩和检验; 事后检验
一、案例介绍
某医师对30名胆管癌患者的肿瘤直径进行了测定,其中9名患者肿瘤直径<2cm,11名患者肿瘤直径在2~3cm,10名患者肿瘤直径>3cm。同时该医生对所有患者血清中癌抗原19-9 (cancer antigens 19-9, CA19-9)水平(μg/L)进行了测定,问不同肿瘤直径的胆管癌患者CA19-9水平是否不同?部分数据见图1。本案例数据可从“附件下载”处下载。
二、问题分析
本案例的分析目的是比较三种不同肿瘤直径的胆管癌患者CA19-9水平是否不同。针对这种情况,可考虑使用Kruskal-Wallis H检验。Kruskal-Wallis H检验是基于秩次的非参数检验方法,用于检验多组间(也可以是两组)连续或有序分类变量是否存在差异。使用Kruskal-Wallis H检验,需要满足4个条件。
条件1:有一个观察变量和一个分组变量,在本案例中胆管癌患者CA19-9水平为观察变量,肿瘤直径分组为分组变量,该条件满足。
条件2:观察变量为非正态分布或方差不齐的连续变量或有序分类变量,变量的正态性或方差齐性需要通过软件分析进行判断。
条件3:存在多个分组(k≥2)。本研究中分为三组,该条件满足。
条件4:具有相互独立的观测值。本研究中各研究对象的CA19-9水平都是独立的,不存在互相干扰的情况,该条件满足。
三、软件操作及结果解读
(一) 导入数据
import pandas as pd #导入pandas包
df = pd.read_csv('多样本Kruskal-Wallis H检验.csv') #导入CSV数据
pd.set_option('display.max_rows', 10)
df #查看数据
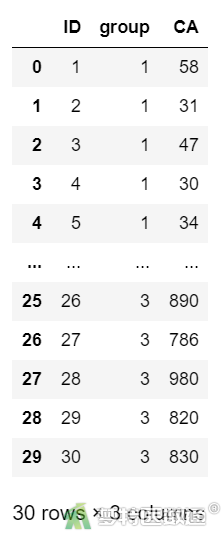
图1
在数据栏目中可以查看全部数据情况,数据集中共有3个变量和30个观察数据,3个变量分别代表被调查者的编号(ID)、组别(group)及CA19-9水平(CA)。
(二) 适用条件判断
1. 条件2判断(正态性检验)
(1) 软件操作
Kruskal-Wallis H检验时,需要分别考察每一组数据的正态性情况,因此需要拆分数据。
## 分组描述数据子集 ##
df.groupby("group").describe()

图2
## 绘制Q-Q图 ##
import statsmodels.api as sm #导入statsmodels.api包 import pylab sm.qqplot(df.loc[df.loc[:,'group']==1,'CA'], line='s') #选取第一组数据 pylab.show() #显示子集1的Q-Q图 sm.qqplot(df.loc[df.loc[:,'group']==2,'CA'], line='s') #选取第二组数据 pylab.show() #显示子集2的Q-Q图 sm.qqplot(df.loc[df.loc[:,'group']==3,'CA'], line='s') #选取第三组数据 pylab.show() #显示子集3的Q-Q图
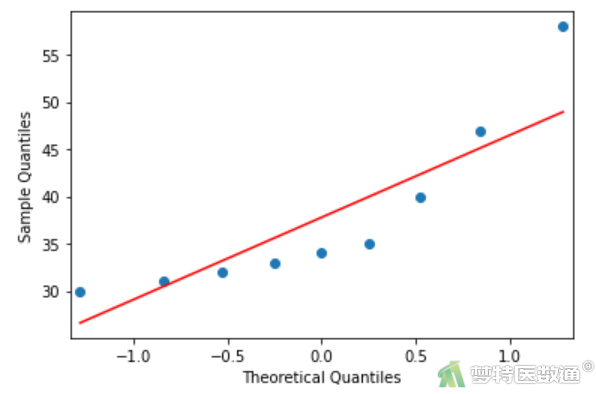
图3-1
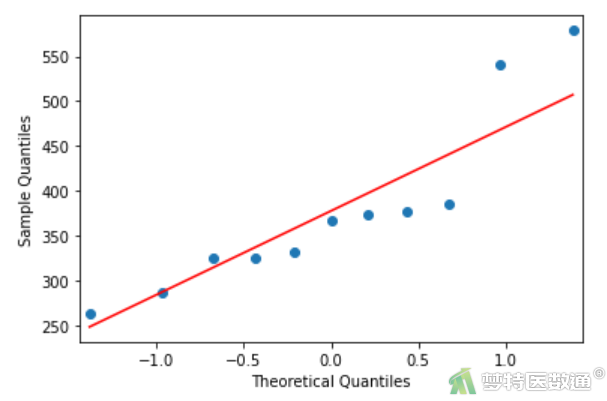
图3-2
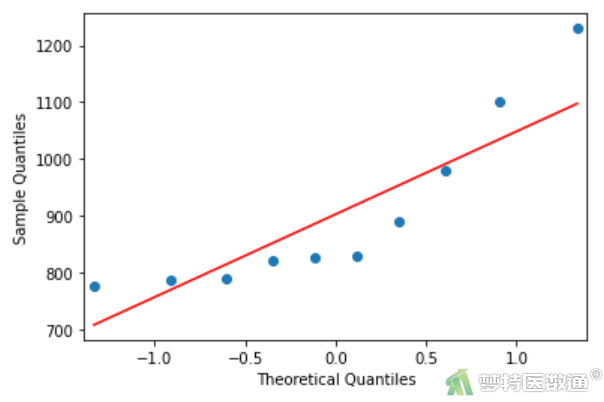
图3-3
## 正态性检验 ##
from scipy import stats #导入scipy包 shapiro_test1 = stats.shapiro(df.loc[df.loc[:,'group']==1,'CA']) print(shapiro_test1) shapiro_test2 = stats.shapiro(df.loc[df.loc[:,'group']==2,'CA']) print(shapiro_test2) shapiro_test3 = stats.shapiro(df.loc[df.loc[:,'group']==3,'CA']) print(shapiro_test3) #分组进行Shapiro-Wilk正态性检验

图4
(2) 结果解读
Q-Q图(图3-1、图3-2和图3-3)上散点偏离对角线较远,提示三组数据不服从正态分布;Shapiro-Wilk正态性检验结果(图4)显示三组的P值分别为0.02283、0.03485和0.0165,均<0.1,也提示三组数据不服从正态分布。关于正态性检验的注意事项详见文章正态性假设检验(Normality Hypothesis Test)——SPSS软件实现。
2. 条件2判断(方差齐性检验)
(1) 软件操作
## levene法方差齐性检验 ##
group0 = df.loc[df.loc[:,'group']==1]['CA'] #选取第一组数据 group1 = df.loc[df.loc[:,'group']==2]['CA']#选取第二组数据 group2 = df.loc[df.loc[:,'group']==3]['CA'] #选取第二组数据 leveneTestRes = stats.levene(group0, group1, group2, center='mean') #levene法齐性检验 print(leveneTestRes) #显示检验结果

图5
(2) 结果解读
“describe (描述性分析)”结果(图2)显示,肿瘤直径<2cm组、2~3cm组、>3cm组的std (标准差)分别为9.24、98.18和153.86,三组之间标准差存在较大差异,但还需要依据统计学检验的结果进行判断。
“Levene’s”方差齐性检验结果(图5)显示F=7.1921,P=0.003134<0.1,提示三组数据方差不齐。
综上,本案例中三组连续变量数据既不服从正态分布,也不满足方差齐性,可以考虑使用Kruskal-Wallis H检验。
(三) 整体检验
1. 软件操作
## Kruskal-Wallis H检验 ##
from scipy import stats stats.kruskal(group0, group1, group2) #Kruskal-Wallis检验

图6
2. 结果解读
(1) 统计描述
“describe (描述性分析)”结果(图2)提供了三组数据的“mean (均数)”、“std (标准差)”、“min (最小值)”、“25%(下四分位数)”、“50% (中位数)”、“75% (上四分位数)”和“max (最大值)”。可知,肿瘤直径<2cm的患者CA19-9水平为34.00 (P25~P75:32.00~40.00) μg/L,肿瘤直径2~3cm的患者CA19-9水平为367.0 (P25~P75:325.0~381.0) μg/L,肿瘤直径>3cm的患者CA19-9水平为828.0 (P25~P75:796.8~957.5) μg/L。三组的CA19-9值目测存在差异,但还需要依据统计学检验的结果进行判断。
(2) 统计学推断
Kruskal-Wallis 秩和检验结果(图10)显示χ2=25.748,P<0.001,可认为三种不同肿瘤直径的胆管癌患者的CA19-9水平不全相同(至少存在两组不相同)。
(四) 事后检验(两两比较)
虽然得到了“三种不同肿瘤直径的胆管癌患者的CA19-9水平不全相同”的结论,但我们仍然不清楚到底是哪两组之间不同,因此需要进一步两两比较。
1. 软件操作
## 事后两两比较 ##
import scikit_posthocs as sp import numpy as np data = np.array([group0, group1, group2]) sp.posthoc_dunn(data, p_adjust='holm') #事后检验
注:若未安装“scikit_posthocs”包,需要先安装该包,代码为:
! pip install scikit_posthocs

图7
2. 结果解读
“Dunn检验” (Holm-Sidak多重t检验的非参数模拟)结果(图7)提供了不同肿瘤直径胆管癌患者CA19-9水平两两比较的P值。可知,肿瘤直径<2cm的患者CA19-9水平和肿瘤直径2~3cm的患者CA19-9水平差异有统计学意义(P=0.013),肿瘤直径2~3cm的患者CA19-9水平和肿瘤直径>3cm的患者CA19-9水平差异有统计学意义(P=0.013),肿瘤直径<2cm的患者CA19-9水平和肿瘤直径>3cm的患者CA19-9水平差异有统计学意义(P<0.001)。
四、结论
本研究采用Kruskal-Wallis H检验判断不同肿瘤直径的胆管癌患者CA19-9水平是否不同。通过Q-Q图和Shapiro-Wilk检验,提示三组数据不服从正态分布;通过Levene’s检验,提示三组数据总体方差不齐,符合使用Kruskal-Wallis H检验的条件。
结果显示,肿瘤直径<2cm、2~3cm和>3cm的患者CA19-9水平分别为34.00 (P25~P75:32.00~40.00) μg/L、367.0 (P25~P75:325.0~381.0) μg/L和828.0 (P25~P75:796.8~957.5) μg/L。Kruskal-Wallis H检验结果显示,三种不同肿瘤直径的胆管癌患者的CA19-9水平不全相同(χ2=25.748,P<0.001)。两两比较显示,不同肿瘤直径的胆管癌患者CA19-9水平均不相同。
五、知识小贴士
- 两独立样本资料的非参数检验,既可以采用Wilcoxon秩和检验,也可以采用Kruskal-Wallis H检验,两者检验结论一致。
- 对于多组定量资料比较,在符合正态性和方差齐性的条件下,首选使用单因素方差分析。对于不是特别严重的方差不齐,可使用单因素方差分析的校正检验方法(Welch one-way ANOVA/ Welch’s F检验);但当组间方差差异较大时,建议使用非参数检验(Kruskal-Wallis H检验)。如果数据正态性和方差齐性都不满足,最好使用非参数检验(Kruskal-Wallis H检验)。