简单线性回归分析(Simple Linear Regression Analysis)——Python软件实现

关键词：Python; 简单线性回归; 直线回归; 残差齐性检验; 残差正态检验

一、案例介绍

研究健康成年人的体重和双肾脏总体积(ml)的关系，测得24名健康成年人的体重wt (kg)与双肾脏总体积volume (ml)，拟探讨健康成年人的体重与双肾总体积是否有关，并希望通过健康成年人的体重预测双肾总体积。部分数据见图1。本案例数据可从“附件下载”处下载。

二、问题分析

本案例的分析目的是通过判断两个计量资料之间的关系，同时使用其中一个变量预测另一个变量，计算其中一个变量对另一个变量变异的解释程度。针对这种情况，可以使用简单线性回归分析。但需要满足6个条件：

条件1：因变量为连续变量。本研究中，健康成年人的体重为连续变量，该条件满足。

条件2：若自变量是连续变量，则与因变量之间存在线性关系。该条件需要通过软件分析后判断。

条件3：各观测值之间相互独立，即残差之间不存在自相关。通过研究设计和数据收集的过程分析，可判断本案例中观测值之间不存在互相影响的情况。该条件还可通过软件分析后辅助判断。

条件4：自变量不存在显著的异常值，该条件需要通过软件分析后判断。

条件5：残差符合正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件6：残差方差齐。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

import pandas as pd
df = pd.read_csv(‘简单线性回归.csv’)  #导入CSV数据
df #查看数据

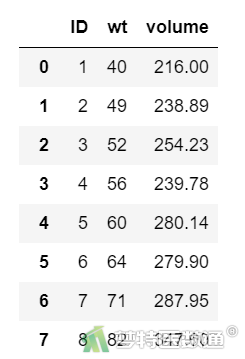
在数据栏目中可以查看全部数据情况，数据集中共有3个变量和24个观察数据，3个变量分别代表编号(ID)、体重(wt)与双肾脏总体积(volume)。

如果数据集较大也可使用如下命令查看数据框结构，输出结果见图2。

df.info()  #查看数据框结构

(二) 适用条件判断

1. 条件2判断(因变量和自变量之间存在线性关系)

(1) 软件操作

##线性关系判断 ##

import seaborn
import matplotlib.pyplot as plt #导入matplotlib中的pyplot绘制散点图
import numpy as np
wt = list(np.ravel(df.loc[:,['wt']].to_numpy().tolist())) #传入wt数据
volume = list(np.ravel(df.loc[:,['volume']].to_numpy().tolist())) #传入volume数据
seaborn.lmplot(x='wt',y='volume',data=df) #绘制散点图
plt.show() #显示散点图

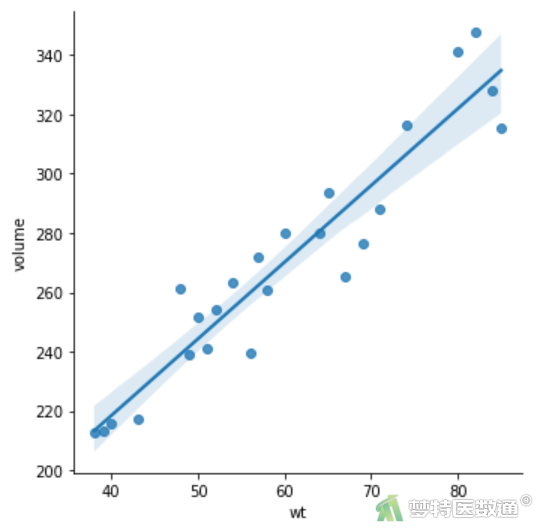
(2) 结果解读

由散点图(图3)可见，散点大致呈一条直线，提示变量“wt”和“volume”存在线性关系，该条件满足。

2. 条件3判断(各观测值之间相互独立)

Durbin-Watson自相关检验通常用来检测残差是否存在自相关，Durbin-Watson检验值分布在0~4之间，越接近2，观测值相互独立的可能性越大。需要注意的是，判断观测值是否独立，主要取决于研究设计和数据收集阶段的质量控制，Durbin-Watson检验最好用于辅助判断。

(1) 软件操作

##判断独立性 ##

from statsmodels.formula.api import ols
lm = ols('volume ~ wt', data=df).fit() #自相关检验
from statsmodels.stats.stattools import durbin_watson
test=durbin_watson(lm.resid,axis=0)
test #Durbin-Watson检验值

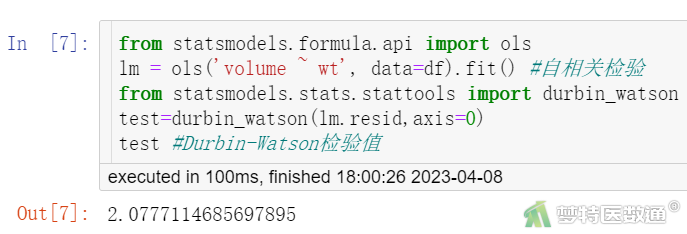
(2) 结果解读

Durbin-Watson自相关检验结果(图4)显示，DW-Statistic为2.078，说明观测值相互独立，本研究数据满足条件3。

3. 条件4判断(异常值检测)

通过散点图(图3)可见，数据不存在异常值。但仍需要统计分析结果的判断。Cook’s distance (库克距离) 用来判断强影响点是否为因变量的异常值点。一般认为当Cook’s distance <0.5时不是异常值点，当Cook’s distance >0.5时认为是异常值点。

(1) 软件操作

##计算Cook’s distance ##

inf = lm.get_influence()
cook_d = inf.cooks_distance[0] #计算Cook’s distance
print(max(cook_d)) #显示最大Cook’s distance

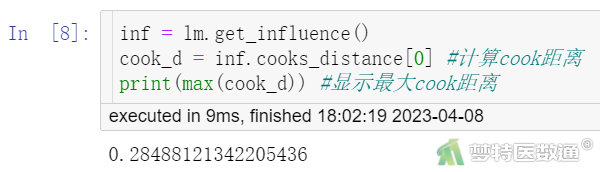
(2) 结果解读

“Cook’s distance”结果(图5)显示，最大Cook’s distance为0.285<0.5，提示不存在显著异常值，本研究数据满足条件4。

4. 条件5判断(残差正态性检验)

(1) 软件操作

## 正态性检验 ##

from scipy.stats import shapiro
shapiro(lm.resid)

import statsmodels.api as sm
y = df['volume']
lm = ols('volume ~ wt', data=df).fit() #自相关检验
results = pd.DataFrame({'index': y, #y实际值
'resids': lm.resid, #残差
'std_resids': lm.resid_pearson, #方差齐标准后的残差
'fitted': lm.predict()}) #y预测值
qqplot = sm.qqplot(results['std_resids'], line='s') #绘制qq图
plt.show(qqplot)

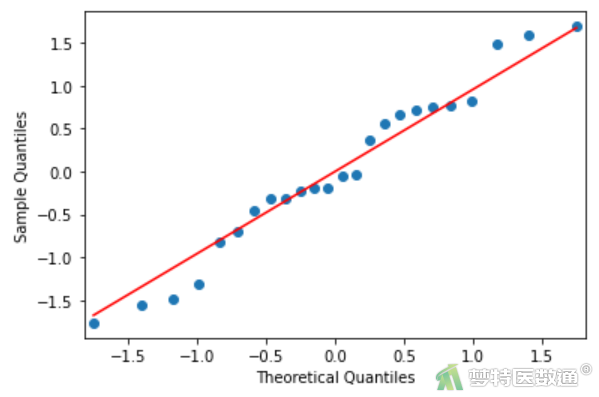
(2) 结果解读

Shapiro-Wilk正态性检验结果(图6)显示，P=0.5059>0.1，提示残差服从正态分布。残差的Q-Q图(图7)中各散点基本围绕对角线分布，也提示残差服从正态分布，本研究数据满足条件5。

5. 条件6判断(残差的方差齐性检验)

(1) 软件操作

##残差图 ##

results = pd.DataFrame({'index': y, #y实际值
'resids': lm.resid, #残差
'std_resids': lm.resid_pearson, #方差齐标准后的残差
'fitted': lm.predict()}) #y预测值
import seaborn as sns
sns.residplot(results['index'],lm.resid)
plt.show()
sns.residplot(df.loc[:,'volume'],lm.resid, color="pink")
plt.show()
sns.residplot(df.loc[:,'wt'],lm.resid, color="orange")
plt.show()

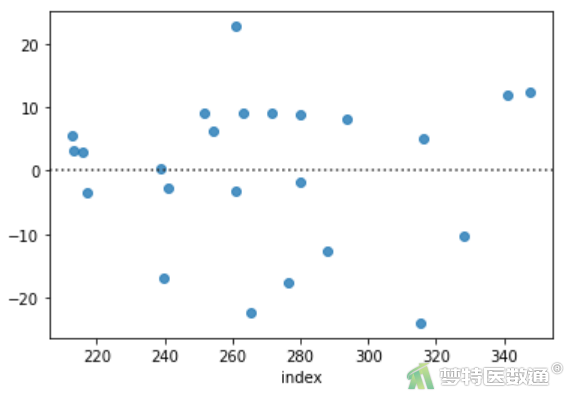
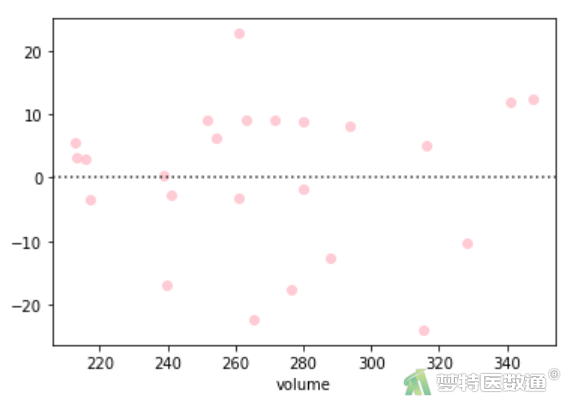
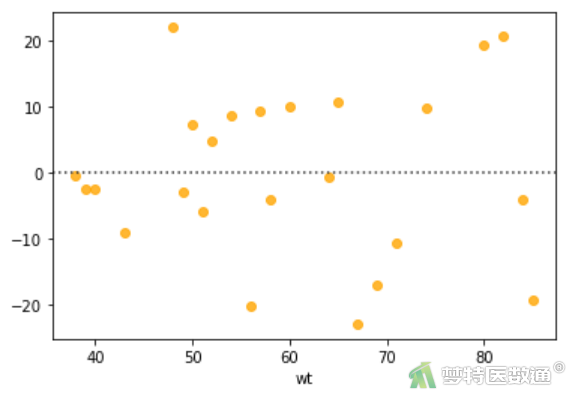
(2) 结果解读

预测值和各变量值的残差(图8~图10)分布较为均匀，并未出现特殊的分布形式(如漏斗或者扇形)，提示残差的方差齐，本研究数据满足条件6。

(三) 模型拟合

1. 软件操作

##查看模型拟合情况 ##

lm.summary()

2. 结果解读

(1) 模型拟合程度

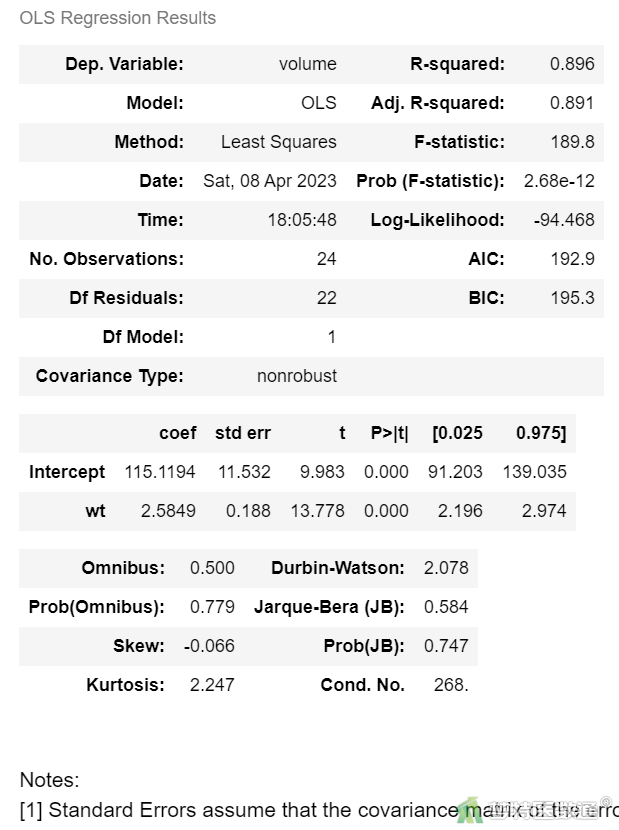
拟合后模型的各项参数见图11。

决定系数R²=0.896，提示自变量 (体重)可以解释89.6%的因变量的变异 (双肾总体积)，但是R²会受自变量个数的影响，夸大自变量对因变量变异的解释程度，自变量越多，R²越大。Adj. R² (Adjusted R²)调整了自变量个数对结果的影响，一般小于R²。Adj. R²=0.891，提示自变量 (体重)可以解释89.1%的因变量的变异 (双肾总体积)。

整体模型检验结果显示F=189.8，P<0.001，提示回归模型有统计学意义。如果P>0.05，则说明回归模型没有统计学意义。

(2) 回归系数解释

回归模型的截距(Intercept)为115.1194，表示自变量取值为0时，因变量的取值，并无实际专业意义；变量“wt”的非标准化系数(即斜率)为2.5849，表示体重每增加1 kg，双肾体积增加2.5849 ml。据此可以写出本案例的回归方程为：

Volume =115.1194+2.5849×wt

根据此方程可以计算合理范围内体重对应的双肾总体积。

四、结论

本研究采用简单线性回归模型通过健康成年人的体重预测双肾总体积。通过绘制散点图，提示两者之间存在线性关系；通过专业判断和Durbin-Watson检验提示数据之前相互独立；通过绘制散点图和库克距离分析，提示数据不存在需要删除的异常值；通过Shapiro-wilk检验及绘制残差Q-Q图，提示残差符合正态分布；通过绘制残差图，提示残差方差齐。本研究数据满足线性回归分析条件。

线性回归分析方程为：volume = 115.1194 + 2.5849×wt，回归模型具有统计学意义，F=189.8，P<0.001；自变量(体重)可以解释89.6%的因变量的变异(双肾总体积)，影响程度较高(adjusted R²=0.8914)，即体重每增加1kg，双肾总体积增加2.5849ml。

五、分析小技巧

(一) 各观测值之间独立性检验

判断观测值是否独立，主要取决于研究设计和数据收集阶段的质量控制，Durbin-Watson检验最好用于辅助判断。Durbin-Watson检验值分布在0~4之间，越接近2，观测值相互独立的可能性越大。

(二) 异常值检测

Cook’s distance (库克距离)用来判断强影响点是否为因变量的异常值点。一般认为当Cook’s distance <0.5时不是异常值点，当Cook’s distance >0.5时认为是异常值点。

并非所有的异常点都意味着结果不好，有时候发现异常点可能会提示有更重要的信息。如果出现异常点，首先应检查数据是否录入错误，也可以选择其他相应模型来拟合，或者需要收集更多的数据来证实。

(三) 残差正态性检验

如果残差不符合正态分布，可以考虑对因变量进行数据变换，使其服从正态分布后再拟合线形回归模型，也可采用非参数回归。

(四) 残差的方差齐性检验

残差的方差齐是指在自变量取值范围内，对于任意自变量取值，因变量都有相同的方差。线形回归中，残差的方差齐实际上要比残差正态分布重要。如果这一条件不满足，可对因变量进行变量变换，使其满足残差方差齐，也可以采用加权回归分析，消除方差的影响。

(五) 回归模型

分析中得到的回归截距，是当自变量为0时因变量对应的值。在本研究中，回归截距为当体重为0时，研究对象的双肾总体积为115.119 ml。这显然不符合客观实际，因此无论截距的检验结果是否有统计学意义，一般都不必过多关注，在进行简单线性回归时更多关注的是斜率。在进行回归分析时，要注意避免对数据的过度挖掘，不能将回归模型分析的结果随意延伸到自变量取值范围以外的数值。也不能随意将模型分析结果延伸到因果关系。