对于许多统计学检验,都要求连续性变量所对应的总体服从正态分布。但由于总体未知或未能获取,所以实际数据分析过程中是通过考察样本的正态分布情况来判断总体正态性,如单样本t检验要求样本服从(近似)正态分布,独立样本t检验要求两组样本均服从(近似)正态分布,配对样本t检验要求两组差值服从(近似)正态分布等。本文将实例演示正态分布检验在R软件中的实现步骤。
关键词:R; 正态性检验; 正态分布; Kolmogorov-Smirnov检验; Shapiro-Wilk检验; Q-Q图
一、案例介绍
某研究者使用单样本t检验比较特殊作业成年男性工人血红蛋白与正常成年男性血红蛋白含量均数是否相等。研究过程中测量了52名特殊作业成年男性工人的血红蛋白含量,试分析这52名特殊作业成年男性工人的血红蛋白含量值是否服从正态分布?部分数据见图1。本案例数据可从“附件下载”处下载。
data <- read.csv("正态分布检验.csv")
View(data)
二、图示法(以Q-Q图为例)
Q-Q图是一种散点图,对应于正态分布的Q-Q图就是由标准正态分布的分位数为横坐标,样本值为纵坐标的散点图。
要利用Q-Q图鉴别样本数据是否服从正态分布,可根据该Q-Q图上的点是否近似地分布于直线附近进行判断。
(一) 软件操作
语句如下,结果见图2。
qqnorm(data$Hb) #绘制QQ图 qqline(data$Hb) #增加趋势线

(二) 结果解读
由图2可见数据点基本围绕着斜线分布,提示数据呈现(近似)正态分布。
三、检验法
(一) K-S检验
柯尔莫戈洛夫-斯米诺夫检验(Kolmogorov-Smirnov test),简称K-S检验,一般适用于大样本。
1. 软件操作
语句如下,结果见图3。
library(nortest) lillie.test(data$Hb)
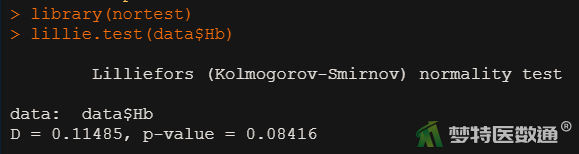
2. 结果解读
从图3结果可知P=0.08416>0.05,可认为该组数据近似服从正态分布。
(二) S-W检验
S-W检验,即Shapiro-Wilk检验,适用于小样本。
1. 软件操作
语句如下,结果见图4。
shapiro.test(data$Hb)
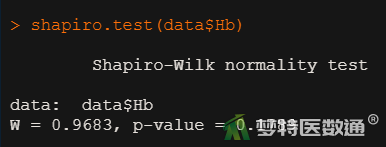
2. 结果解读
由图4可知,W=0.9683, P>0.1789,提示数据服从正态分布。
四、正态性检验的注意事项
- 关于正态性检验的更多内容详见正态性假设检验(Normality Hypothesis Test)——SPSS软件实现。
- 关于正态性转换的更多内容详见正态性转换(Normality Transformation)——SPSS软件实现。
End