在前面文章中,以实例讲解了医学数据分析过程中正态性检验的SPSS实现过程及注意事项。许多统计学分析方法使用的前提是数据总体服从(近似)正态分布,若实际数据不服从正态分布的假定,尤其是小样本资料,仍然使用原始数据进行分析而得到的结果可能会与真实结果相差较远。此时,可以对明显非正态分布的资料进行适当转换,以使数据满足统计分析方法对资料分布的要求。在本篇文章中,将介绍几种常见的正态性转换方法,举例演示部分方法在SPSS中的操作过程并总结数据正态性转换的注意事项。
关键词:SPSS; 正态性转换; 对数变换; Box-Cox变换; 正态得分法
一、数据分布特征
做正态性转换之前,需要先大致了解数据分布的特征,其中偏度和峰度是计量资料两个重要的特征。
(一) 偏度(Skewness)
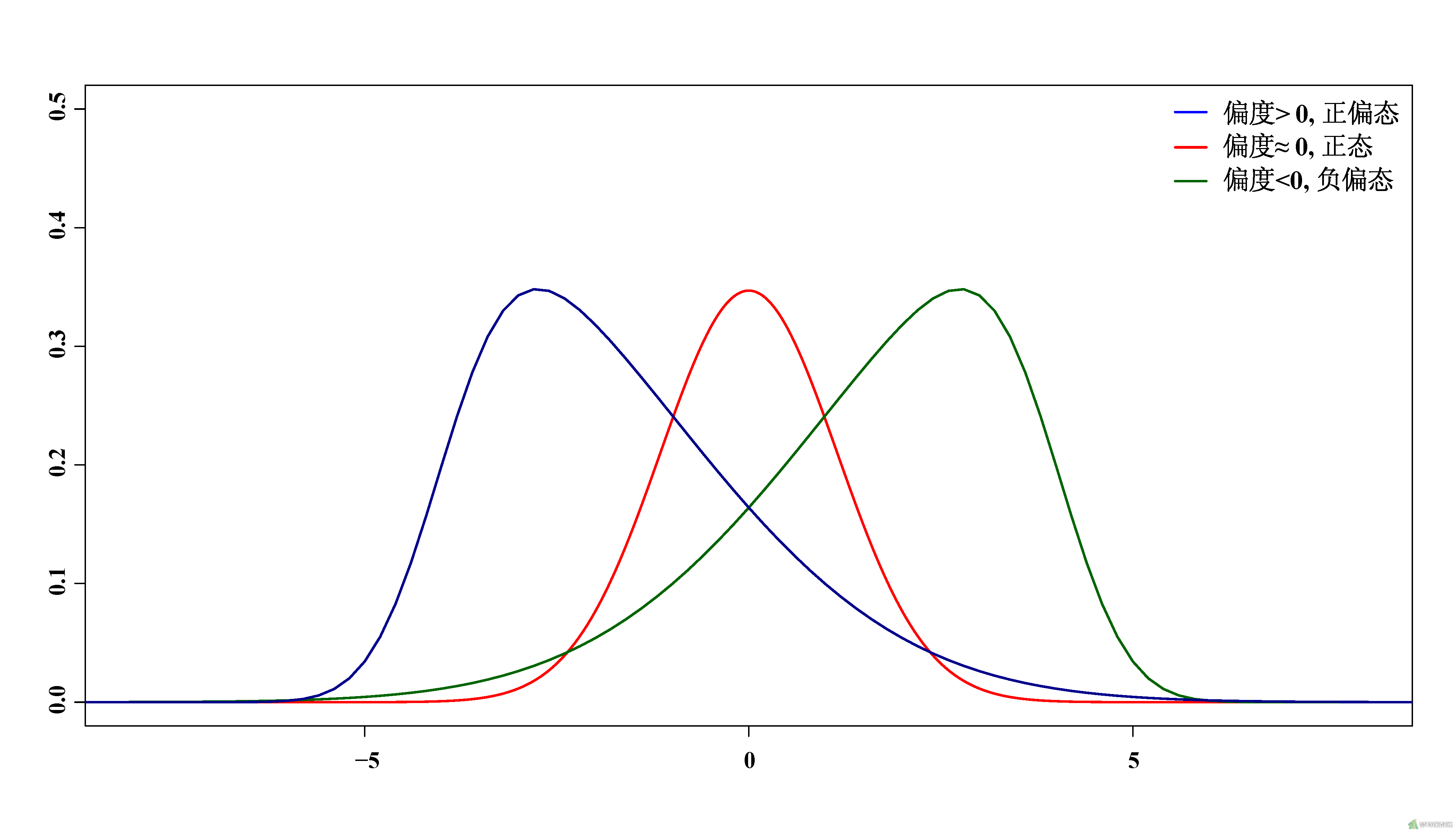
偏度是描述数据分布不对称方向及其程度的指标,样本偏度g1=0时,可认为分布是对称的,服从正态分布;当g1>0时,分布为右偏,即拖尾在右边,峰尖在左边,也称为正偏态;当g1<0时,分布为左偏,即拖尾在左边,峰尖在右边,也称为负偏态。见图1。
(二) 峰度(Kurtosis)
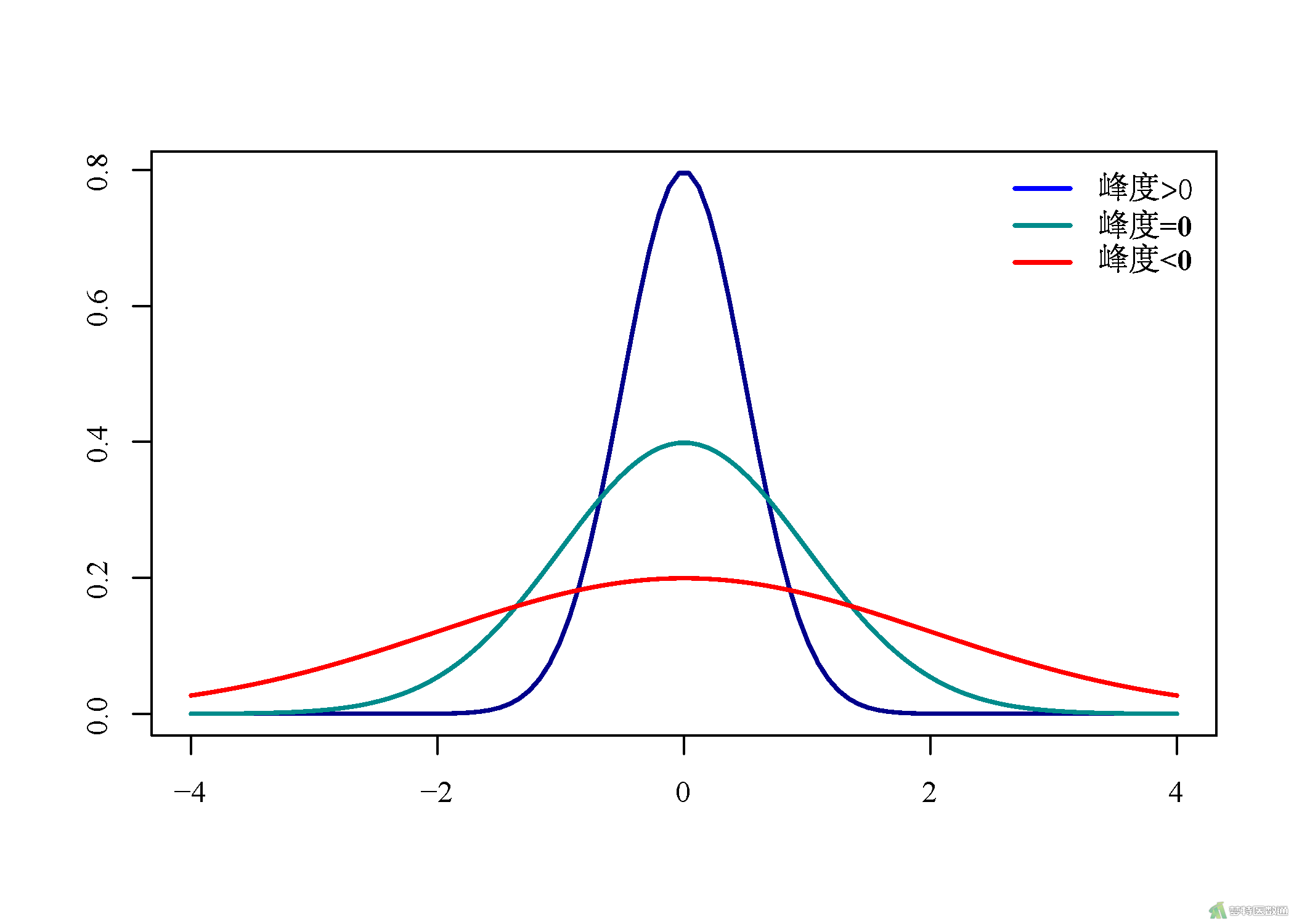
峰度是描述数据分布形态陡缓程度的指标,当g2=0时,可认为分布的峰态合适,服从正态分布(不胖不瘦);当g2>0时,分布的峰态陡峭(高尖);当g2<0时,分布的峰态平缓(矮胖)。见图2。
二、常用正态性转换方法
(一) 对数变换(logarithmic transformation)
即将原始数据X取对数(常用对数或自然对数),常用形式如下:
X' = lgX
X' = lg(X+1),适合原始数据较小或有0时
X' = lg(X+K)或X' = lg(K-X)
对数变换适用于:①服从对数正态分布的资料(原始数据的效应是相乘时),如抗体滴度,食品、蔬菜、水果中农药残留量,环境中某些有毒有害物质的含量,某些疾病的潜伏期资料等;②部分正偏态分布资料;③各组的均数与标准差成比例或变异系数接近的资料。
(二) 平方根变换(square root transformation)
即将原始数据X开平方根,常用形式如下:
\(X^{\prime}=\sqrt{X}\)\( X^{\prime}=\sqrt{X+0.5}\) 或 \( X^{\prime}=\sqrt{X+1} \) ,适合原始数据较小或有0时
平方根变换适用于:①服从Poisson分布的资料,即各样本方差与均数近似相等的资料,如放射性物质在单位时间内的放射次数,某些发病率较低的疾病在时间或地域上的发病例数等资料;②轻度偏态分布资料;③样本方差与均数呈正相关的资料;④观察单位为率,取值在0%~20%或80%~100%的资料。
(三) 平方根反正弦变换(arcsine transformation)
即将原始数据X的平方根取反正弦变换,基本形式如下:
用角度表示: \( X^{\prime}=\sin ^{-1} \sqrt{X} \)
用幅度表示: \( X^{\prime}=\left(\frac{\pi}{180}\right) \sin \sqrt[-1]{X} \) ,其中π为圆周率
平方根反正弦变换适用于个体观察指标为比值或百分比的资料,如淋巴细胞转变率(%)、白细胞分类计数百分比(%)等。
(四) 平方变换(square transformation)
即将原始数据X的平方作为分析数据。基本形式如下:
X' = X2
平方变换常用于方差与均数呈反比时或资料呈左偏态分布时。
(五) 倒数变换(reciprocal transformation)
即将原始数据X取倒数,基本形式如下:
X' = 1/X
倒数变换适用于数据两端波动较大的资料,或方差与均数的平方呈正比时,并且往往要求资料中没有接近或小于0的数据。
(六) Box-Cox变换
Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法,是统计建模中常用的一种数据变换,用于连续计量资料的因变量不满足正态分布的情况。Box-Cox变换是对因变量(Y)进行变换,Y的变换方式是由可变参数λ决定的。其变换形式为:
\(Y(\lambda)=\left\{\begin{array}{ll}\frac{Y^{\lambda}-1}{\lambda}, & \lambda \neq 0 \\\ln Y, & \lambda=0\end{array}\right.\)
Box-Cox变换可以明显地改善数据的正态性、对称性和方差齐性,对许多数据都适用。
(七) 正态得分法(normal score method)
是直接将数据排序,然后结合标准正态分布对每个位置的数据重新赋值,从而实现正态性转换。
三、正态性转换的SPSS实现
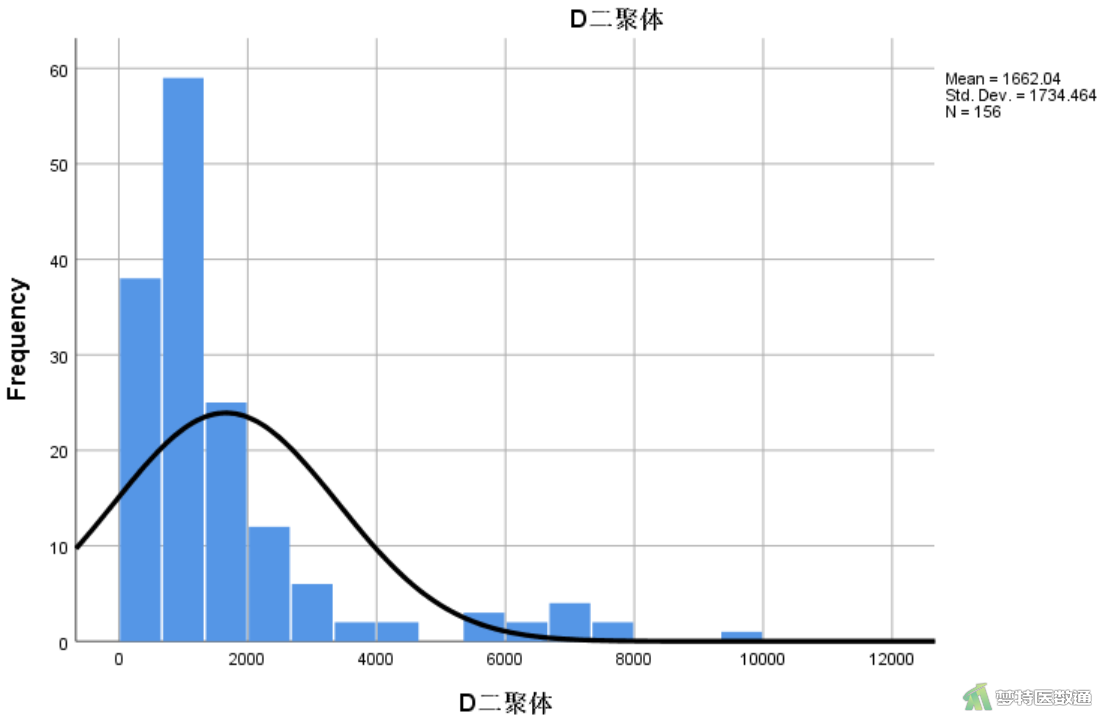
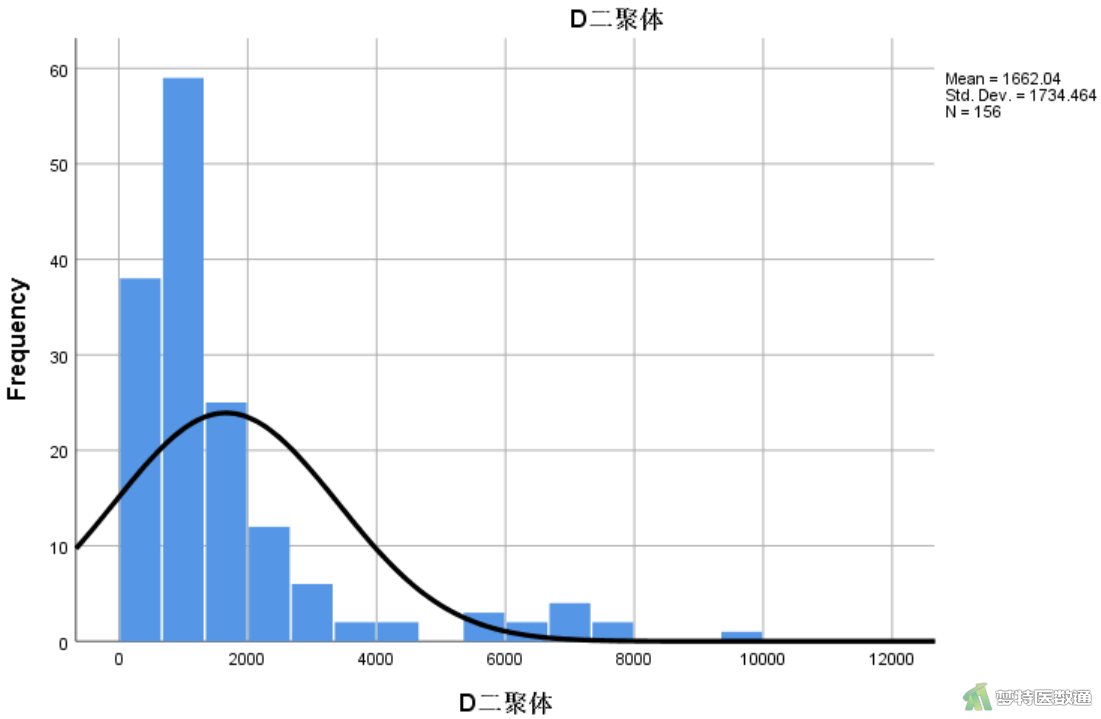
此处仍以前面文章中的实例介绍在SPSS软件中进行正态性转化的操作步骤,多种正态性检验方法均提示变量“D-二聚体”的浓度不服从正态分布,呈现正偏态分布(图3)。下面,根据常用正态性变换的适用范围,使用对数变换和正态得分法尝试对该变量进行正态性转换。
(一) 对数变换
1. 软件操作
①选择“Transform(转换)”—“Compute Variable(计算变量)”(图4)。

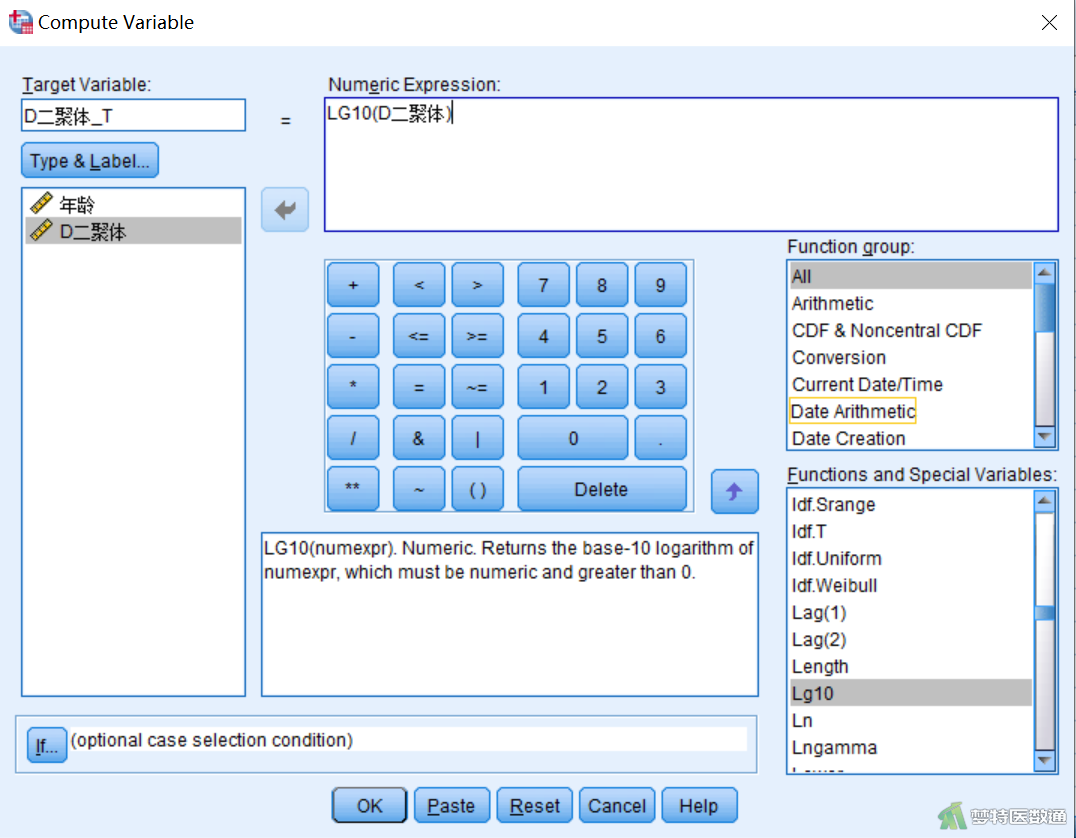
②在“Compute Variable(计算变量)”子对话框中,在“Target Variable(目标变量)”中输入“D二聚体_T”(表示转换后新变量的名称);点击“Function group(功能函数)”中的“All(全部)”后,在“Functions and Special Variables(功能和具体函数)”中选择“Lg10”后双击,将其调入“Numeric Expression(数值表达式)”,再双击变量“D二聚体”,将其调入“LG10()”的()中,生成“LG10(D二聚体)”公式(图5),点击OK。
③在数据视图中新生成了转换后的变量“D二聚体_T”(图6)。
④选择“Analyze(分析)”—“Descriptive Statistics(描述统计)”—“Explore(探索)”(图7)。
⑤在“Explore(探索)”子对话框中,将变量“D二聚体_T”选入“Dependent List(因变量列表)”(图8),然后点击“Plots(图)”。
⑥在“Plots(图)”子对话框中勾选“Histogram(直方图)”和“Normality plots with tests(含检验的正态图)”(图9),点击“Continue(继续)”,然后点击OK。
2. 结果解读
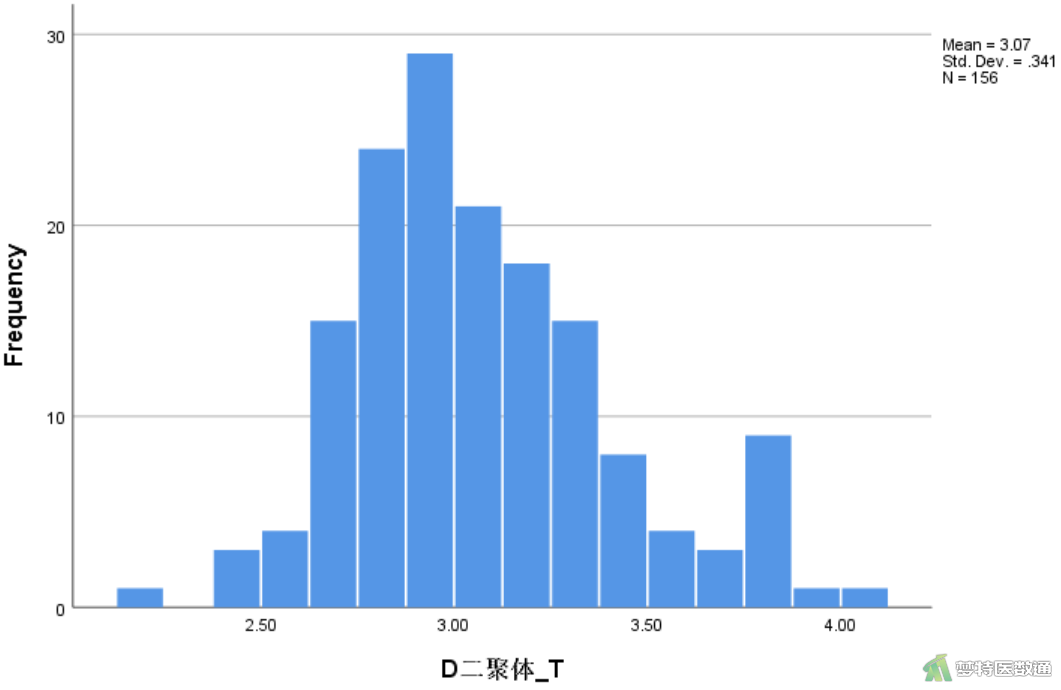
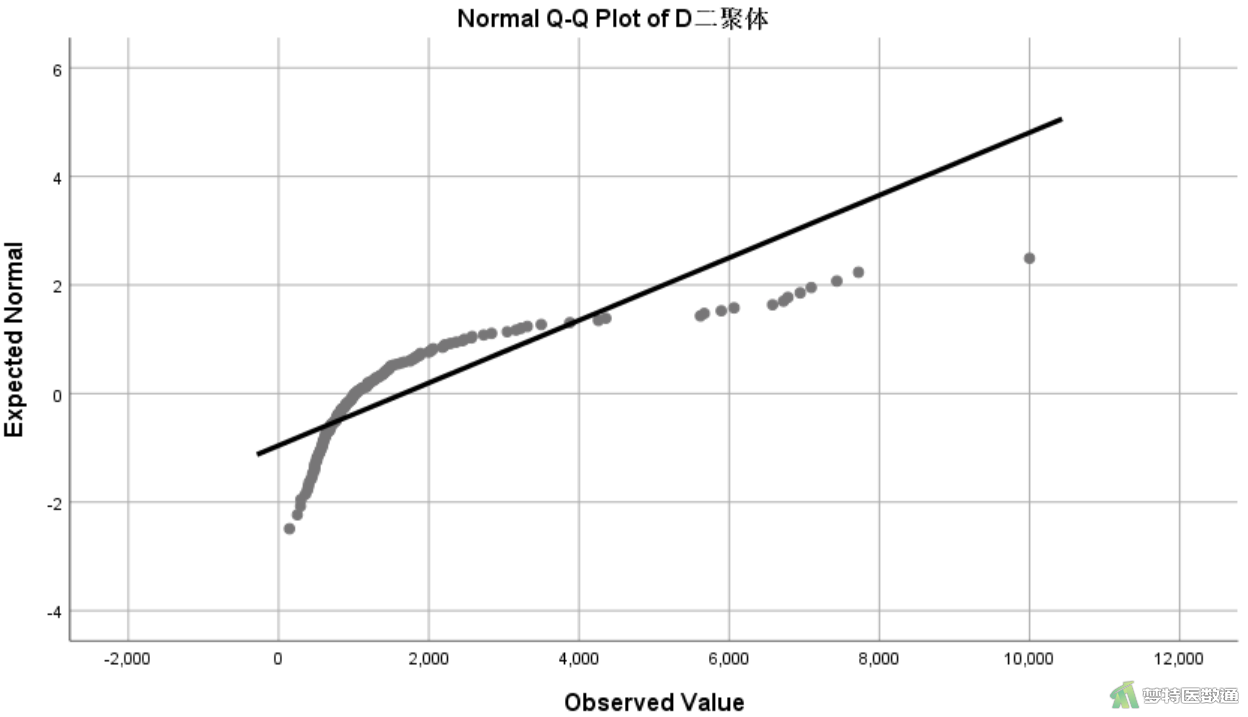
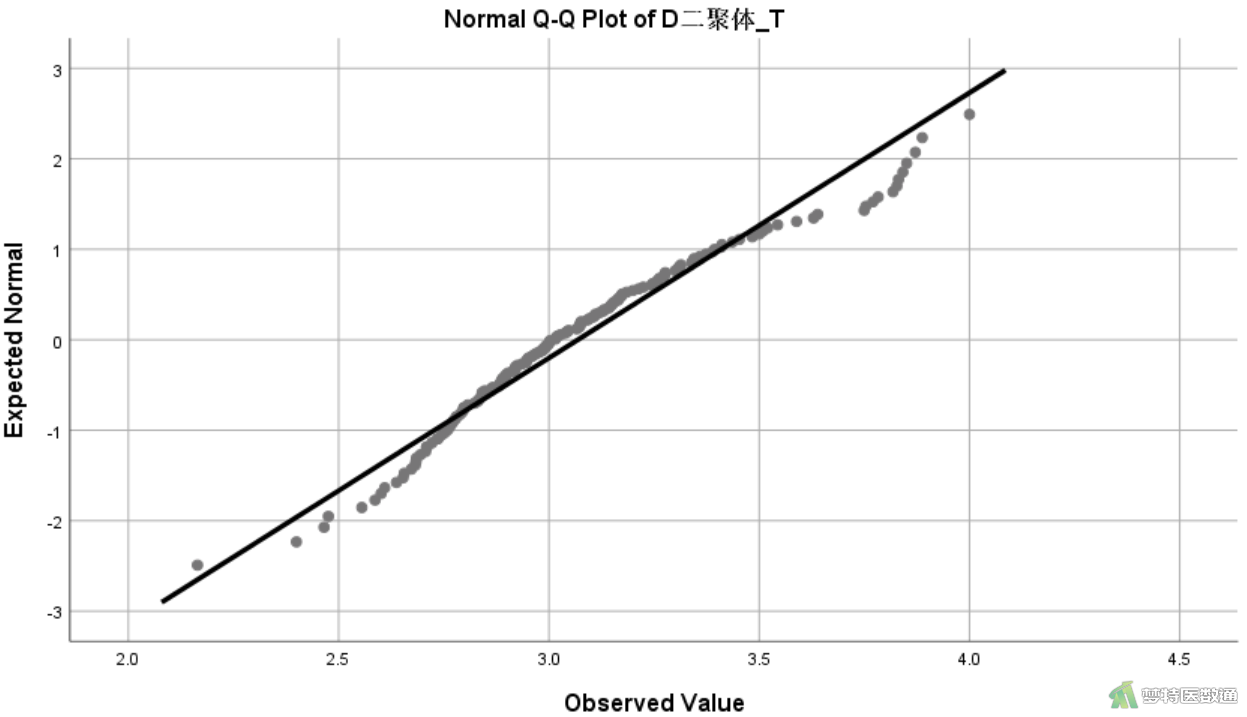
图10的Shapiro-Wilk检验(S-W检验)显示P<0.001,提示数据转换后还不服从正态分布,但对比转换前后的直方图(图3与图11)和转换前后的Q-Q图(图12和图13)可知经过转换的变量分布情况已经得到了明显改善,呈现近似正态分布。关于正态性检验的注意事项详见文章(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。

(二) 正态得分法
1. 软件操作
①选择“Transform(转换)”—“Rank Cases(个案排秩)”(图14)。
②在“Rank Cases(个案排秩)”子对话框中,将“D二聚体”选入“Variable(变量)”对话框(图15),然后点击“Rank Cases: Types(个案排秩类型)”。
③在“Rank Cases: Types(个案排秩类型)”子对话框中,勾选“Normal scores(正态得分)”,“Proportion Estimation Formula(比例估计公式)”可以默认“Blom”,也可以选择其他三个(图16),点击“Continue(继续)”,然后点击OK。
④在数据视图中新生成了转换后的变量“ND二聚”(图17),参照图7-图9的操作检验变量“ND二聚”的正态性情况。
2. 结果解读
图18的Shapiro-Wilk检验(S-W检验)显示P=1.000>0.1,提示数据转换后服从正态分布,从图19的直方图和图20的Q-Q图也可知变量在转换后服从正态分布。

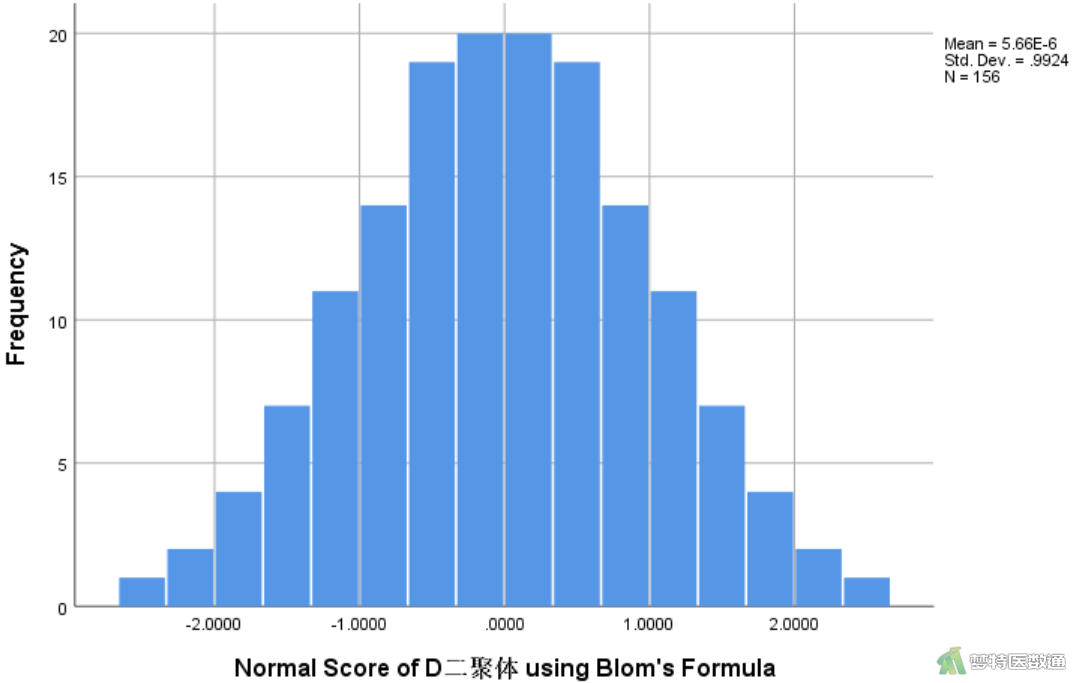
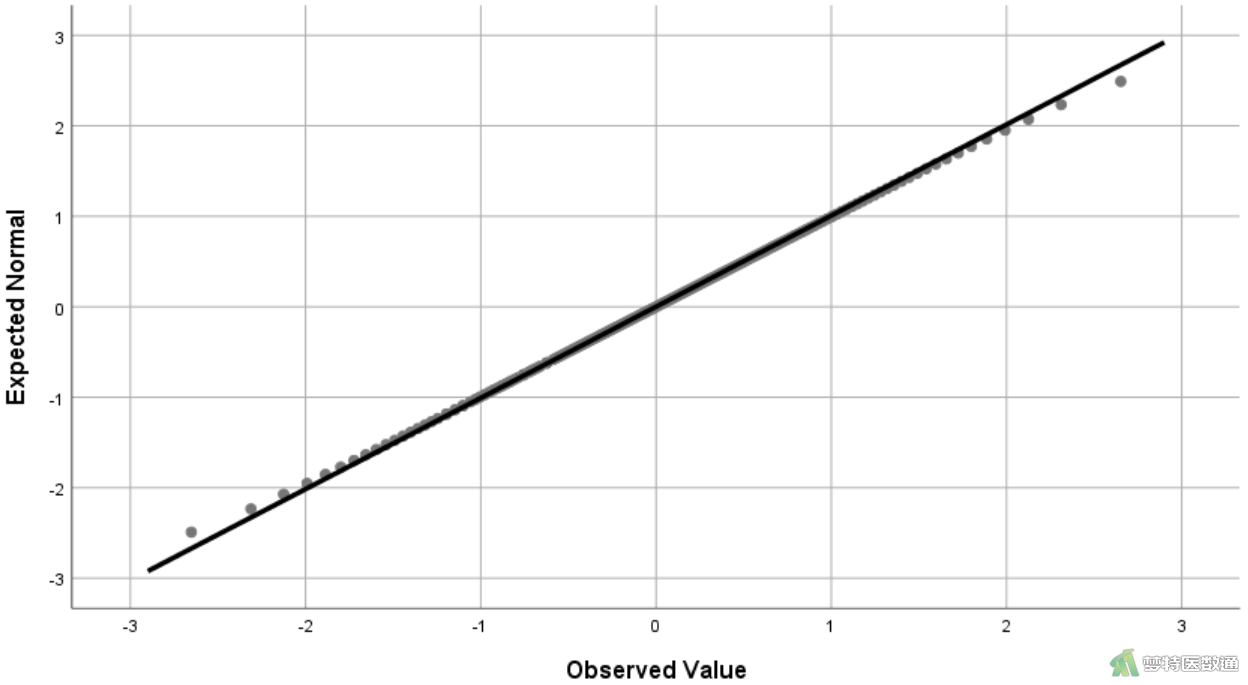
四、数据正态性转换的注意事项
(一)正态性转换方法的选择
正态性转换前需要先对数据的分布情况进行大致判断,然后尝试选择合适的转换方法。需要注意的是,正态性转换只是有可能改善数据的正态分布情况,并不一定能满足正态性要求;此外不合适的转换方法可能会造成过度转换,也有可能反而会加剧非正态情况。因此可以尝试多种正态性转换方法,从中选择效果较好者,并且需要对转换后变量的分布情况重新进行检验。如果通过多种转换方法依然无法达到较为理想的效果,此时最好放弃使用基于正态性分布为前提的统计学分析方法(如t检验、方差分析),可选择适合非正态分布数据的方法(如非参数检验)进行数据分析。
(二)同时对多组数据进行正态性转换
在进行两独立样本t检验、方差分析等方法时,要求每组数据均呈正态分布,因此当出现某一组数据正态,另一组数据非正态时,需要同时对多组数据进行正态性转换。
(三)正态性转换后要重新进行变量间的关系检验
在进行相关分析或线性回归时,要求自变量与因变量之间存在线性关系,如果因变量与某个自变量之间呈现出曲线趋势,此时转换的变量可以是自变量,也可以是因变量,或者两者均可。如果进行了变量变换,则应当重新绘制散点图,以保证线性趋势在变换后仍然存在。
(四)关于变量的解释
在对线性回归模型进行解释时,如果使用函数转换的方法对变量进行了转换,则应以转换后的变量给予解释,或者可以根据转换时使用的函数关系,倒推原始自变量对原始因变量的效应大小。基于正态得分法得到的数据,在编秩过程中额外地加入原本不属于数据本身的分布特征,因此并不能直接当做正态数据使用,其标准差、方差等信息与原始数据的计算结果也并不一样;这种转换,仅能用作在构建复杂模型时的探索。