嵌套设计(Nested design)又称巢式设计、窝设计或系统分组设计。当考虑的因素之间存在层次结构时,常采用此设计方案。本文将实例演示在SPSS软件中通过一般线性模型实现嵌套设计资料的方差分析的操作步骤。
关键词:SPSS; 嵌套设计; 巢式设计; 窝设计; 系统分组设计; 一般线性模型; 方差分析
一、案例介绍
研究A、B、C3种催化剂(catalyst:1=A,2=B,3=C)在不同温度(temp:1=低,2=中,3=高)下对某化合物的转化作用[用转化率rate (%)表示]。将催化剂作为一级试验因素,温度作为二级试验因素,采用嵌套设计,每个处理重复两次(order),试验设计及结果见表1。试做方差分析,数据见图1,本案例数据可从“附件下载”处下载。


二、问题分析
本案例是嵌套设计的方差分析,可以按照多因素方差分析进行数据分析,应满足5个条件:
条件1:观察变量唯一,且为连续变量。本研究中观察变量只有转化率,为连续变量,该条件满足。
条件2:有多个因素,且都为分类变量。本研究中有2个因素,都为多水平的分类变量,该条件满足。
条件3:观测值相互独立。本研究中各研究对象的观测值是独立的,不存在互相干扰的情况,该条件满足。
条件4:各组、各水平观测值为正态(或近似正态)分布。
条件5:观察变量不存在显著的异常值。
嵌套设计非完全随机分组,因此不做方差齐性检验。
三、软件操作及结果解读
(一) 适用条件判断
嵌套设计中对异常值的判断一般根据专业知识确定,对正态性一般不做严格要求。如果要进行正态性检验,可参考拉丁方设计(Latin Square Design)资料的方差分析—SPSS软件实现。
(二) 一般线性模型分析过程
选择“分析”—“一般线性模型”—“单变量” (图2)。
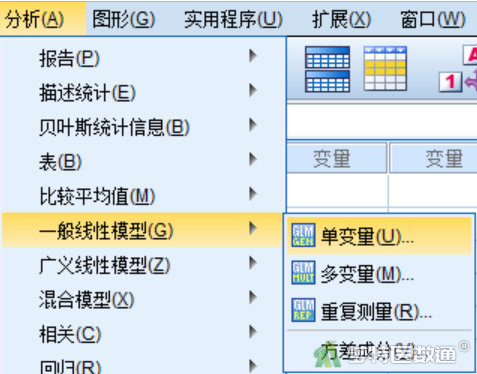
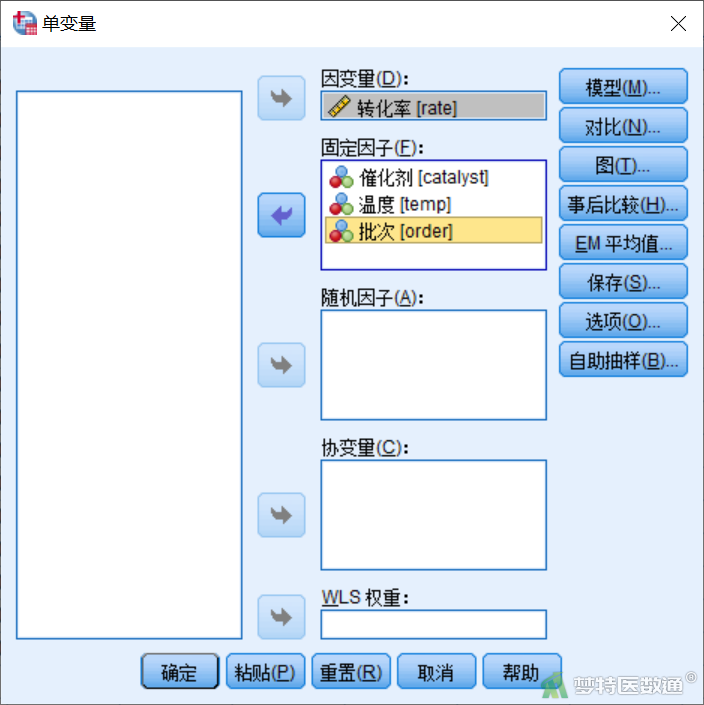
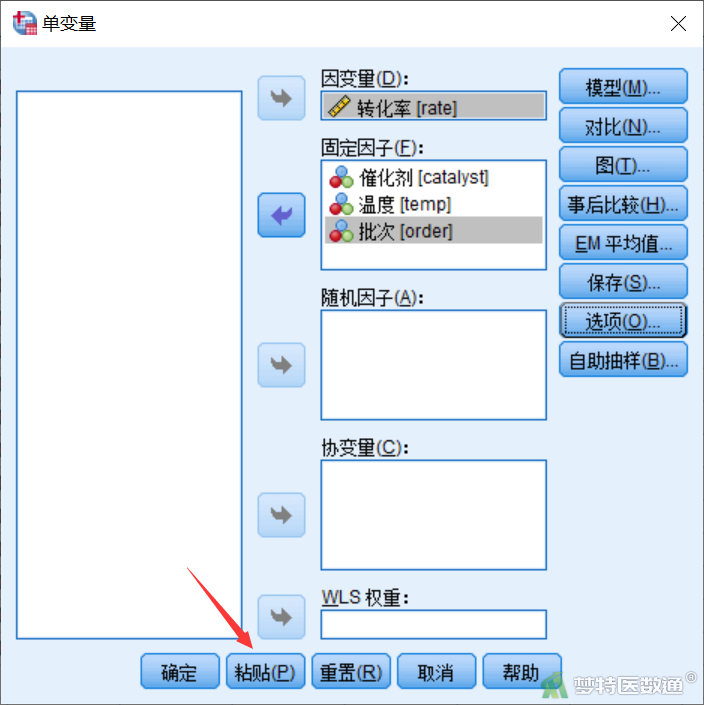
在“单变量”对话框(图3)中,将rate选入右侧“因变量”,将catalyst、temp、order选入右侧“固定因子”。
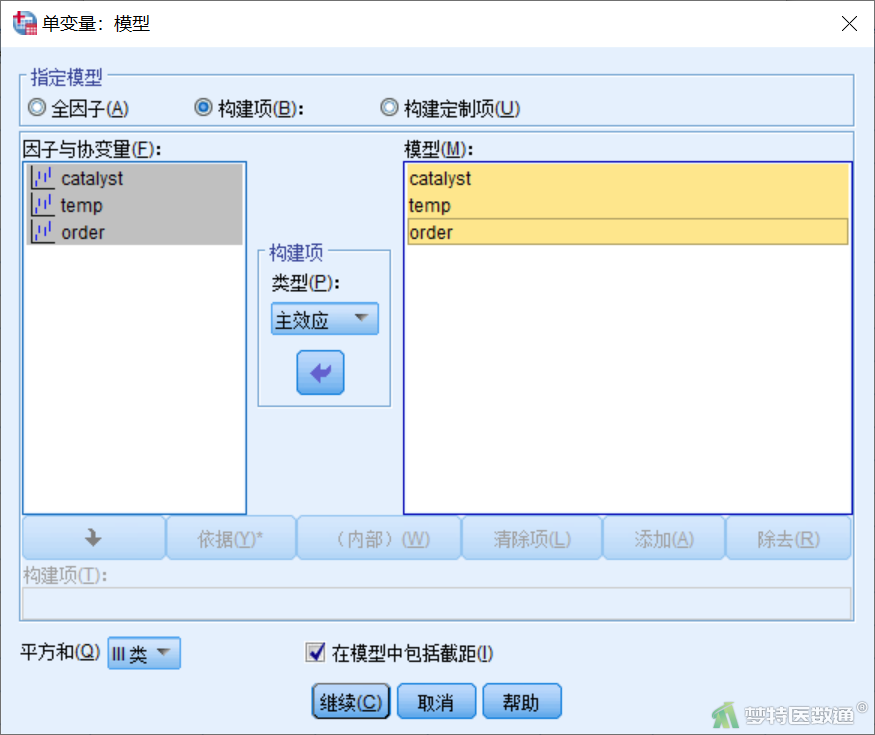
点击图3右侧“模型”,进入“模型”子对话框(图4),点击“构建项”,将catalyst、temp、order的主效应选入右侧“模型”。
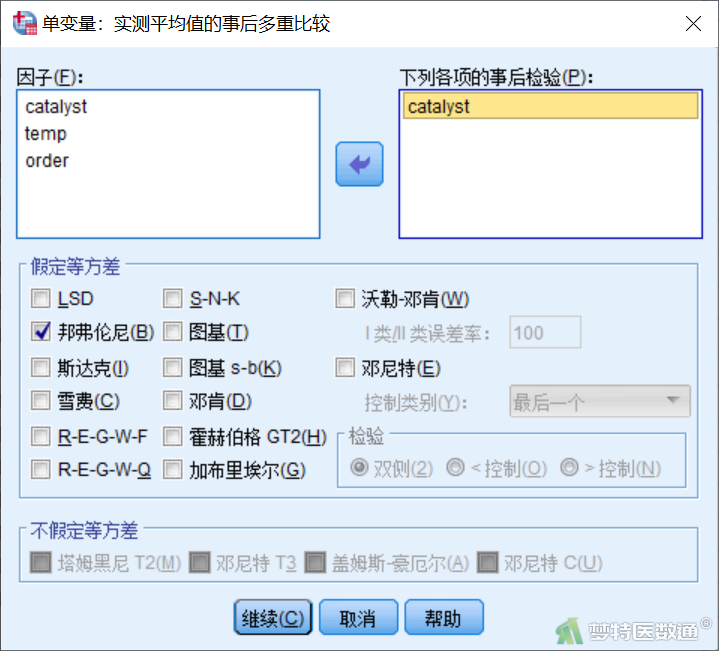
点击图3右侧“事后比较”,进入“实测平均值的事后多重比较”子对话框(图5),将catalyst选入右侧“下列各项的事后检验”,勾选“邦弗伦尼”。
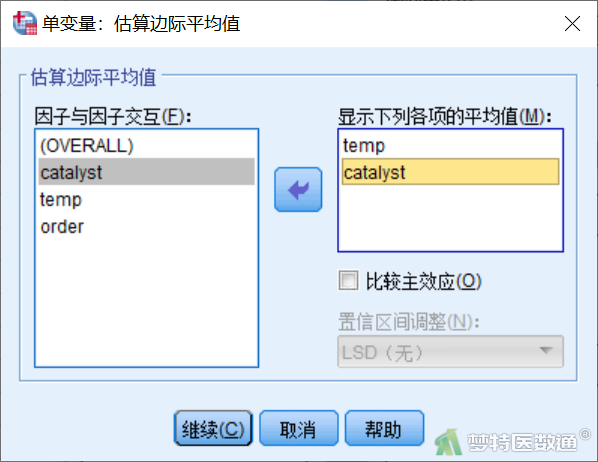
点击图3右侧“EM平均值”,进入“估算边际平均值”子对话框(图6),将temp、catalyst选入右侧“显示下列各项的均值”。
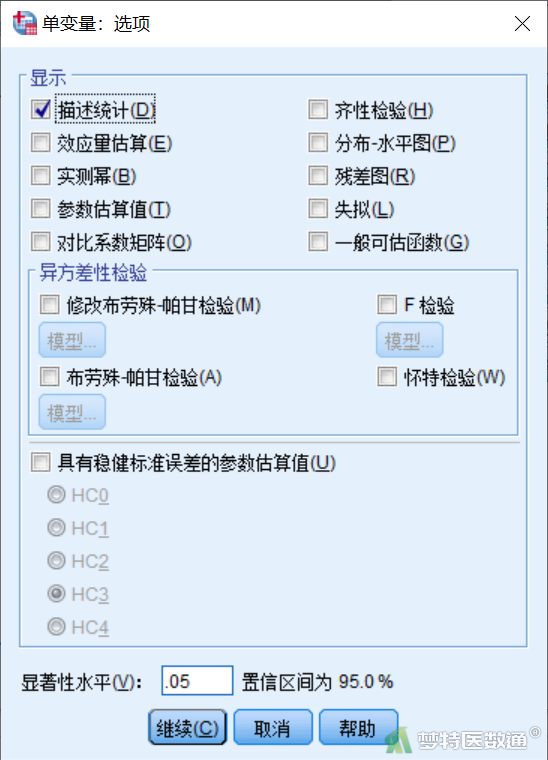
点击图3右侧“选项”,进入“选项”子对话框(图7),勾选“描述统计”。
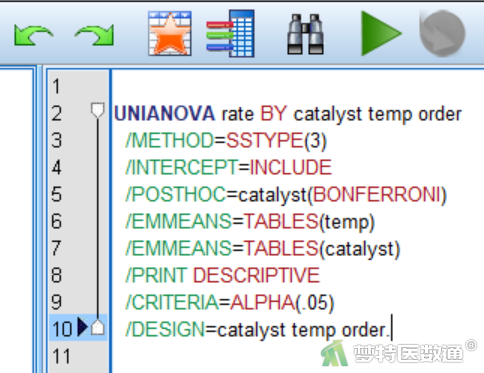
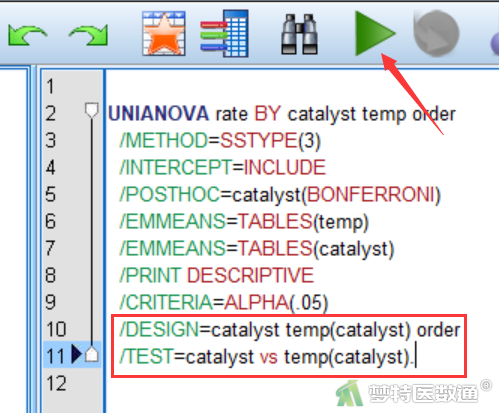
点击图3下方“粘贴”(图8),生成相应程序(图9),将程序更改为图10所示。该程序中“/DESIGN= catalyst temp order”更改为所需的嵌套模型“/DESIGN=catalyst temp(catalyst) order”,并且增加自定义检验“/TEST=catalyst vs temp(catalyst)”。
(三) 结果解读
1. 统计描述/估算边际平均值
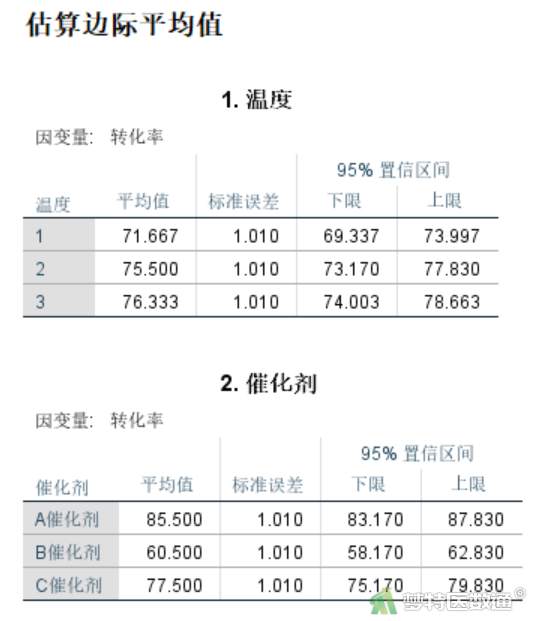
“估算边际平均值”结果见图11,其列出了不同温度和不同催化剂实验条件下的转化率均值和95%置信区间。
2. 方差分析
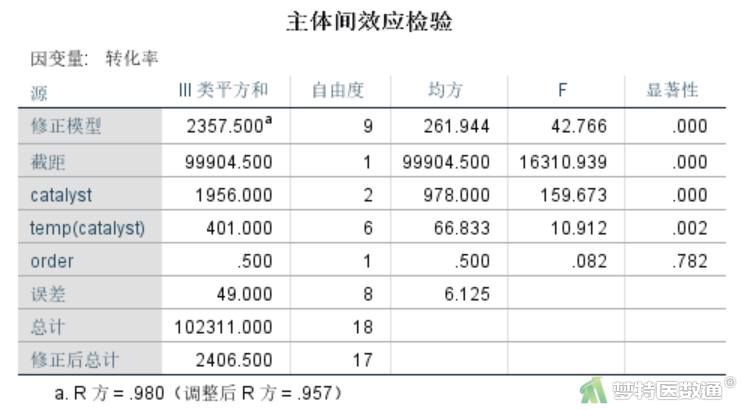
“主体间效应检验”结果(图12)提示,同一催化剂不同温度间的转化率比较,差异有统计学意义(F=10.912,P=0.002)。
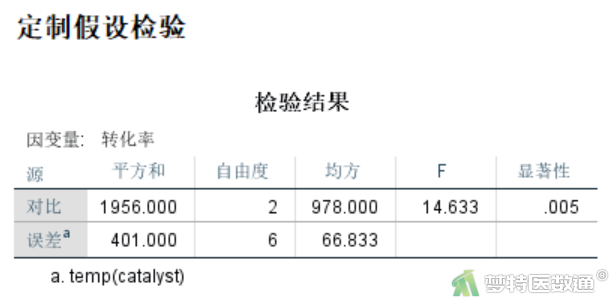
不同催化剂间转化率比较,需以“定制假设检验”结果(图13)为准,结果显示F=14.633,P=0.005,可认为不同催化剂的转化率比较,差异有统计学意义。
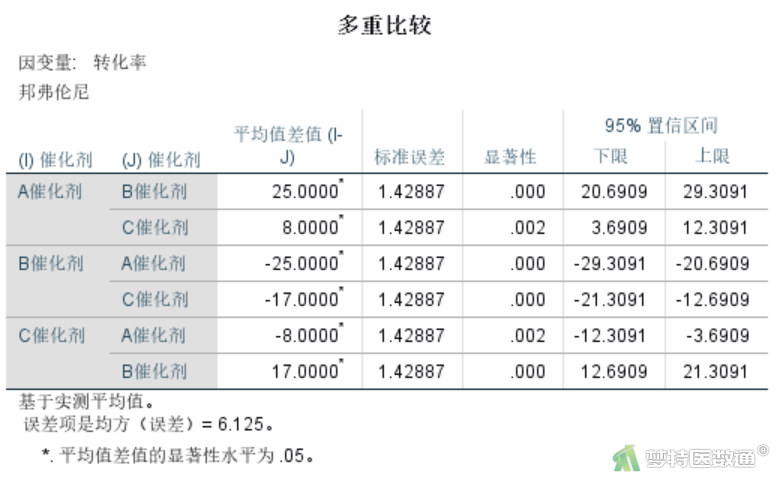
3. 多重比较
多重比较结果见图14,结果显示3组间转化率比较,差异均有统计学意义(P<0.01)。结合图11可知,A催化剂的转化率最高[85.50% (95%CI 83.17%~87.83%)],C催化剂其次[77.50% (95%CI 75.17%~79.83%)],B催化剂最低[60.50% (95%CI 58.17%~62.83%)]。
四、结论
本研究采用嵌套设计研究A、B、C3种催化剂在不同温度下对某化合物的转化作用。分析结果显示,同一催化剂不同温度间的转化率比较,差异有统计学意义(F=10.912,P=0.002)。不同催化剂的转化率比较,差异也有统计学意义(F=14.633,P=0.005)。Bonferroni多重比较发现,3组间差异均有统计学意义(P<0.01)。A催化剂的转化率最高[85.50% (95%CI 83.17%~87.83%)],C催化剂其次[77.50% (95%CI 75.17%~79.83%)],B催化剂最低[60.50% (95%CI 58.17%~62.83%)]。