在前面文章中介绍了一般对数线性模型(General Log-linear Model)在SPSS软件中的操作、原始数据的Logit对数线性模型(Logit Log-linear Model)在SPSS软件中的操作,本文将实例演示在SPSS软件中利用加权数据实现分层对数线性模型(Hierarchical Log-linear Model)的操作步骤。
关键词:SPSS; 分层对数线性模型; 对数线性模型的自动筛选
一般对数线性模型可以对每个系数及总模型给出非常丰富的和详细的信息,但它要求研究者已经有了一定的思路或线索,或只对某些特定效应项感兴趣,即已经有关于简约模型的假设。如果在探索性分析中,研究人员只是假设若干分类变量之间可能有关系,但是并无明确假设,也没有具体分出哪个是因变量,哪个是自变量。此时比较适宜采用分层对数线性模型进行分析(尤其是自变量比较多时),自动筛选无意义的交互项。在SPSS软件中,通过自动筛选(模型选择对数线性分析)实现分层对数线性模型的构建。需要注意的是,分层对数线性模型只提供饱和模型的参数估计,不能输出简约模型的参数估计。在用它得到最佳简约模型后,还应当采用一般对数线性模型来得到具体的参数估计值和检验结果。
一、案例介绍
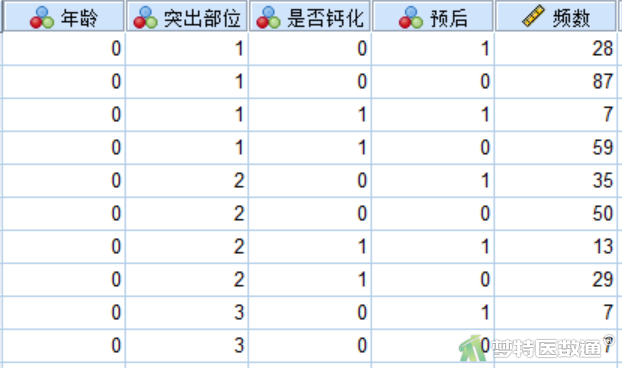
此处仍然采用二分类logistic回归分析(Binomial Logistic Regression Analysis)——SPSS软件实现一文中的案例。探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素,纳入146例治疗效果“不佳”(记录为1)的患者,278例治疗效果“良好”(记录为0)的患者,并统计年龄(0=60岁以下,1=60岁及以上)、突出部位(1=单侧,2=中央,3=极外侧)、是否钙化(0=未钙化,1=钙化)患者的例数。
在一般对数线性模型中,探讨“年龄”和“突出部位”与治疗效果不佳之间是否有关时,使用多因素一般对数线性模型,可手动设置去除“预后*年龄*突出部位”三阶交互作用,保留所有二阶交互作用。在本文中尝试探讨“年龄”“突出部位”“是否钙化”与“预后”之间的关系。相关变量整理为加权数据,部分数据见图1。本案例数据可从“附件下载”处下载。
二、案例分析
由于本案例中存在“年龄”“突出部位”、“是否钙化”“预后”4个变量,如果手动筛选最佳简约模型,太过复杂。此时可通过分层对数线性模型进行自动筛选,得到最佳简约模型。
三、模型筛选
(一) 数据加权
先对数据进行加权。选择“数据”—“个案加权”(图2)。
在“个案加权”页面,将“频数”选入“个案加权依据”下的“频率变量”,单击“确定”(图3)。
(二) 软件操作
选择“分析”—“对数线性”—“选择模型”(图4)。
“因子”中选入“预后”“年龄”“突出部位”“是否钙化”,对每个变量定义范围(图5)。模型构建选择“使用向后去除(U)”,“最大步骤数(A)”和“除去概率(P)”都保持默认数字。
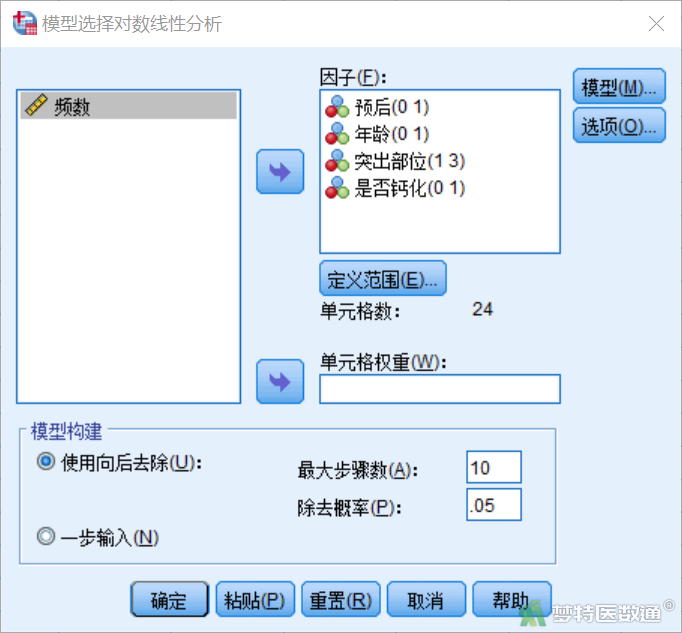
“模型”选项保持默认,即“饱和”模型(图6)。

点击“选项”,勾选“频率”“残差”“参数估算值”“关联表”。将“Delta”中的“0.5”更改为“0”(图7)。
模型在计算时会首先对所有单元格中频数均加上“Delta”值,以避免某些单元格中频数为0时可能引起的计算问题。这样做不会影响统计检验的结果,但是当数据量较少时会略微影响参数的估计值。因此,数据较为简单时,若不存在空单元格,则建议将“Delta”设定为0;若存在空单元格,则将“Delta”设定为0.5。
(三) 结果解读
图8中“数据信息”列出了案例数和变量的水平数;“收敛信息”呈现了迭代收敛信息。

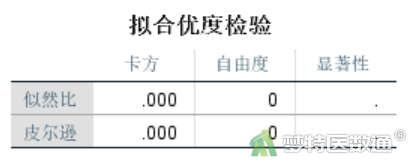
由于此时拟合的是饱和模型,因此“拟合优度检验”表格(图9)为空。
“K向效应和更高阶效应”结果(图10)所示的是检验模型中k维交互作用及k维以上交互作用是否有统计学意义,即k维交互作用自身是否有统计学意义,方法为似然比卡方或皮尔森逊卡方,可见无论哪种检验均显示4维和3维交互作用无统计学意义,但二维交互和主效应均有统计学意义。
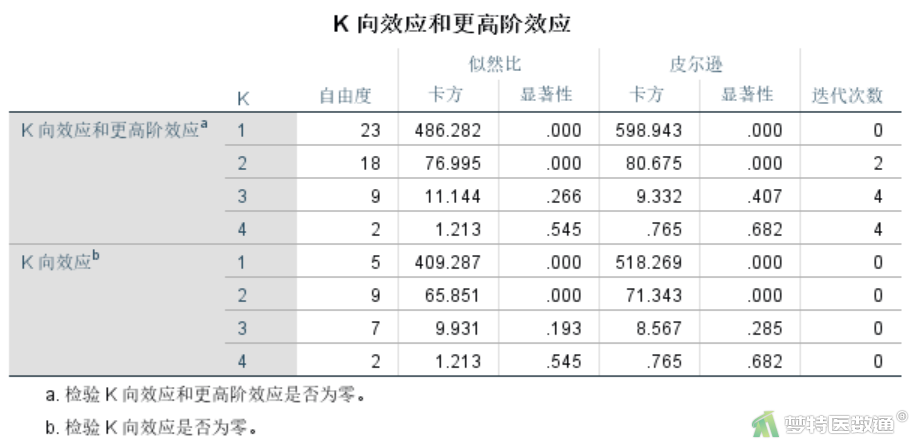
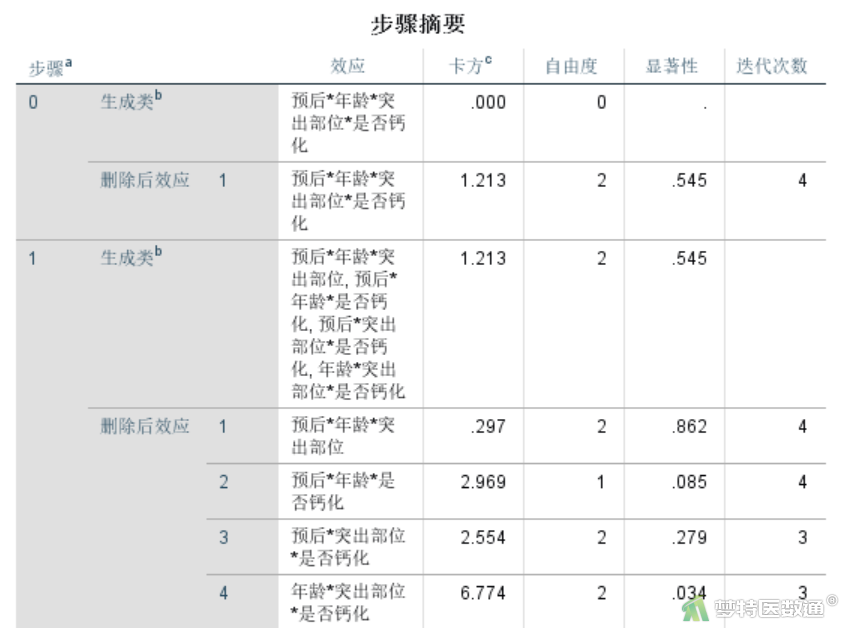
图11-1~图11-2“步骤摘要”结果显示的是,数据从高级别的交互项向低级别的交互项逐步计算的过程。
第0步为初始模型,首先是初始模型的拟合优度检验(表示方法是显示最高阶交互作用),与上面的分析结果一样,卡方值为零。随后给出去除模型中最高阶交互作用项后拟合优度的改变有无统计学意义的结果。可见P=0.545,显然去除四阶交互作用项对模型无影响。
在第一步中,四阶交互作用项已被去除,当前模型中的最高阶交互作用项为4个三阶交互作用项,右侧的检验为当前模型拟合优度与饱和模型相比的检验,可见无统计学差异(P=0.545)。随后分别计算如果将这几个最高阶交互作用项从模型中去除,拟合优度的改变有无统计学意义。可见,可以考虑去除“预后*年龄*突出部位”(P=0.862)、“预后*年龄*是否钙化”(P=0.085)、“预后*突出部位*是否钙化”(P=0.279),但“年龄*突出部位*是否钙化”(P=0.034)三阶交互作用项则需要保留。
依次类推,可以解读每一步骤中需要剔除的模型项和需要保留的模型项。第8步最后模型中保留的交互项为“预后*突出部位”“预后*年龄”“预后*是否钙化”“年龄*是否钙化”。
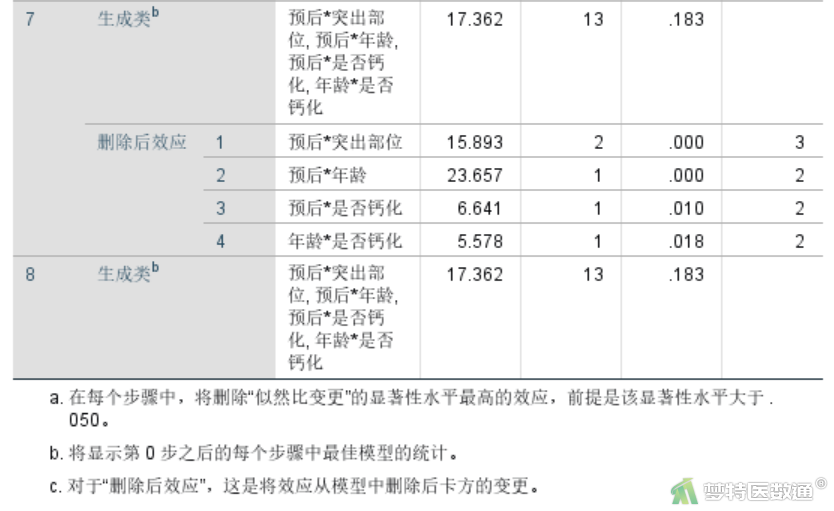
“收敛信息”结果(图12)给出的是最终模型的信息,同样是用列出模型中具体系数的方式来表示。可见,本研究应纳入“预后*突出部位”“预后*年龄”“预后*是否钙化”“年龄*是否钙化”4个交互项,并包含涉及交互项的主变量“预后”“年龄”“突出部位”“是否钙化”。

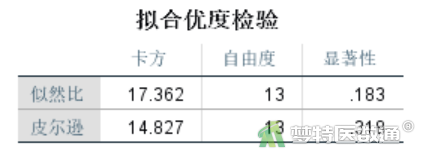
“拟合优度检验”结果(图13)可见模型拟合良好。现在已经得到了最佳简约模型,但上面的分析中并未给出各项的系数以及各项的详细检验结果,因此,还应当采用一般对数线性模型来得到具体的参数估计值和检验结果。
四、一般对数线性模型
(一) 软件操作
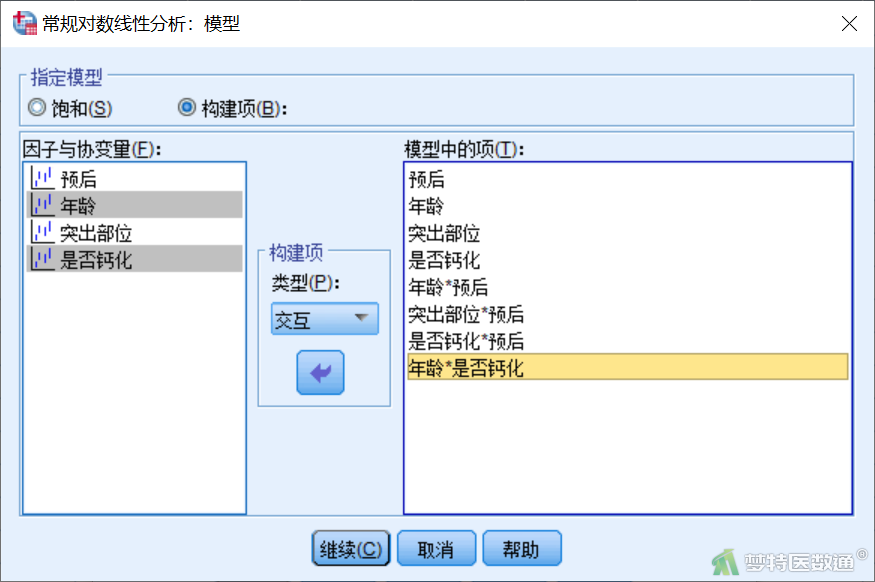
具体操作详见一般对数线性模型分析,此处只是在“模型”选项中,需要使用“构建项”,并将“预后”“年龄”“突出部位”“是否钙化”“预后*突出部位”“预后*年龄”“预后*是否钙化”“年龄*是否钙化”依次(先选择主效应,再选择二阶交互作用项)选入右侧模型(图14)。
(二) 结果解释
“拟合优度检验”结果(图15)同时输出似然比检验(likelihood ratio)和Pearson卡方检验(Pearson chi-square test)的模型拟合结果。当样本量比较大的时候,这两个检验的结果基本一致。但如果样本量小,似然比检验和Pearson卡方检验的结果会出现比较大的差异,这时推荐根据似然比检验判断模型拟合程度。
一般来说,如果数据预测频数接近观测频数,模型的拟合程度就比较好,检验结果将提示卡方值比较小,P值较大。即当检验结果P>0.05时,提示模型拟合好,结果准确性强。但如果检验结果P<0.05,就说明模型拟合程度不好,提示应适当调整模型,重新进行模型筛选。
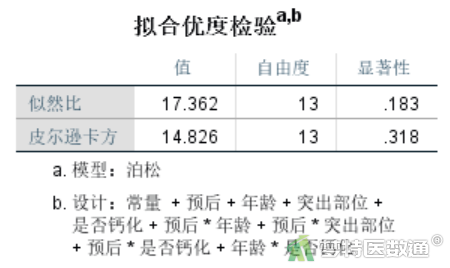
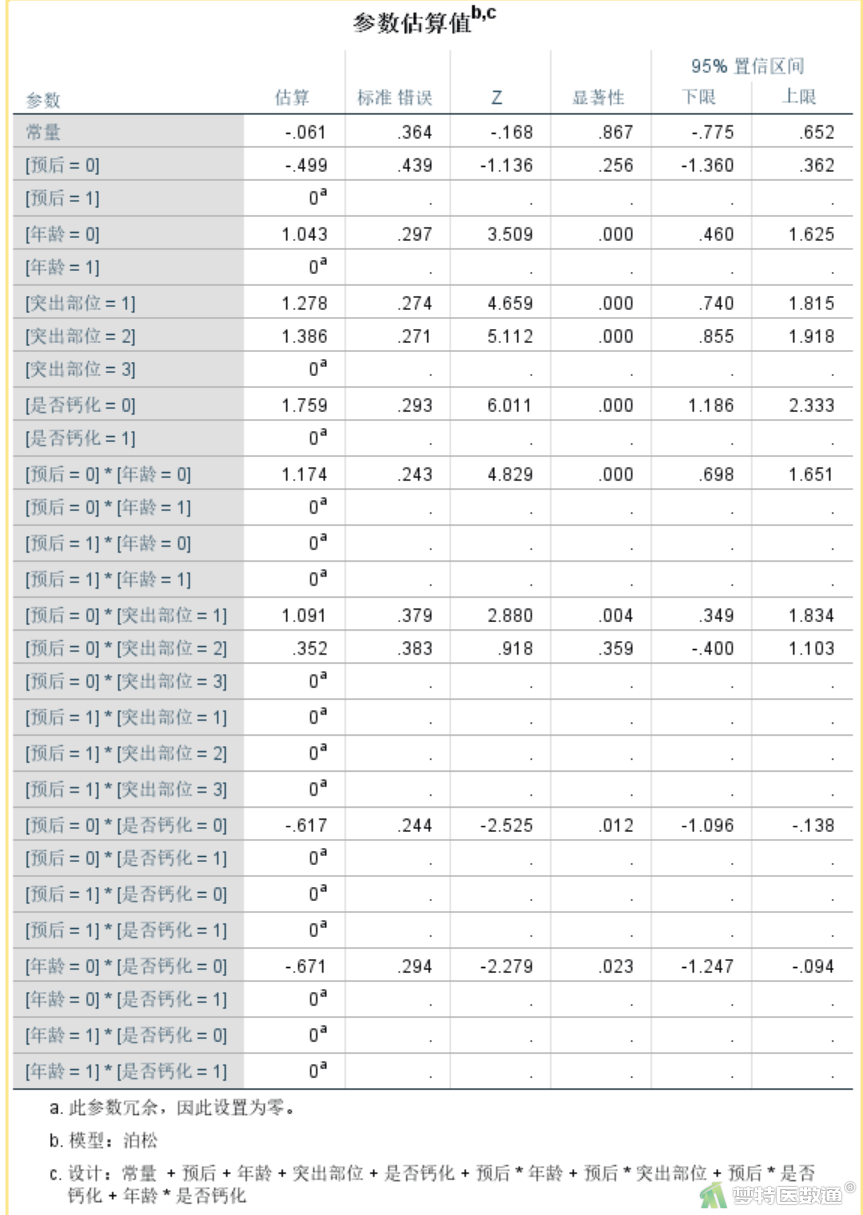
“参数估算值”结果(图16)中,“预后”和“年龄”之间的交互作用项有统计学意义(P<0.001),OR=Exp(1.174) = 3.234906,即常数e的1.174次方。根据已有因果关联专业知识,可认为“60岁以下”者预后良好的概率约为“60岁及以上”者的3.234906倍,即“60岁及以上”者预后不佳的风险约为“60岁以下”者的3.234906倍。同理,可知“单侧”患者预后良好的概率是“极外侧”患者的2.565107倍(P=0.018),“中央”患者预后良好的概率是“极外侧”患者的1.130884倍(P=0.760)。“非钙化”患者术后不佳的风险是“钙化”患者的1.85336倍(OR=1/(exp(-0.617));P=0.012)。
五、结论
本研究采用对数线性模型进行自动筛选最佳简约模型,根据后退剔除法,最终模型包含“预后”“年龄”“突出部位”“是否钙化”4个主变量和“预后*突出部位”“预后*年龄”“预后*是否钙化”“年龄*是否钙化”4个交互项。似然比检验结果显示χ2=17.362,P=0.183,说明模型拟合程度较好。系数结果提示“年龄”、“突出部位”“是否钙化”均与“预后”有关。根据已有因果关联专业知识,可认为“60岁以下”者预后良好的概率约为“60岁及以上”者的3.234906倍;“单侧”患者预后良好的概率是“极外侧”患者的2.565107倍(P=0.018),“中央”患者预后良好的概率是“极外侧”患者的1.130884倍(P=0.760);“非钙化”患者术后不佳的风险是“钙化”患者的1.85336倍(P=0.012)。
六、分析小技巧
- 对数线性模型为层次模型,如果模型中包含了某几个变量的高级交互效应时,这几个变量的低阶交互效应项与主效应也一定包含在模型中。一旦一个低阶交互效应为0,相应的其他高阶交互效应全部为0。
- 对数线性模型的建立一般以饱和模型开始,饱和模型包含了所有变量的主效应、低阶交互效应和高阶交互效应。通过后退法逐渐排除没有统计学意义的作用项,最后拟合最优的简化模型及不饱和模型。对数线性模型在分析过程中主要是寻找符合实测样本资料的适当模型。所谓“适当”的模型不仅是指模型成立,而且要求模型尽量简单,不含无意义的高阶交互作用。
- 对数线性模型的局限性:(1)模型的解释:对数线性模型中较多的变量经常使得模型的解释较为困难。(2)对数线性模型中没有明确定义的自变量和因变量,但在实际应用中,由于变量的实际意义,导致有自变量和因变量之分。(3)对数线性模型只能分析分类变量之间的联系,当分析变量之间具有明确的自变量、因变量之分,或者获得的连续性变量不能转化为分类变量时,需要考虑logistic回归模型。