对数线性模型是分析分类变量的重要模型,多用于列联表资料。该模型和卡方检验、方差分析模型、Logistic回归模型之间均存在密切关联。
关键词:SPSS; 对数线性模型; 列联表; 卡方检验; 方差分析模型; Logistic回归模型
一、对数线性模型与方差分析模型的关系
对数线性模型的构造类似于方差分析模型,其作用也与方差分析类似,能分析各变量的主效应及变量间的交互效应。但对数线性模型与方差分析模型也存在明显区别。首先体现在方差分析的因变量是连续变量,对其分布有特定要求,如需要满足正态性和方差齐性,旨在研究不同因素对该连续变量的影响。而对数线性模型主要研究多个分类变量间的统计独立与依赖性。一般而言,对数线性模型的特点是对所有的变量不分因变量和自变量一视同仁的分析。模型中分析的是各因素对单元格中频数的影响,通常假设单元格中频数服从多项式分布。另一个区别在于,方差分析中各因素对因变量的作用是相加的,而对数线性模型中各因素对单元格中频数的作用则是相乘的。
二、对数线性模型与卡方检验的关系
对数线性模型是列联表资料分析方法的拓展。应用于二维及多维列联表资料的分析,主要考察各分类变量间的交互作用(关联性)。卡方检验仅用于二维列联表资料的分析,不能分析二维以上列联表中变量的关系。对数线性模型是分析高维列联表的一种非常有效的方法,它可以通过分析交互项效应来挖掘多个分类变量间的深层关系。利用对数线性模型对列联表资料进行分析时,不区分因变量和自变量。他强调的是模型的拟合,优度检验和分类变量间交互效应的检验。
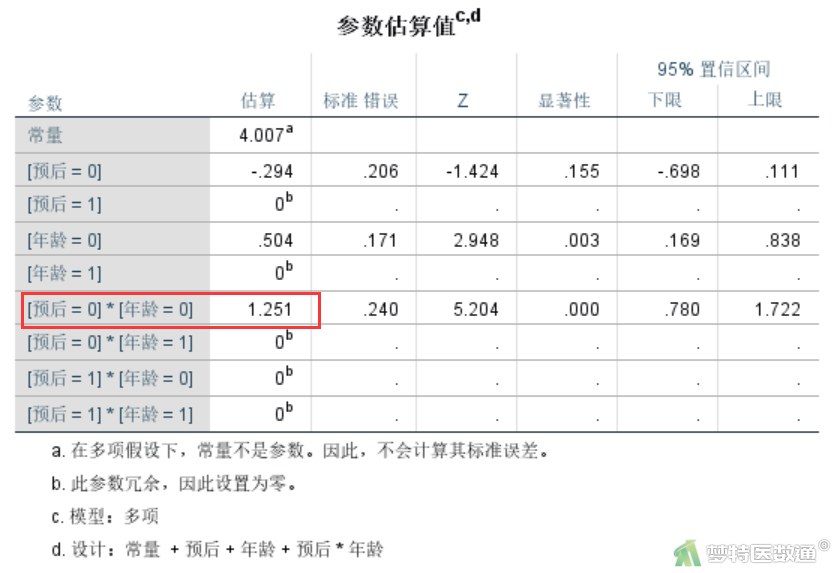
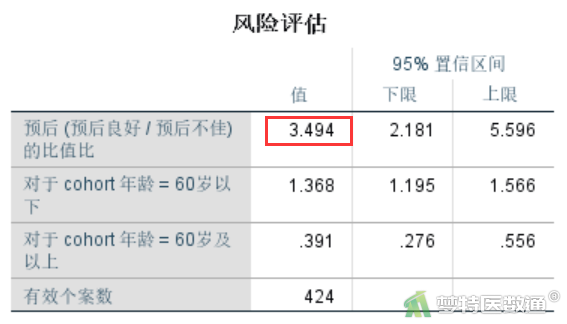
对于二维列联表资料,对数线性模型与卡方检验完全等价。如基于原始数据的一般对数线性模型(General Log-linear Model)——SPSS软件实现一文中,“预后”和“年龄”的交互作用具有统计学意义(P<0.001),OR年龄=Exp(1.251)=3.493835(图1)。通过卡方检验计算其OR值为3.494,P<0.001(图2),和对数线性模型完全一致。
三、对数线性模型与Logistic回归模型的关系
(一) 对数线性模型与Logistic回归模型的联系
对数线性模型主要研究多个分类变量间的统计独立与依赖性。而logistic回归的因变量是分类变量,研究多个自变量与分类变量之间的关系。因此对数线性模型与logistic回归两种方法之间存在着非常密切的联系,只需要在对数线性模型中将单元格中频数的理论分布改为Logit,则对数线性模型的Logit过程和Logistic回归的结果就完全等价。
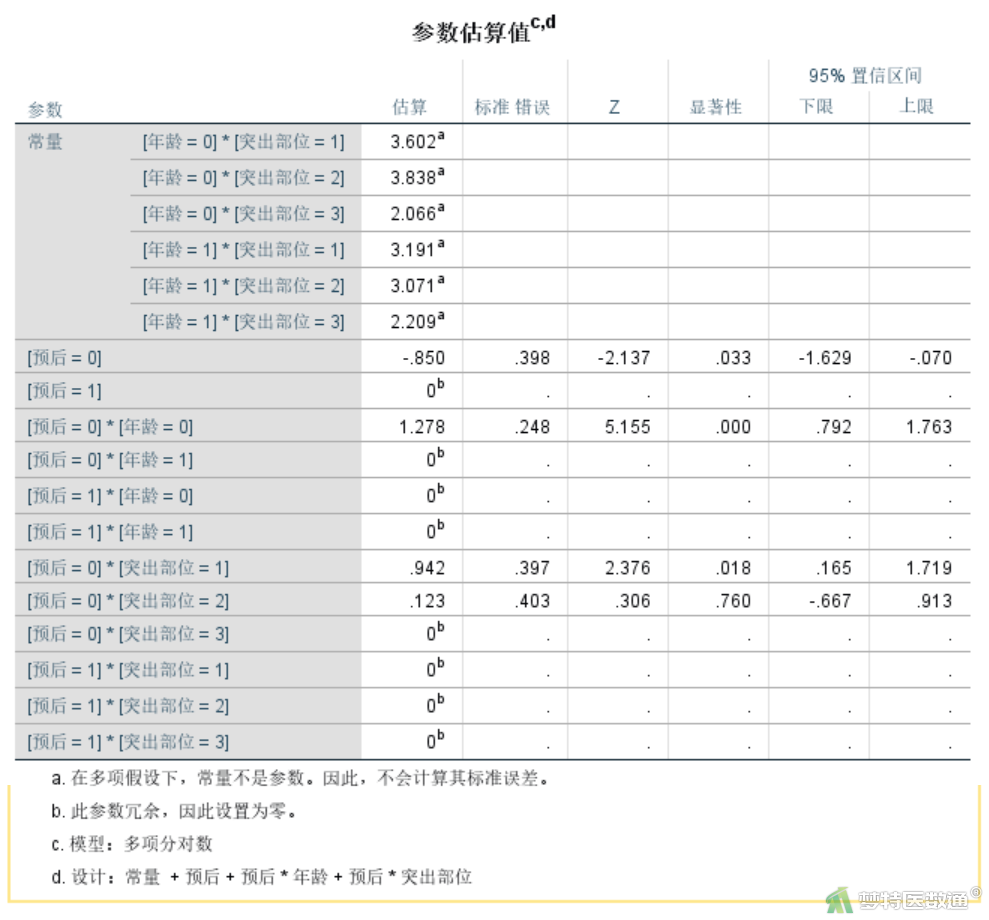
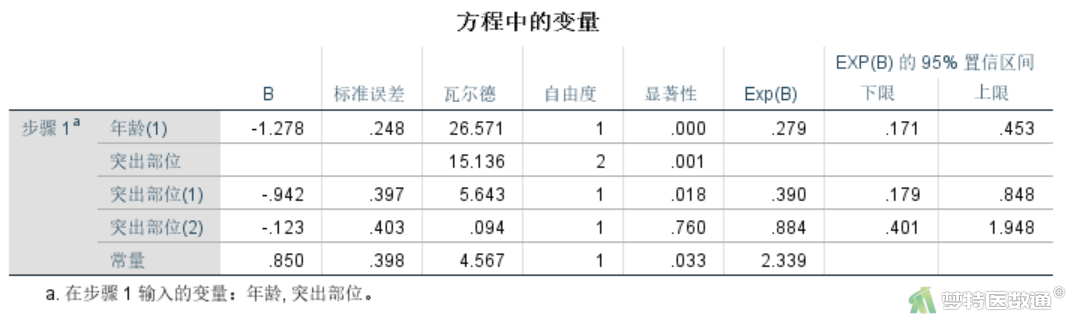
可以实例证明包括所有主效应和与主效应相关的二阶交互作用的Logit对数线性模型完全等价于Logistic回归模型(注意:层次对数线性模型得到的最优简化模型并不一定等价于Logistic回归模型)。如在基于原始数据的Logit对数线性模型(Logit Log-linear Model)——SPSS软件实现一文中,通过Logit对数线性模型计算得到“预后”和“年龄”的交互作用具有统计学意义(P<0.001),OR年龄=Exp(1.278)= 3.589454;“单侧”患者预后良好的概率是“极外侧”患者的2.565107倍(P=0.018),“中央”患者预后良好的概率是“极外侧”患者的1.130884倍(P=0.760) (图3)。其结果与二分类Logistic回归模型分析结果完全一致(图4)。
(二) 对数线性模型与Logistic回归模型的区别
在实际应用过程中,对数线性模型的应用远不如Logistic回归普遍,其主要原因在于:
- 模型的解释较为复杂:对数线性模型中当变量较多时,模型会变得非常复杂,使得模型的解释较为困难。尽管SPSS软件在分层对数线性模型中提供了最佳简约模型的选择过程,但是模型的复杂性的确限制了对数线性模型的应用和推广。
- 对数线性模型中没有明确定义的自变量和因变量,但在实际应用中,由于变量的实际意义,导致有自变量和因变量之分。尽管Logit对数线性模型可以解决因果关系明确的模型构建,但正如上所述,在自变量较多时对数线性模型存在着固有的局限性。
- 对数线性模型只能分析分类变量之间的联系,不能分析连续变量存在模型中,当有连续变量时需要将其转化为分类变量。如果不能成功转化为分类变量,则需要考虑Logistic回归模型。
尽管对数线性模型存在一定的缺陷,但模型本身并无优劣之分,只有适用与否。当多个分类变量之间分不出因果关系,或研究者对变量之间的因果关系并不感兴趣,仅需分析变量之间的相互关系时更多使用对数线性模型,而较少使用Logistic回归模型。