在前面文章中介绍了对数线性模型(Log-linear model)的相关理论,SPSS中提供了3个关于对数线性模型的子菜单:常规、分对数和选择模型;这3个子菜单的分析过程都应用对数线性模型的基本原理,但在拟和方法和结果输出上有所不同。本文将实例演示在SPSS软件中实现加权数据构建一般对数线性模型(General Log-linear Model)的操作步骤。
关键词:SPSS; 对数线性模型; 一般对数线性模型; 因果关系不明的对数线性模型
一般对数线性模型用于研究人员只对某些特定效应项感兴趣的情况,属于证实性研究,在分析中只考虑因素之间是否相关,并不考虑彼此之间的因果关系,最后在结果解释时由研究人员作出判断。
一、案例介绍
此处采用二分类logistic回归分析(Binomial Logistic Regression Analysis)——SPSS软件实现一文中的案例。探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素,纳入146例治疗效果“不佳”(记录为1)的患者,278例治疗效果“良好”(记录为0)的患者,并统计年龄(0=60岁以下,1=60岁及以上)、突出部位(1=单侧,2=中央,3=极外侧)患者的例数。部分数据见图1。本案例数据可从“附件下载”处下载。
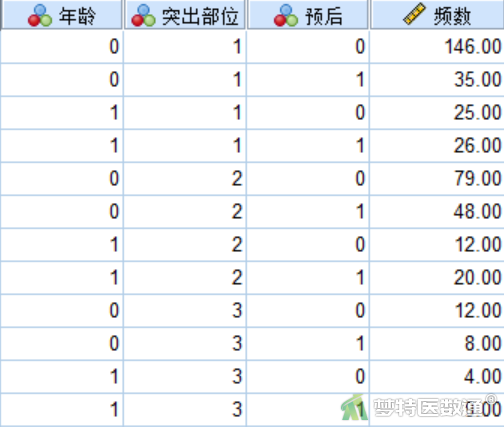
二、案例分析
本案例的分析目的是探讨“年龄”和“突出部位”与治疗效果不佳之间是否有关,由于因变量是二分类变量、自变量是二分类或多分类变量,因此在单因素分析时可以使用卡方检验或二分类logistic回归分析,在多因素分析时可以使用二分类logistic回归分析。此处也可以使用对数线性模型,假设不区分因果关系,可以使用一般对数线性模型进行数据分析。
三、单因素分析
(一) 数据加权
先对数据进行加权。选择“数据”—“个案加权”(图2)。
在“个案加权”页面,将“频数”选入“个案加权依据”下的“频率变量”,单击“确定”(图3)。
(二) “年龄”与“治疗效果不佳”之间的关系
1. 软件操作
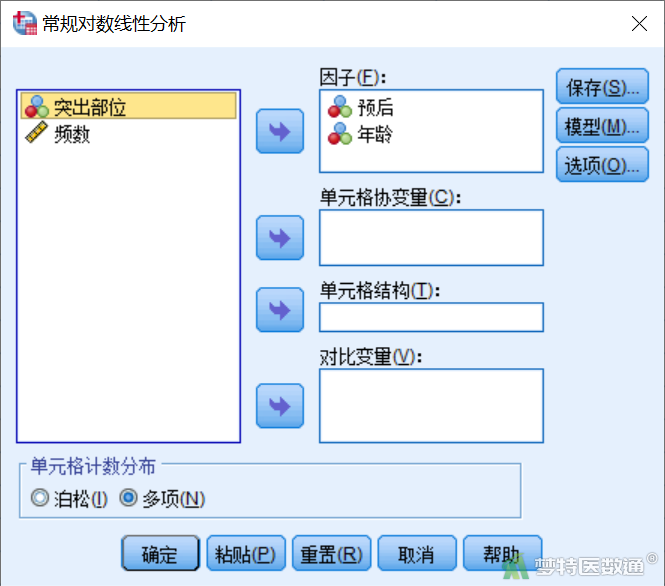
选择“分析”—“对数线性”—“常规”(图4)。

打开“常规对数线性分析”对话框(图3),“因子”中选入需要分析的各个因素;“单元格协变量”中选入模型中需要引入或控制的连续性变量,此时模型在拟合时会对每一个单元格按照该变量的平均水平进行估计;“单元格计数分布”中选择单元格中频数的分布,一般默认为“泊松”分布;主对话框上的另外几个框组都是在拟合“泊松”回归模型时使用的。本例“因子”中选入“预后”和“年龄”,“单元格计数分布”选择“多项”,点击“确定”即可。
“模型”中保持默认,即“饱和”模型(图6)。
点击“选项”,勾选“频率”“残差”“估算值”。将“Delta”中的“0.5”更改为“0”(图7)。
模型在计算时会首先对所有单元格中频数均加上“Delta”值,以避免某些单元格中频数为0时可能引起的计算问题。这样做不会影响统计检验的结果,但是当数据量较少时会略微影响参数的估计值。因此,数据较为简单时,若不存在空单元格,则建议将“Delta”设定为0;若存在空单元格,则将“Delta”设定为0.5。
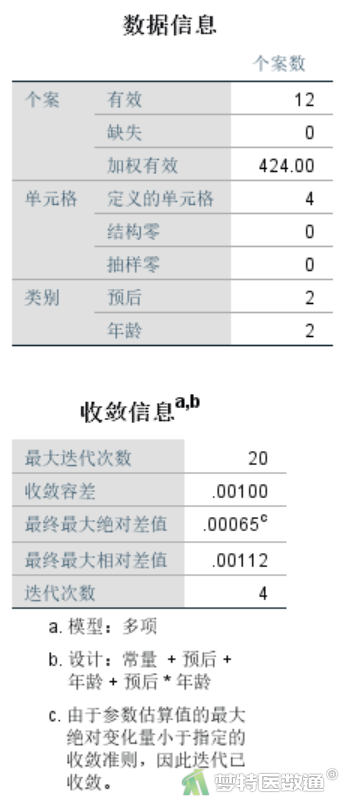
2. 结果解读
图8中“数据信息”列出了案例数和变量的水平数。“收敛信息”呈现了迭代收敛信息。
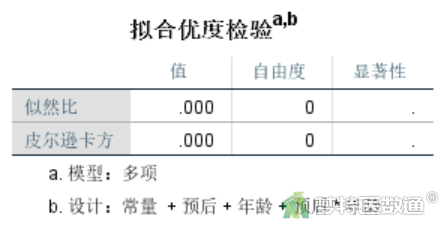
由于此时拟合的是饱和模型,因此“拟合优度检验”表格(图9)为空。
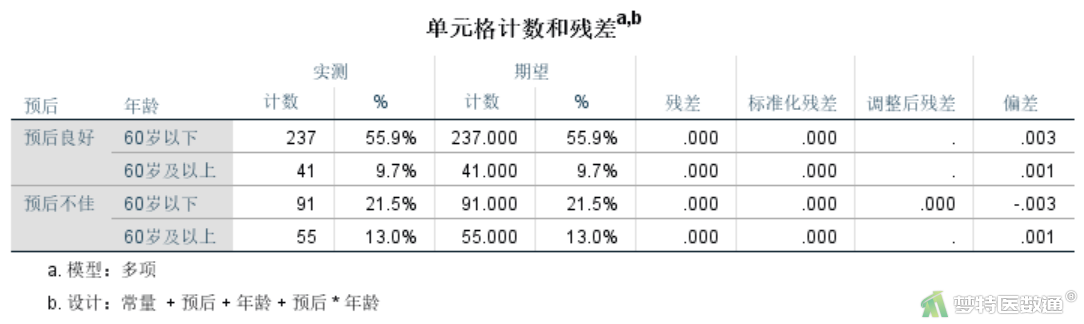
“单元格计数和残差”表格(图10)中所列的为各单元格的实际频数、理论频数及其占总样本例数的比例等。由于拟合的是饱和模型,因此各单元格的实际频数和理论频数完全相同。各单元格拟合的残差、校正残差与偏差均为零0。
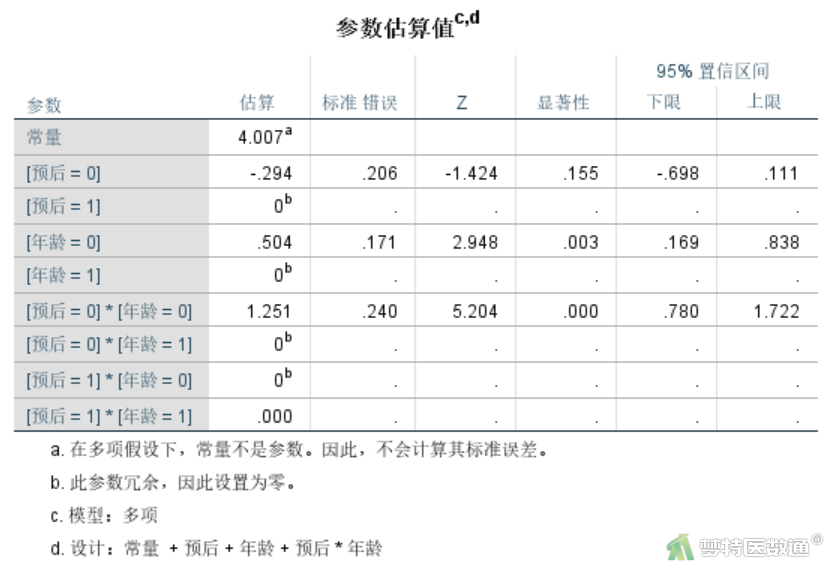
“参数估算值”表格(图11)是对数线性模型的关键结果,模型中列出了各参数的估计值、标准误差、服从标准正态分布的Z值及回归系数的95%置信区间。模型共有9个参数,但真正进入模型的参数只有4个。参数1为常数项,参数2为变量“预后”的主效应项,参数4为变量“年龄”的主效应项,参数6是“预后”和“年龄”的交互作用项。根据研究目的,最关注的是参数6的估计值及假设检验结果,即两个因素的交互作用是否有意义。可见,“预后”和“年龄”的交互作用具有统计学意义(P<0.001),OR年龄=Exp(1.251)=3.493835,即常数e的1.251次方。根据已有因果关联专业知识,可认为“60岁以下”者预后良好的概率约为“60岁及以上”者的3.493835倍,即“60岁及以上”者预后不佳的风险约为“60岁以下”者的3.493835倍。
(三) “突出部位”与“治疗效果不佳”之间的关系
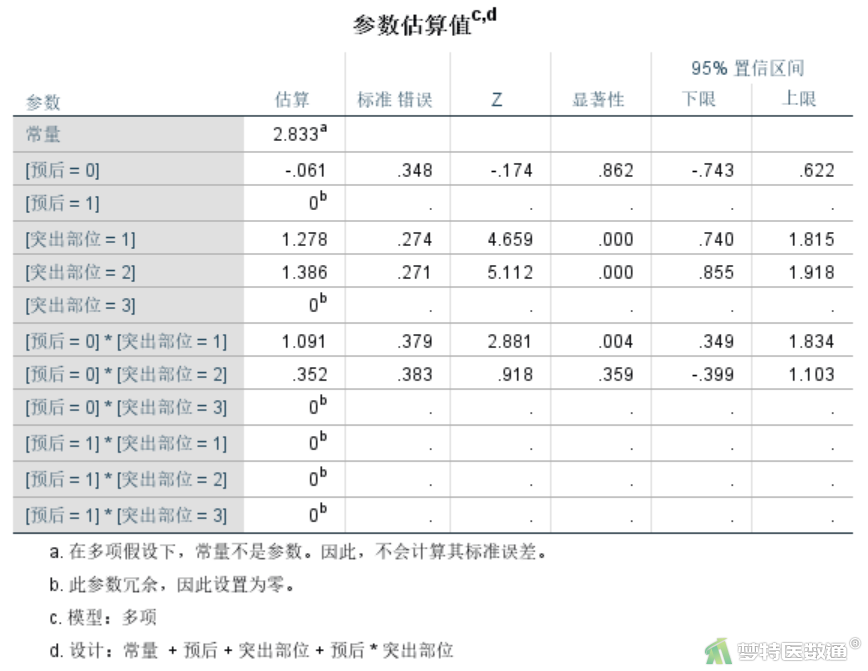
参照上述操作分析“突出部位”与“治疗效果不佳”之间的关系。主要分析结果如图12所示。主要关注“预后”和“突出部位”之间的交互作用是否有统计学意义。
OR单侧=Exp (1.091)= 2.97725,OR中央=Exp (0.352)= 1.421909。根据已有因果关联专业知识,可认为“单侧”患者预后良好的概率是“极外侧”患者的2.97725倍(P=0.004),“中央”患者预后良好的概率是“极外侧”患者的1.421909倍(P=0.359)。
(四) 交互作用检验
单因素分析的目的是检验“年龄”或“突出部位”与“预后”两个变量之间有无交互作用。因此,另一个更简单的分析思路是比较包含交互作用的模型和不包含交互作用的模型之间是否存在统计学差异即可。此处以“年龄”为例,在“模型”中选择“构建项”,将“年龄”和“预后”的主效应选入右侧模型,此时不放入“预后*年龄”交互项(图13)。
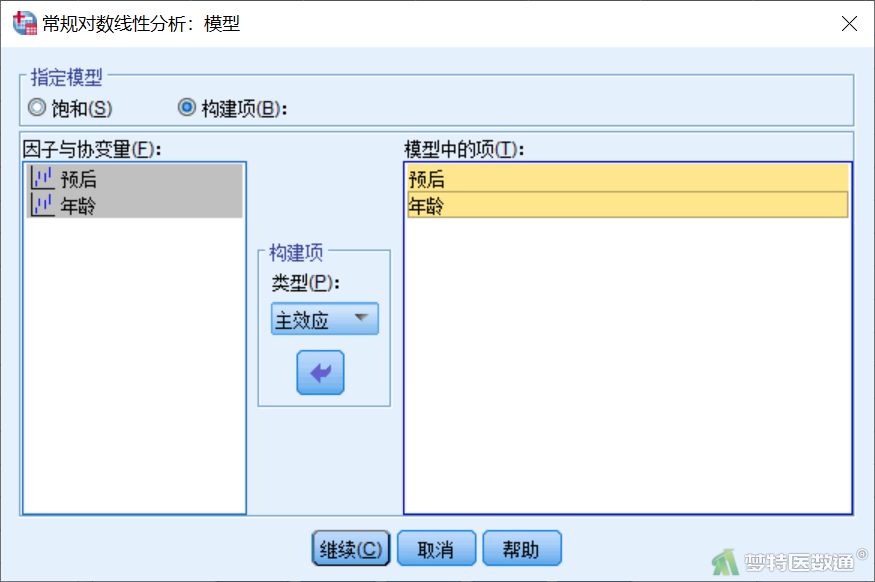
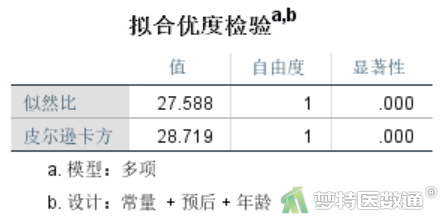
从“拟合优度检验”分析结果(图14)可知,不包含交互作用的模型与饱和模型(包含交互作用)相比,差异有统计学意义,这表明交互作用是具有统计学意义的。
四、多因素分析
多因素分析是研究“年龄”“突出部位”两个变量同时存在时各自与“预后”的关联,那么需要在模型中控制“年龄*突出部位”两个变量之间的交互影响即可。分析操作如图15所示,“年龄”“突出部位”“预后”的主效应必须包含在模型中,“预后*年龄”是为了检验“年龄”对“预后”的影响,“预后*突出部位”是为了检验“突出部位”对“预后”的影响,“年龄*突出部位”是为了检验在控制“年龄”和“突出部位”之间相互影响的情况下,“年龄”和“突出部位”两个变量对“预后”的影响。
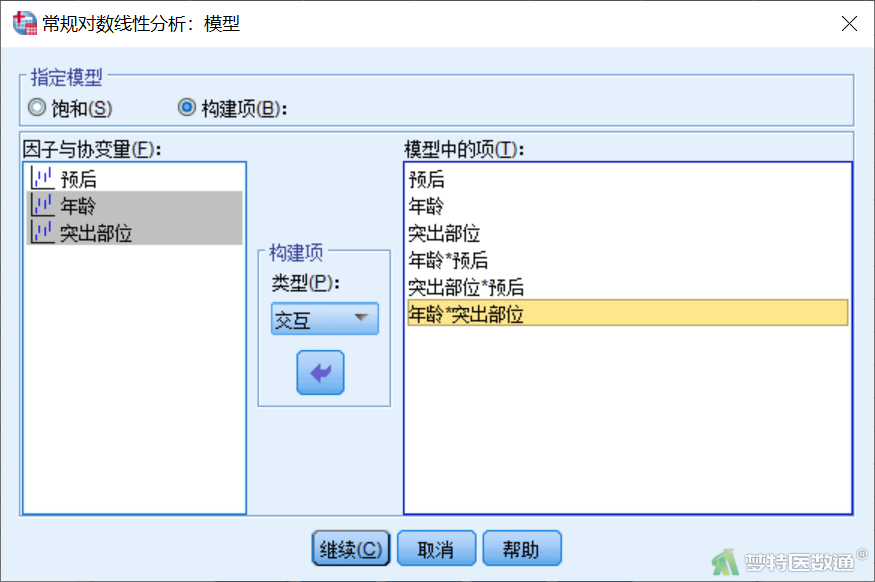
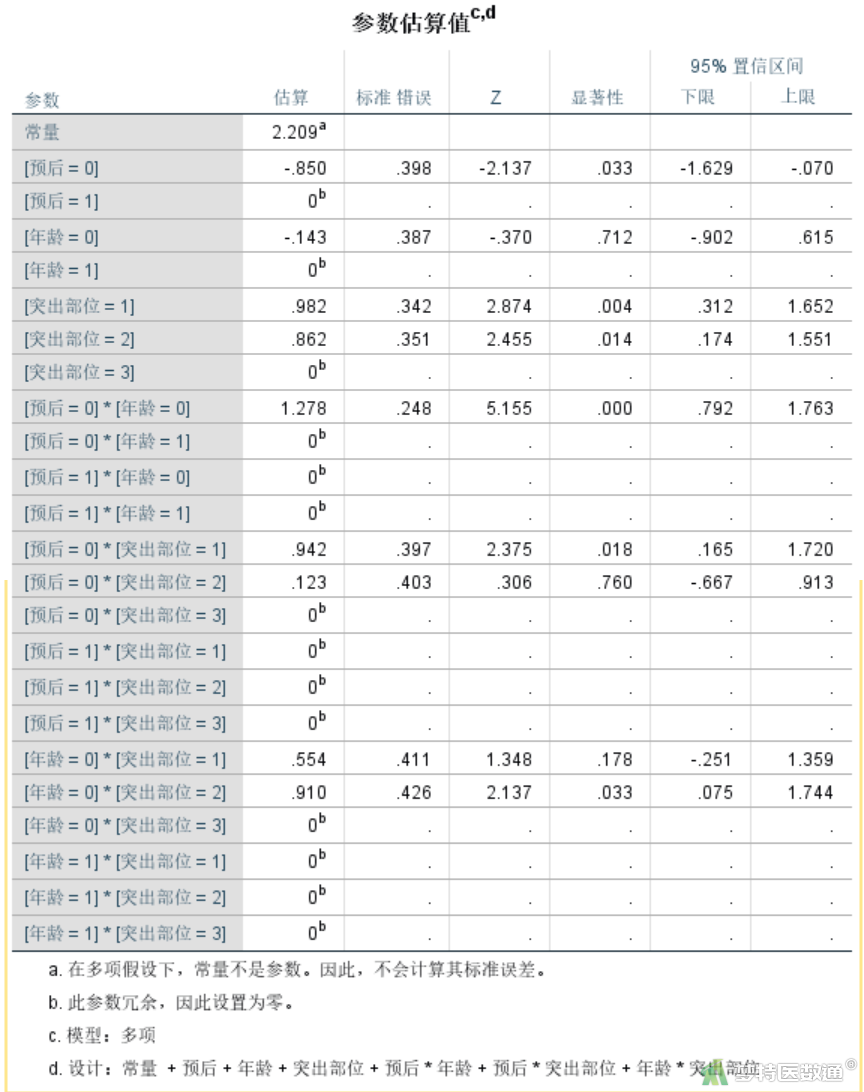
图16是主要分析结果。可知“预后”和“年龄”的交互作用具有统计学意义(P<0.001),OR年龄=Exp(1.278)= 3.589454。根据已有因果关联专业知识,可认为“60岁以下”者预后良好的概率约为“60岁及以上”者的3.589454倍,即“60岁及以上”者预后不佳的风险约为“60岁以下”者的3.589454倍。同理,可知“单侧”患者预后良好的概率是“极外侧”患者的2.565107倍(P=0.018),“中央”患者预后良好的概率是“极外侧”患者的1.130884倍(P=0.760)。
五、结论
“年龄”和“突出部位”均与预后有关。根据已有因果关联专业知识,可认为“60岁以下”者预后良好的概率约为“60岁及以上”者的3.589454倍,“单侧”患者预后良好的概率是“极外侧”患者的2.565107倍(P=0.018),“中央”患者预后良好的概率是“极外侧”患者的1.130884倍(P=0.760)。
六、分析小技巧
使用对数线性模型进行多因素分析,在模型设置时,“构建项”中如果包含了所有主效应和交互效应,那么检验结果与“饱和”模型完全一致;但是在“构建项”选择进入模型的项目时要按照主效应、低阶交互项、高阶交互项的顺序,否则结果将不一致。