在无金标准的诊断试验——Deming回归一文中,如果没有重复测量的数值,也可使用重复测量的变异系数(coefficient of variation, CV)进行代替原始数据进行Deming回归分析,本文将实例介绍重复测量的变异系数在MedCalc软件中的实现过程。
关键词:MedCalc; 重复测量; 变异系数; CV。
在测量研究中,对象内的差异是不均匀的,而且与测量值呈一定的比例,此时需要计算对象内的变异系数。两次测量中的变异系数(coefficient of variation from duplicatemeasurements)可用于计算对不同对象或材料进行两次测量的变异系数,以便确定两次测量(或替代方法)的重复性,并估计运行内部的不精确性。
一、案例介绍
某公司新购入两台不同的仪器,为确保新旧仪器测得的某生化指标的等价性或一致性,因此使用这3台仪器同时测量了14名正常志愿者的某生化指标,试分别计算新仪器1与老仪器、新仪器2与老仪器两次测量的变异系数。部分数据见图1,本案例数据可从“附件下载”处下载。
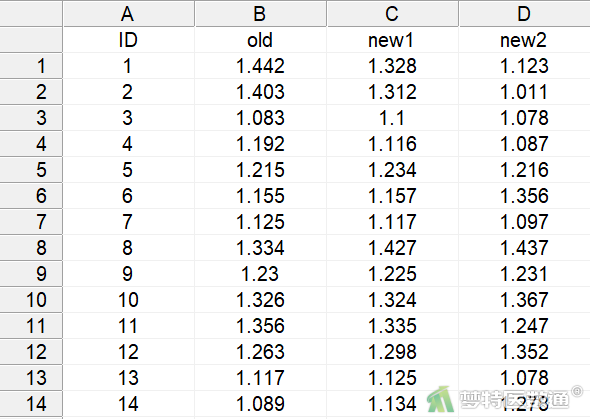
二、案例分析
本案例的目的是分析两台新仪器与老仪器的测量结果是否一致,需要计算对不同对象或材料进行两次测量的变异系数(CV),以便确定两次测量(或替代方法)的重复性,并估计运行内部的不精确性。
三、软件操作及结果解读
(一) 软件操作
选择“统计”—“方法对比和评估”—“重复测量中的变异数据”(图2)。
在“重复测量中的变异系数”对话框,按图3设置相应参数:
- 第一次测量:本例选择“old”。
- 第二次测量:本例选择“new1”。
- 方法:可选择以下3种方法计算CV:
1. 均方根法(汉化后的软件错译为“方均根法”)
公式为:
\(C V(\%)=100 \times \sqrt{\frac{\sum\left(\frac{d}{m}\right)^{2}}{2 n}}\)其中d为两个配对测量值的差值,m为配对测量值的平均值。当1对或以上的配对测量值的平均值为0时,不能使用该方法。
2. 对数法
首先计算观测值对数的差值平方和:
\(s l=\sum\left(\ln x_{1}-\ln x_{2}\right)^{2}\)然后计算:
\(C V(\%)=100 \times\left(e^{\sqrt{\frac{s l}{(2 n)}}}-1\right)\)当任意值为0或负值时,不能使用本方法。
3. 对象内标准差法
- 首先计算总平均值:
以及对象内标准差:
\(S D=\sqrt{\frac{\sum\left(x_{1}+x_{2}\right)^{2}}{2 n}}\)然后计算:
\(C V(\%)=100 \times \frac{S D}{\text { Mean }}\)当测量的总平均值为0时不能使用本方法。

重复上述步骤,计算新仪器2与老仪器两次测量的变异系数,得到的结果见表1。
(二) 结果解读
均方根法和对数法均计算两次测量中的CV及其95%CI,受试者内标准偏差法仅计算CV,3种方法得到new2与old两次测量中的CV均大于new1与old,相对于new2与old,new1与old的对象内变异更小,即new1与old的一致性更高,见表1。

四、结论
本研究使用重复测量的变异系数对两台新仪器与老仪器的一致性进行分析,由结果可认为新仪器1与老仪器之间的一致性更高。