对数线性模型(Log-linear Model)—理论介绍

关键词：对数线性模型; 一般对数线性模型; Logit对数线性模型; 分层对数线性模型

一、方法简介

对于分类变量，常用卡方检验进行数据分析，但卡方检验更多的应用于二维列联表的情形，若列联表维度更高，如要同时研究多个分类变量间的关系，卡方检验显然不够，因为它不可能为多个分类变量间的关系给出一个系统而综合的评价，也不可能在控制其他因素作用的同时，对变量的效应作出估计。此时，除了用logistic回归模型分析之外，也可以考虑采用对数线性模型这一多元统计分析方法来研究多个分类变量之间的关系。

对数线性模型将列联表资料中各个格子理论频数的自然对数表示为各个分类变量的主效应，以及各个分类变量之间交互效应的线性模型。通过迭代计算估计模型中的参数，应用方差分析的思想，检验各分类变量的主效应和交互效应的大小。此时，不区分因变量和自变量，强调的是模型的拟合优度检验和分类变量间交互效应的检验。

如以下案例中(表1)，探讨年龄(0=60岁以下，1=60岁及以上)和突出部位(1=单侧，2=中央，3=极外侧)与经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的关系，纳入146例治疗效果“不佳”(记录为1)的患者，278例治疗效果“良好”(记录为0)的患者。本案例数据可从“附件下载”处下载。

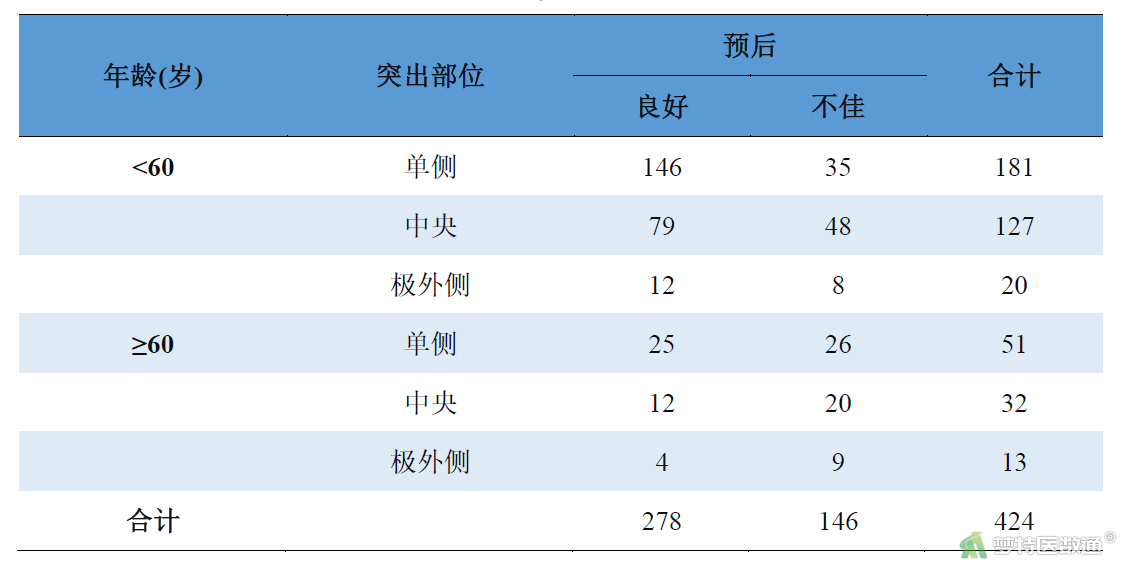
如果不考虑年龄的影响，对突出部位和预后总体上进行卡方检验可得到χ²=15.966，P<0.001；即突出部位和预后有关。如果考虑年龄的影响，分别对两个年龄组中突出部位和预后进行卡方检验，可发现在<60岁组突出部位和预后的关联有统计学意义(χ²=14.280，P=0.001)；但在≥60岁组突出部位和预后的关联无统计学意义(χ²=1.942，P=0.379)。可见基于不同年龄组条件下，突出部位和预后之间的关联不同。这是因为年龄和突出部位并不独立(χ²=5.920，P=0.052)，因此对于二维以上的列联表并不能简单的合并后进行卡方检验。

在上述案例中共有12个格子，424个频数。假设在该列联表中，分布属于随机变量，那么在总样本量、行合计、列合计和层合计均固定时，可以通过这种多项分布将每个格子期望频数的自然对数与分类变量之间建立线性模型，描述变量之间的关系，即对数线性模型。

二、模型构建

对数线性模型的构建一般以饱和模型开始，饱和模型包含了所有变量的主效应，低阶交互效应和高阶交互效应。在本案例中，饱和模型包括以下部分：

• 预后、年龄、突出部位3个主效应项；
• 预后*年龄、预后*突出部位、年龄*突出部位3个二阶交互效应项；
• 预后*年龄*突出部位1个高阶交互效应项。

对数线性模型为层次模型，如果模型中包含了某几个变量的高阶交互效应项时，这几个变量的低阶交互效应项与主效应项也一定包含在模型中。但由于饱和模型的理论频数完全拟合了实际频数，因此在实际应用过程中的意义不大，所以需要找到最简约的模型，对变量之间的关系进行解释。拟合优度检验过程中通过后退法(即最先对饱和模型中的最高阶交互效应项进行假设检验，然后依次向次高阶和低阶交互效应进行假设检验)逐渐排除没有统计学意义的项，最后得到最优简化模型。

确定最优简化模型后，通常用最大似然估计法对拟合的简化模型参数进行估计。最大似然估计利用多项分布的原理构造自然函数，再求对数似然函数。由对数线性模型的结构可以发现，该模型不仅可以解决两个因素是否相关的问题。还可以用来分析各因素主效应是否起作用。如在本案例中，如果要想知道“年龄”是否对“预后”起作用，则需要看“年龄*预后”交互项是否有统计学意义。

三、适用条件

对数线性模型的构建需要满足以下条件：

• 观测值之间是独立和随机的，所有的变量均为分类变量。
• 有充足的样本量，在对数线性模型中需要有>5倍于格子数的样本量，如3×3×2的列联表样本量至少为90。
• 基于一定理论频数的重复样本其实际频数的分布满足正态性，所有格子的理论频数应当>1，并不能有20%以上的格子的理论频数<5，否则会降低假设检验的效能。SPSS软件中有时通过给每一个格子加一个固定的值(常见为0.05)以解决理论频数较小的问题。但这种做法可能会使得检验效能下降。

四、应用

在实际应用过程中，对数线性模型的应用远不如Logistic回归普遍，其主要原因在于：

• 模型的解释较为复杂：对数线性模型中当变量较多时，模型会变得非常复杂，使得模型的解释较为困难。尽管SPSS软件在分层对数线性模型中提供了最优简化模型的选择过程，但是模型的复杂性的确限制了对数线性模型的应用和推广。
• 对数线性模型中没有明确定义的自变量和因变量，但在实际应用中，根据变量的实际意义可分为自变量和因变量。尽管Logit对数线性模型可以解决因果关系明确的模型构建，但正如上所述，在自变量较多时对数线性模型存在着固有的局限性。
• 对数线性模型只能分析分类变量之间的联系，不能分析连续性变量存在模型中，当有连续性变量时需要将其转化为分类变量。如果不能成功转化为分类变量，则需要考虑Logistic回归模型。

尽管对数线性模型存在一定的缺陷，但模型本身并无优劣之分，只有适用与否。当多个分类变量之间分不出因果关系，或研究者对变量之间的因果关系并不感兴趣，仅需分析变量之间的相互关系时更多使用对数线性模型，而较少使用Logistic回归模型。