危险度差 (risk difference, RD),又称归因危险度 (attributable risk, AR),队列研究或干预性研究的主要效应测量指标,是指暴露组/干预组与未暴露组/对照组结局发生率之差的绝对值。当以RD为效应量进行Meta分析,先通过Mantel-Haenszel法计算固定模型下的加权合并危险度差,之后通过异质性统计量计算随机效应模型下的汇总危险度差。本文将实例演示在MedCalc软件中实现危险度差的Meta分析相关操作。
关键词:MedCalc; Meta分析; 危险度差; 率
一、案例介绍
假定,为探究某经典名方对糖尿病所致肾损伤引起的蛋白尿的疗效,学生甲对近10年的相关文献进行检索和筛选,最终纳入了11篇文献。提取相关数据后,拟以RD为效应量进行Meta分析。部分数据见图1,本案例数据可从“附件下载”处下载。

二、案例分析
本案例的主要结局指标是某经典名方治疗蛋白尿的疗效,即是否好转。在MedCalc中可采用RD为效应量,通过风险差异的Meta分析对效应量进行合并与汇总。
三、软件操作及结果解读
(一)软件操作
- 打开“危险度差的Meta分析.mcl”数据文件。
- 选择“统计”—“元分析”—“风险差异”(图1)
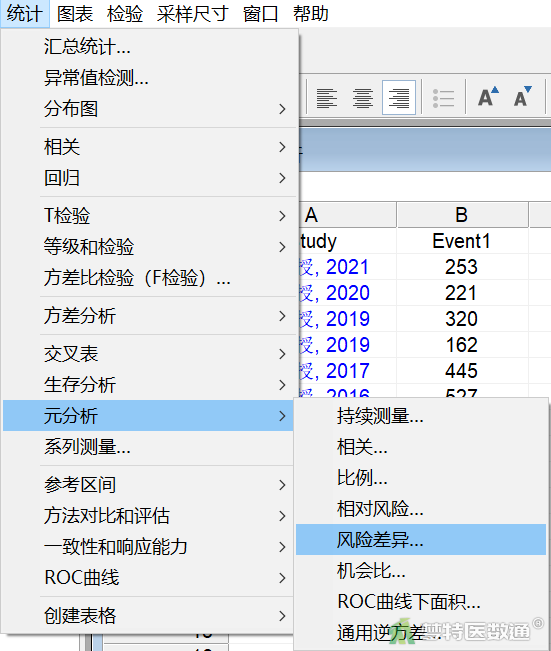
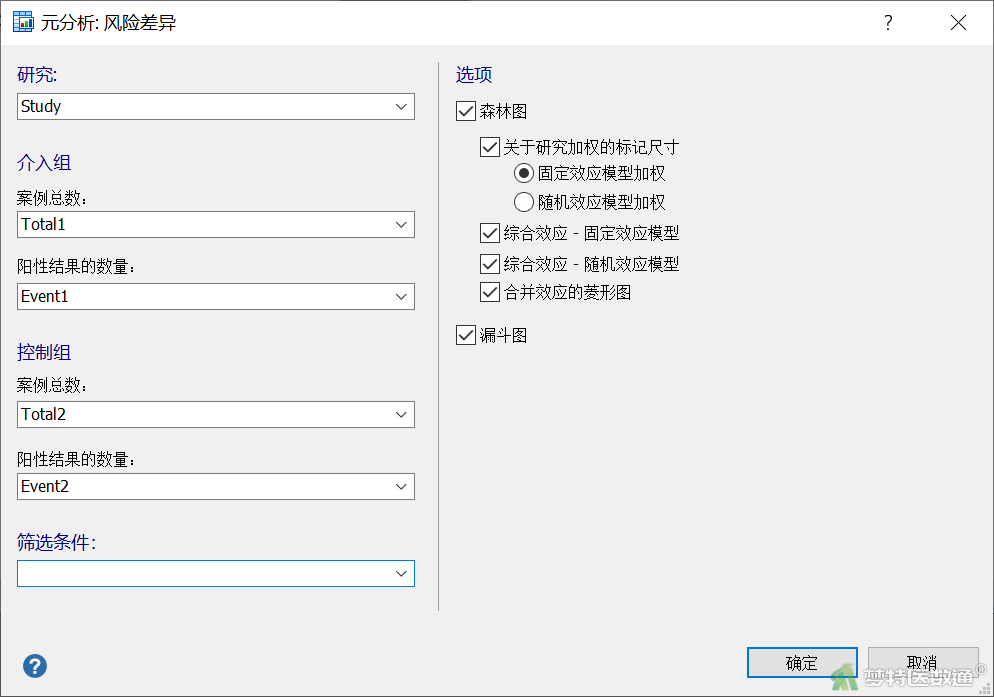
- 在“元分析:风险差异”对话框中,按照图2进行设置
- 研究:选Study
- 介入组:“案例总数”选Total1、“阳性结果的数量”选Event1
- 控制组:“案例总数”选Total2、“阳性结果的数量”选Event2
在MedCalc中进行危险度差的Meta分析,可同时得到固定效应和随机效应下的效应量总和,但固定效应模型加权和随机效应模型加权的选择,需要根据异质性检验结果而定。通常情况下,如果结果显示存在异质性,可选择总和(随机效应),反之选择总和(固定效应)。
(二)结果解读
1. 异质性检验
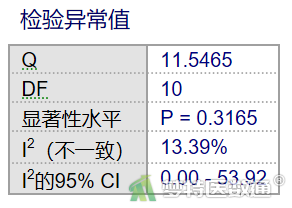
根据Q统计量为11.5465,P=0.3165,I2=13.39%(图3),按照常规的异质性检验标准P<0.10或者I2>50%,可认为各研究间不存在异质性,可选择固定效应模型分析结果。
2. 效应合并量
固定效应模型下合并的RD为0.0839,95%CI为 (0.0667~0.101),可认为经过Meta分析合并效应量,经典名方与对照药好转率的差值为8.38%,差异有统计学意义(P<0.001),结果见图4。

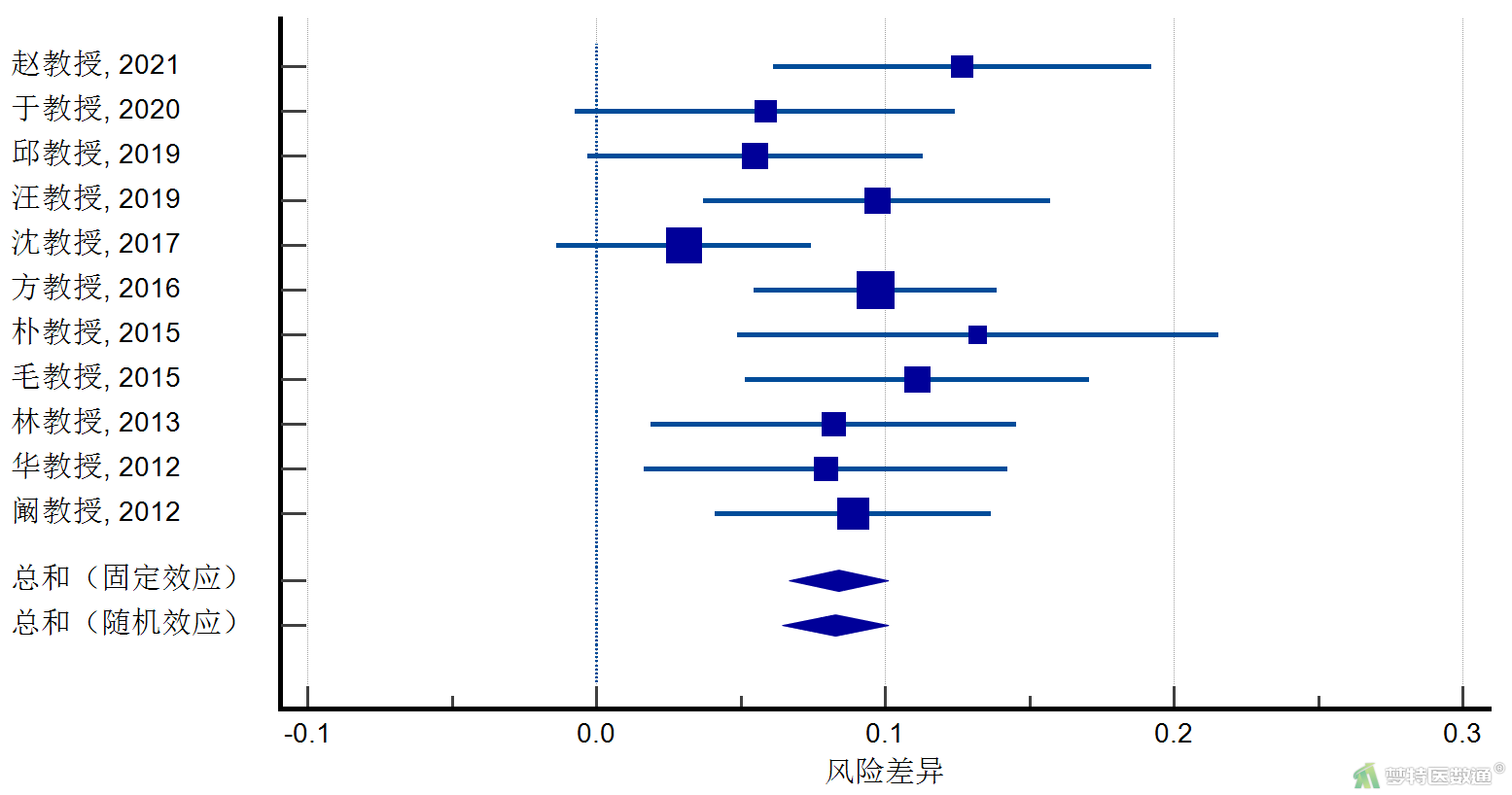
3. 森林图
森林图(图5)依次展示了11个研究的RD及其95%CI,固定效应模型下效应量总和为0.08左右,但是否有统计学意义需要参考效应合并量的具体结果表格(图4)。
4. 漏斗图
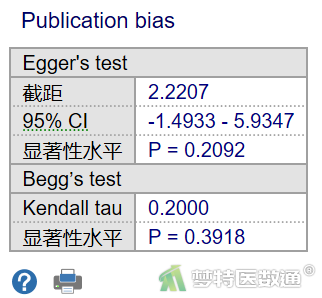
漏斗图主要用于观察Meta分析结果是否存在偏倚,如发表偏倚等,如果存在偏倚则漏斗图左右不对称,偏倚越大越不对称。由图6可知,本案例纳入的研究除1项在95%CI之外,其余均在加权汇总危险度差的95%CI,基本呈现对称分布,可认为该研究不存在偏倚 (或存在较小的偏倚)。此外,图7中的发表偏倚检验结果(Egger's检验)也提示本研究不存在显著的发表偏倚(P=0.2092)。一般当纳入研究少于20个时,Egger’s检验效能比Begg’s检验效能高,因此推荐此时当二者结果不一致的时候以Egger’s检验结果为主。

五、结论
本研究计算加权汇总危险度差,即加权汇总风险差异,异质性检验结果提示各研究间不存在显著异质性(P=0.3165,I2=13.39%),故选择固定效应模型进行效应量合并。经过Meta分析,该药物的加权汇总危险度差异为8.39%,95%CI为6.67%~10.10%。Egger's检验以及漏斗图均提示不存在明显的发表偏倚。