比值比(Odds Ratio)——Stata软件实现

关键词：Stata; 比值比; 数据加权; OR值

一、案例介绍

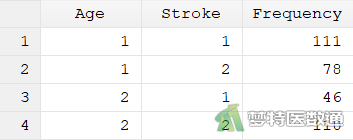
某研究员欲探究患脑卒中(Stroke)的危险因素，在某地区抽样调查了345名35岁以上居民脑卒中的患病情况（第1组为患病、第2组为未患病），现将所有调查对象按照年龄是否≥60岁分为两组[第1组为老年组(≥60岁)、第2组为中年组(35-59岁)]，数据见图1。本文案例可从“附件下载”处下载。问老年人的脑卒中患病风险是中年人的多少倍？

二、问题分析

本案例的分析目的是计算老年人的脑卒中患病风险是中年人的多少倍，也就是计算老年人与中年人脑卒中患病的比值比(Odds Ratio，OR)。

本案例以独立样本χ²检验为例计算OR值，但需要满足2个条件：

条件1：自变量和因变量均为二分类变量，本案例中的年龄分组和脑卒中患病情况均为二分类变量，满足该条件；

条件2：独立性，即观测值之间互不干扰，本案例的观测间相互独立，满足该条件。

三、软件操作及结果解读

(一) 适用条件判断

本案例数据满足上述条件。

(二) 统计描述及推断

1. 软件操作

①χ²检验

tabi 111 78\46 110,expected column all

 ②计算OR值

csi 111 78 46 110, or

2. 结果解读

(1) 统计描述

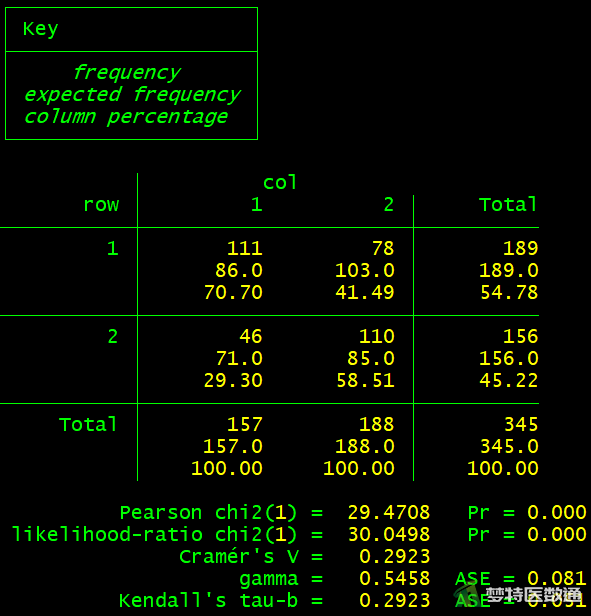
图2中给出了患脑卒中(Yes)和未患脑卒中(NO)两组人群中老年组(≥60岁)和中年组(35-59岁)的例数及百分比。由结果可知，患脑卒中的人群中老年组占70.70%，未患脑卒中的人群中老年组占41.49%。

(2) 统计学推断

解读χ²检验结果时，遵循以下原则：

①当总例数≥40，且所有期望频数(理论频数)≥5时，可使用Pearson χ²检验。

②当总例数≥40，有1个期望频数≥1且<5，可使用连续校正χ²检验。

③当总例数＜40或有1个期望频数＜1，需要使用Fisher确切概率法。

④无论总例数的大小及期望频数分布情况如何，Fisher确切概率法均可使用。在计算机能够满足运行负荷的情况下，推荐使用Fisher确切概率法。

⑤如果使用Pearson χ²检验或连续校正χ²检验得出的P值比较接近检验水准，建议采用Fisher确切概率法。

由图2可知没有单元格的期望频数少于5，最小期望计数为71.0。同时本案例样本数大于40，所以检验结果可采用“Pearson chi2 (卡方检验)”结果，患脑卒中和未患脑卒中两组人群中年龄构成的差异有统计学意义(χ²=29.471，P<0.001)。

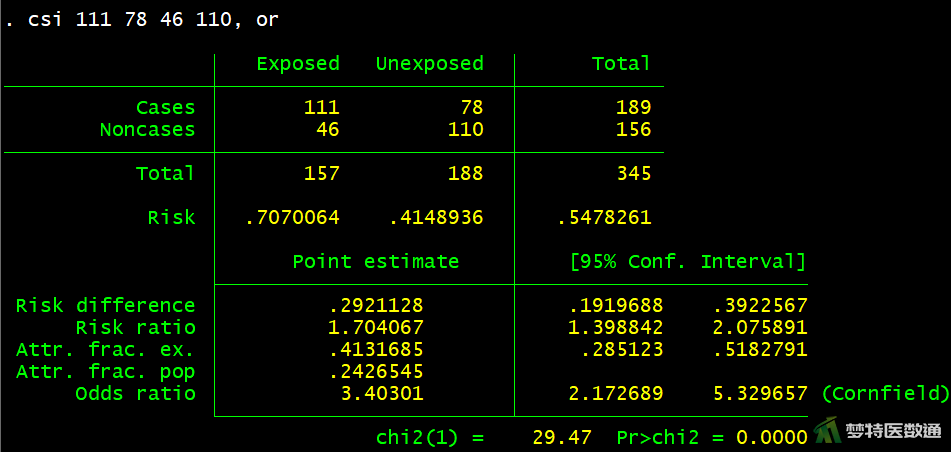
由图3的结果可知，老年组脑卒中的患病风险是中年组的3.403倍[OR=(111×110)/(78×46)]，OR值的95% CI为2.173~5.330。

四、结论

本研究采用2×2 χ²检验(独立样本χ²检验)计算比值比。结果显示，患脑卒中的人群中老年组占70.70%，未患脑卒中的人群中老年组占41.49%，老年人患脑卒中的风险是中年人的3.403 (95%CI: 2.173-5.330)倍，即高龄是脑卒中的危险因素。

五、知识小贴士

• 比值比，又称比数比、优势比，是病例组与对照组暴露比值之比(比值指某事物发生的可能性与不发生的可能性之比)。
• OR>1说明暴露与结局呈“正”关联，暴露是结局事件的促进因素。
• OR<1说明暴露与结局呈“负”关联，暴露是结局事件的抑制因素。

六、分析小技巧

• OR值的计算可以通过两种方法完成：一是采用独立样本χ²检验(Independent Samples χ² Test)。第二种是采用单因素二项logistic回归(Binary logistic regression)。
• 两种方法均可以得到OR值及其95%置信区间。OR值可信区间若包括1，则表明无统计学意义，其与P<0.05等价。
• 独立样本χ²检验中还可计算队列研究的相对危险度(RR)，在“Statistics (统计分析)”的“[Comparative Measures (2×2 only)](效应比较)”中勾选“Relative risk (相对风险)”即可。