在前面文章中介绍了“医学研究之单样本定性资料样本量计算——效应大小法”,若已知样本比例的置信区间宽度,还可以使用置信区间法计算样本含量。根据总体数量是否有限分为有限总体和无限总体置信区间法,本篇文章介绍使用单个比例的无限总体置信区间(Confidence Intervals for One Proportion)法计算样本量。
一、案例数据
某研究者设计了一份小学生营养膳食食谱,声称可让90%的小学生营养摄取量达标。某地教育局在引进该食谱前考察该食谱的效果,希望所选样本达标率可以代表所有学生水平,其估计误差不超过3%(置信区间上下限之差为6%),试估计所需的样本含量。
二、案例分析
营养摄入结果一般分为达标与未达标两种水平,资料服从二项分布,营养摄入达标率作为常用统计描述指标,且本案例中样本为随机样本,因此满足单样本卡方检验的要求。
本研究中,“所有学生”泛指无限总体的小学生,通过置信区间计算单样本比例的样本量可采用无限总体置信区间法,需要以下几个参数:
- 指定的双侧置信区间宽度,本例中为0.06。
- 检验水准α (通常取0.01至0.1,本研究取0.05)。
- 置信度/可信度CL(即1-α,常用0.95或0.99,本研究取0.95)。
- 预计样本比例值,本例中为0.9。
- 脱失率DR (通常不宜超过20%,本研究取10%)。
三、软件操作
(一) 方法选择
在左侧界面中依次选择“Procedures (程序)”—“Proportions (比例)”—“One Proportion (单样本比例)”—“ Confidence Interval (置信区间法)”—“Confidence Intervals for One Proportion (置信区间法检验单样本比例)”,见图1。
(二) 参数设置
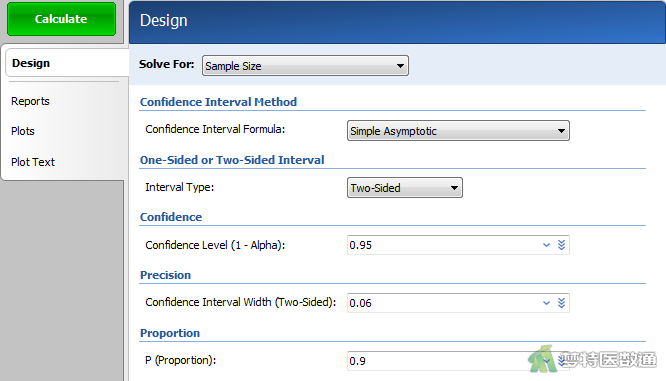
在“Design (设置)”模块中按以下参数设置相应选项(图2):
- Solve For: 选择“Sample Size”,表示本分析的目的是用于计算样本量。
- Confidence Interval Formula: 共有5种方法计算置信区间,本例选择“Simple Asymptotic”,适合极大的样本量计算。
- Interval Type: 选择“Two-Sided”,表示使用双侧置信区间。
- Confidence Level(1-Alpha): 表示置信度CL,即为1-α,填写“0.95”。
- Confidence Interval Width(Two-Sided): 即双侧置信区间宽度,为允许误差的两倍,本例填“0.06”。
- P(proportion): 表示假设样本比例的大小,此处填“0.9”。
(三) 脱失率设置
在“Reports (结果报告)”模块中,勾选“Show Dropout-Inflated Sample Size Report (报告脱失样本量)”,在“Dropout Rate”中填写“10%”(图3),表示按照10%的脱失率计算样本量。设置好上述参数后点击“Calculate (计算)”。

四、结果及解释
图4列出了该研究设计的相关参数和样本量计算结果,可知计算的样本例数(N)为385。

图5“References (参考文献)”列出了该计算过程中参考的相关文献;“Report Definitions (报告定义)”列出了各个参数的具体解释;“Summary Statements (报告概述)”为整个分析报告的摘要。

图6“Dropout-Inflated Sample Size (脱失样本量)”为考虑了脱失率的样本量(N'),也是研究实际开展过程中需要达到的最低样本量,本研究中为428。

图7为此次样本量估算整个过程的详细参数设置汇总。

五、结论
该案例为单样本比例的无限总体置信区间法计算样本量,已知预期的营养摄入达标率(样本比例的估计值)为0.9,预期的双侧置信区间宽度为0.03*2。若取检验水准0.05,则置信度为0.95,要使得所选样本达标率可以代表所有小学生水平,至少需要385例研究对象。若考虑10%的脱失率,则至少需要428例研究对象。