单样本Wilcoxon符号秩检验(One Sample Wilcoxon Signed Rank Test) —jamovi软件实现

关键词：jamovi; 非参数检验; 秩和检验; 单样本Wilcoxon符号秩检验; 单样本秩和检验

一、案例介绍

某地正常人尿氟含量的中位数为45.20 μmol/L。今在该地某厂随机抽取12名工人，测得尿氟含量。问该厂工人的尿氟含量是否与当地正常人的尿氟含量有差异？对数据的变量进行标签赋值后部分数据见图1。本文案例可从“附件下载”处下载。

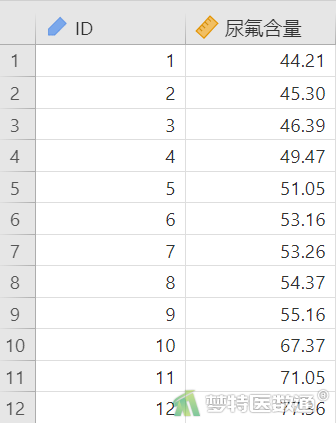
二、问题分析

本案例的分析目的是比较研究样本的水平是否与已知的总体中位数有差异，属于单样本设计的假设检验范畴。

三、软件操作及结果解读

(一) 适用条件判断(正态性检验)

1. 软件操作

① 选择“分析”—“ T检验”—“单样本T检验”，将变量“尿氟含量”选入右侧“因变量”框(图2)。

② 在“适用条件判断”中勾选“正态性检验”和“Q-Q图”(图3)，结果如表1和图4所示。

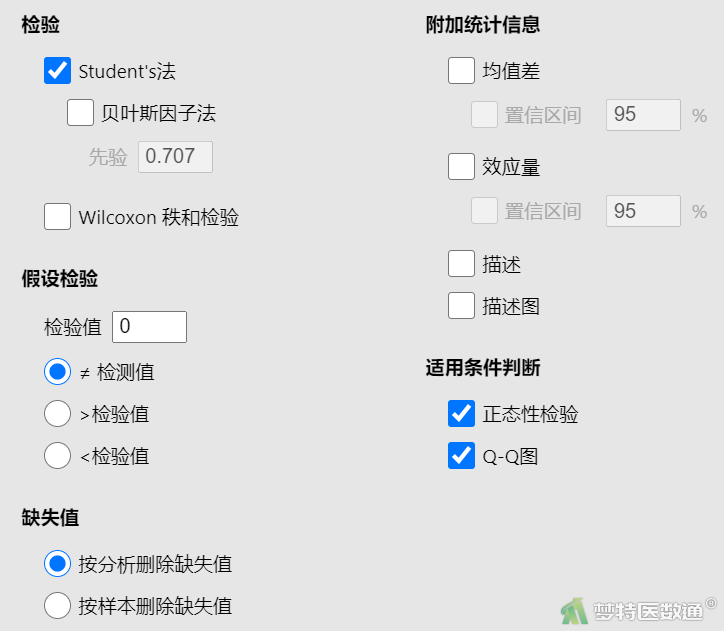
2. 结果解读

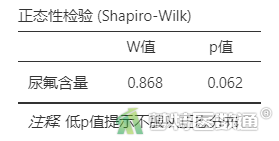
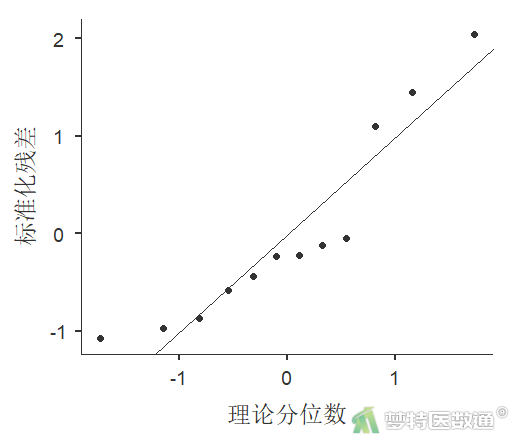
表1“正态性检验(Shapiro-Wilk)”结果显示P=0.062<0.1，提示数据不满足正态性条件(Kolmogorov-Smirnov适用于大样本)；图4 Q-Q图上散点与对角线的分布重合度较低，也可以认为数据为非正态分布。本案例宜选用单样本Wilcoxon符号秩检验。

(二) 统计描述及推断

1. 统计描述

(1) 软件操作

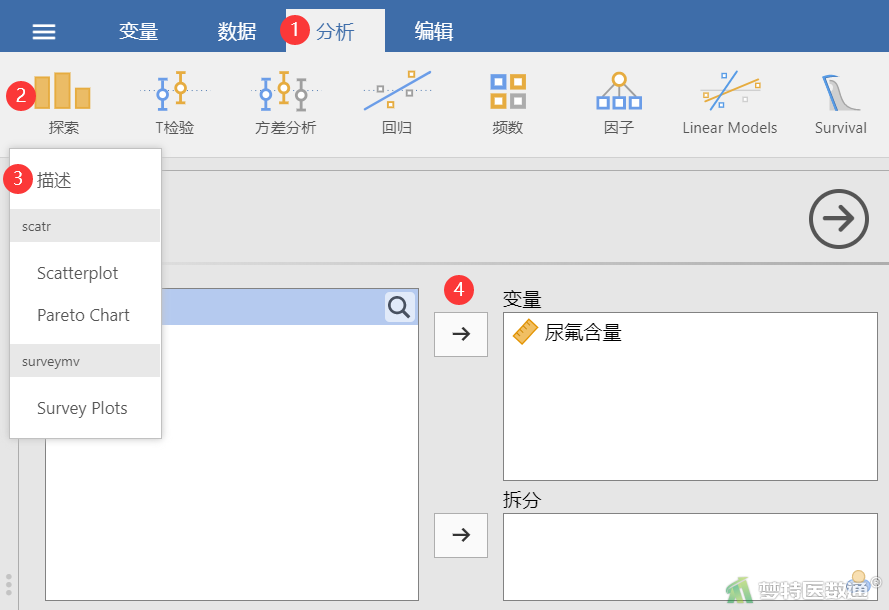
① 选择“分析”—“探索”—“描述”，将观察变量“尿氟含量”选入右侧“变量”框(图5)。

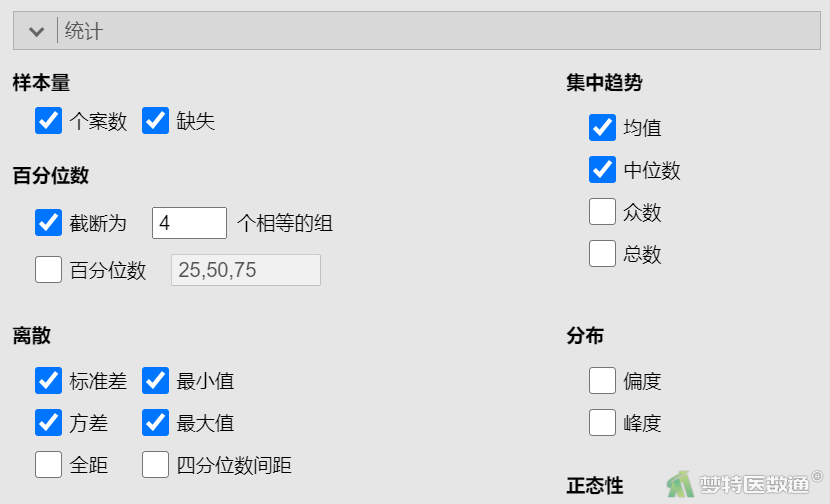
② 在“统计”下的“样本量”中勾选“个案数”、“缺失”，在“百分位数”中勾选“截断为4个相等的组”，在“集中趋势”中勾选“均值”、“中位数”，在“离散”中勾选“标准差”、“方差”“最小值”和“最大值”(图6)，结果如表2所示。

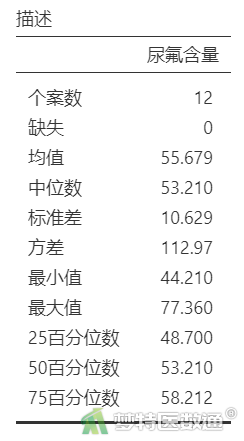
(2) 结果解读

表2“描述”提供了研究案例的“个案数”、“中位数”、“25百分位数”和“75百分位数”。可知，该厂工人的尿氟含量为53.210 (P₂₅~P₇₅：48.700~58.212) μmol/L。

2. 统计推断

(1) 软件操作

选择“分析”—“ T检验”—“单样本T检验”，在“假设检验”下的“比较值”中输入45.2，其他选项见图7，结果如表3所示。

(2) 结果解读

表3“单样本T检验”表格提供了“Student’s t”和“Wilcoxon W”两种方法分析的“统计量”、“自由度”、“P值”、“均值差”及其“95%置信区间”、“效应量”及其95%置信区间。由Wilcoxon符号秩检验结果可知，W = 76.000, P < 0.001，差异有统计学意义(P<0.05)，可以认为该厂工人的尿氟含量与当地正常人的尿氟含量水平有差异。“秩二列相关系数”为0.949，为强相关。

如果本案例采用“Student’s t”结果，t = 3.415，P=0.006，结果与Wilcoxon符号秩检验一致。

四、结论

本研究欲比较某厂工人的尿氟含量与当地正常人的尿氟含量水平是否存在差异，对该厂工人的尿氟含量进行正态性检验发现不符合正态分布，故选用单样本Wilcoxon符号秩检验。

经分析，该厂工人的尿氟含量为53.210 μmol/L (P₂₅~P₇₅：48.700~58.212)。采用单样本Wilcoxon符号秩检验分析显示：W = 76.000, P < 0.001，差异有统计学意义。秩二列相关系数为0.949，为强相关。本研究结果提示该厂工人的尿氟含量明显高于当地正常人的尿氟含量水平。

五、知识小贴士

• 计量资料的单样本设计假设检验，主要有单样本t检验和单样本Wilcoxon符号秩检验。对于计量资料，若不满足正态性或数据分布情况未知以及一端或两端是不确定数值时，应选用秩转换的非参数检验更为恰当。对于等级资料，常用非参数检验。
• 效应量的本质是衡量处理效应(或称实验效应)大小。秩二列相关系数是指分类变量与计量资料或等级资料之间的秩相关系数，用以衡量两种处理效应对应指标的相关程度，即效应量的大小，取值介于-1~1。绝对值越大则效应量越大。