医学研究之诊断实验的样本量计算——单组设计的灵敏度与特异性的置信区间法

关键词：样本量计算; PASS; 诊断试验; 灵敏度和特异度; 单样本诊断试验的样本量计算; 单样本灵敏度和特异度的置信区间

一、案例数据

某研究者欲评价一种新方法对某种癌症的诊断效果，已知该癌症的患病率为25%，通过查阅相关文献可知标准方法(病理活检)的灵敏度为85%，特异度为80%，希望新方法的灵敏度和特异度95%的置信区间宽度不超过0.06，试估计所需的样本含量？

二、案例分析

本研究是基于灵敏度和特异度检验的诊断试验用于评价诊断试验与金标准比较的结果，通过灵敏度和特异度置信区间估算样本量，则需要以下几个参数：

• 疾病患病率P，即研究目标人群中患有某病的预期比例或阳性个案的比例，本例为0.25
• 置信区间的宽度，即置信区间下限与上限之间的距离，本例为0.06
• 灵敏度，本例为0.85
• 特异度，本例为0.80
• 检验水准α (常取0.01至0.1)，本例取0.05
• 脱失率(DR，通常不宜超过20%)，本例取10%

三、软件操作

(一) 方法选择

在左侧界面中依次选择“Procedures (程序)”—“Sensitivity and Specificity (灵敏度和特异度)”—“Confidence Intervals for One-Sample Sensitivity and Specificity (单组设计灵敏度与特异度的置信区间)”，见图1。

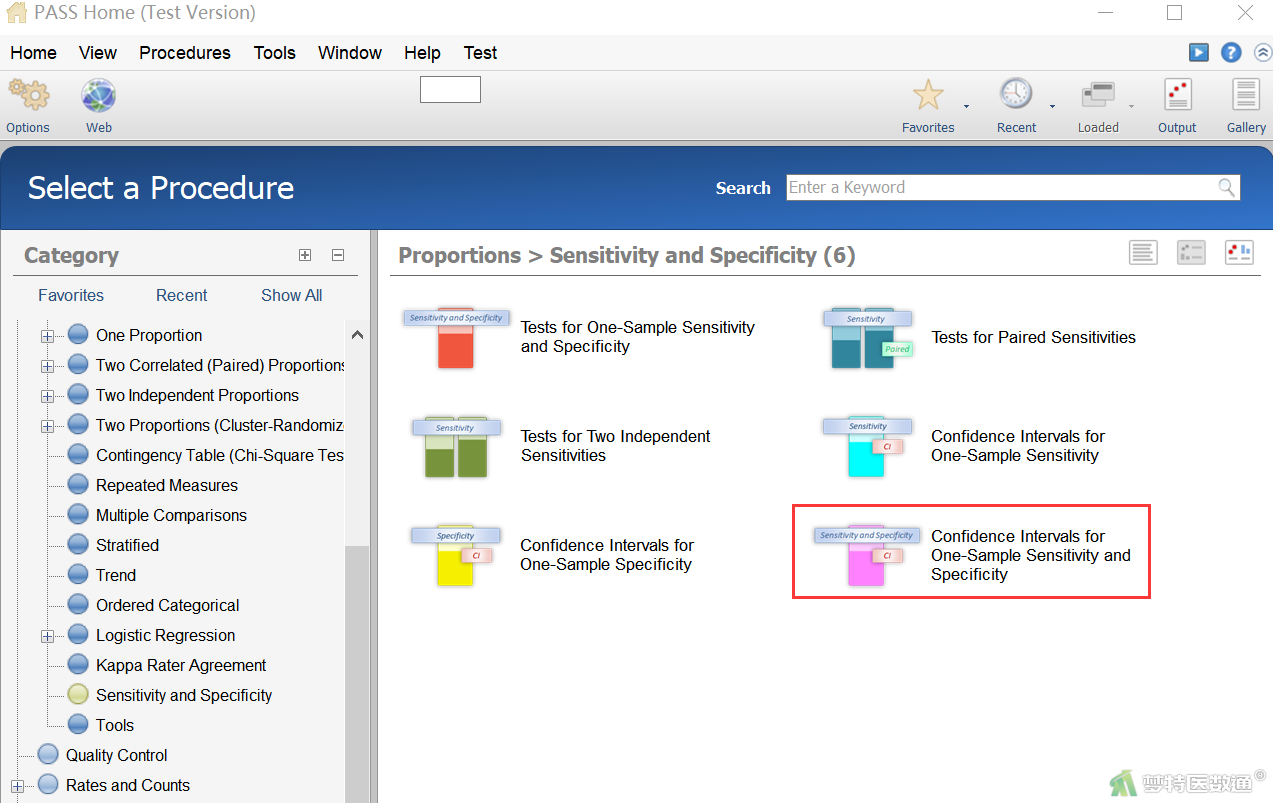
(二) 参数设置

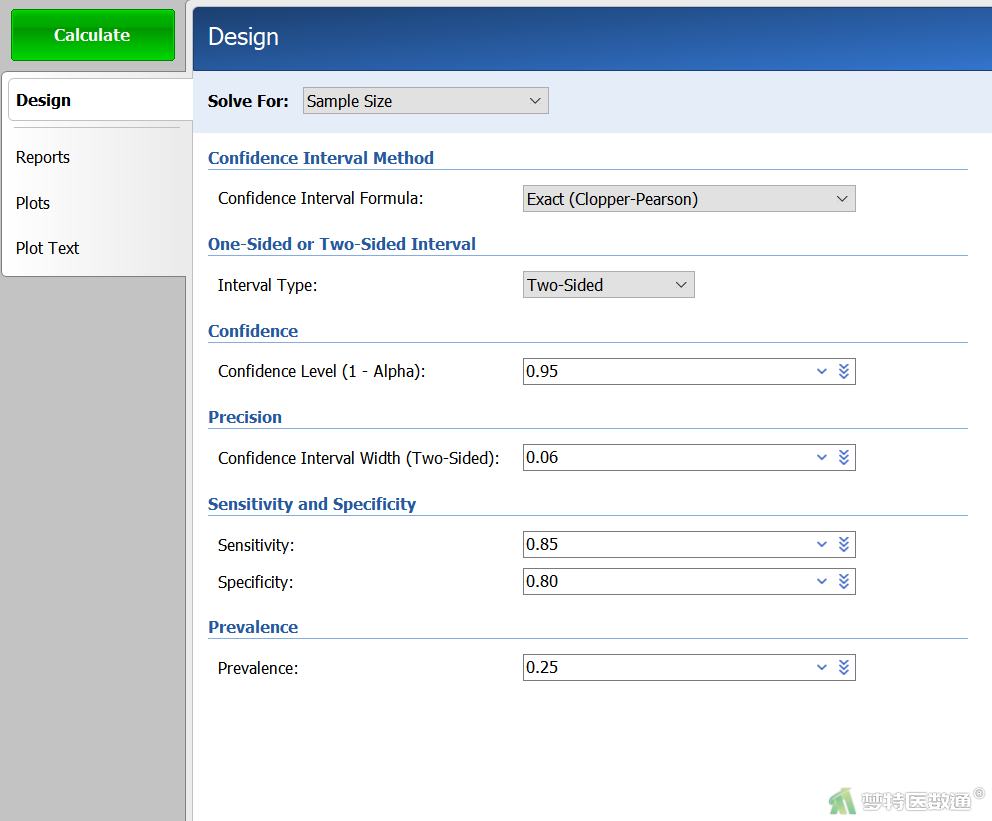
在“Design (设置)”模块中按以下参数设置相应选项(图2)：

• Solve For：选择“Sample Size”，表示分析的目的是计算样本量。
• Confidence Interval Method：“Confidence Interval Formula”表示置信区间公式，在PASS中有5种选择，“Exact (Clopper-pearson)”精确估计法(二项式概率)、“Score(Wilson)”临界比率转换、“Score(Contin.Correction)”连续性校正的临界比率转换、“Simple Asymptotic”二项分布正态近似法，仅适用于非常大的样本量、“Sample Asymptotic(Contin.Correction)”连续校正的二项分布正态近似法，本例选择“Exact (Clopper-pearson)”精确估计法(二项式概率)。
• One-Sided or Two-Sided Interval：“Interval Type”表示置信区间的类型，本例选择“Two-Sided”双侧置信区间宽度。
• Confidence：“Confidence Level (1-Alpha)”表示置信度，本例为0.95。
• Precision：“Confidence Interval Width (Two-Sided)”表示双侧置信区间的宽度。即从置信区间下限到上限的距离，本例为0.06。
• Sensitivity and Specificity：“Sensitivity”表示灵敏度，本例为0.85；“Specificity”表示特异度，本例为0.80。
• Prevalence：“Prevalence”表示疾病患病率，本例为0.25。

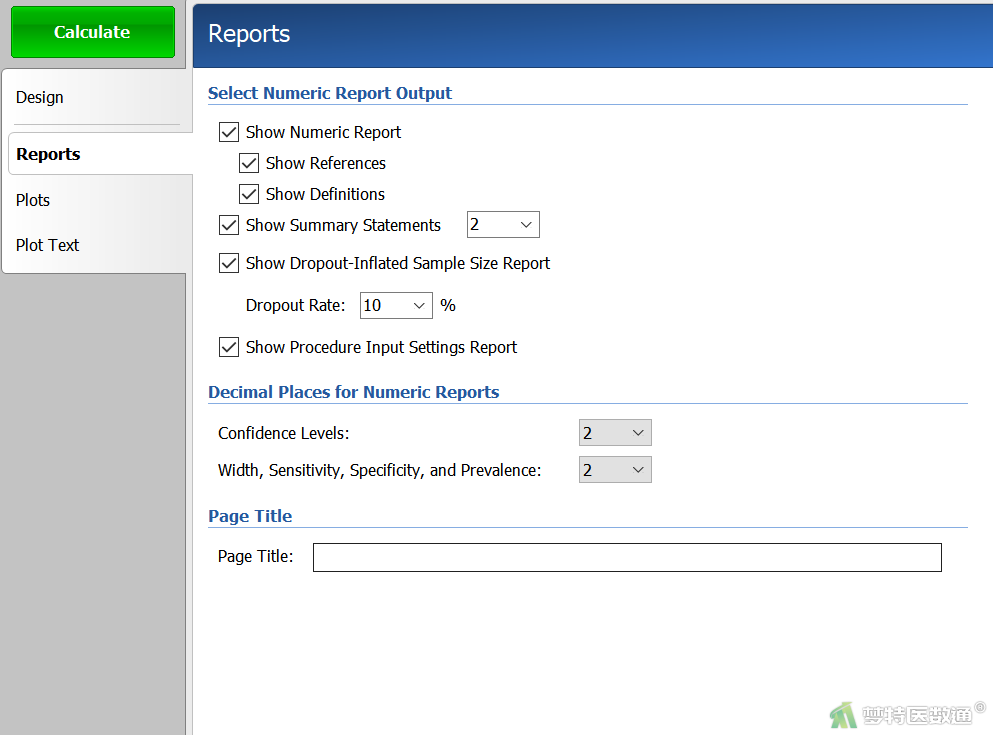
(三) 脱失率设置

在“Reports (结果报告)”模块中，勾选“Show Dropout-Inflated Sample Size Report (报告脱失样本量)”，在“Dropout Rate”中填10 (图3)，表示按照10%的脱失率计算样本量。设置好上述参数后点击“Calculate (计算)”。

四、结果及解释

图4列出了该研究设计的相关参数和样本量计算结果，可知计算的样本例数(N)为2304，其中患病人数N₁=N×P=2304×0.25=576，无病人数N₂=N×(1-P)=1728。

图5“References (参考文献)”列出了该计算过程中参考的相关文献；“Report Definitions (报告定义)”列出了各个参数的具体解释；“Summary Statements (报告概述)”为整个分析报告的摘要。

图6“Dropout-Inflated Sample Size (脱失样本量)”为考虑了脱失率的样本量(N')，也是研究实际开展过程中需要达到的最低样本量，本研究中为2560，其中患病人数N₁=N×P=2560×0.25=640，无病人数N₂=N×(1-P)=1920。

图7为此次样本量估算整个过程的详细参数设置汇总。

五、结论

本研究为单组设计的灵敏度和特异度置信区间的样本含量计算。已知某癌症的患病率为25%，通过查阅相关文献可知标准方法(病理活检)的灵敏度为85%，特异度为80%，希望希望新方法的灵敏度和特异度95%的置信区间宽度不超过0.06，则需要2304例研究对象，其中患病人数N₁=N×P=2304×0.25=576，无病人数N₂=N×(1-P)=1728。若考虑10%的脱失率，则至少需要2560例研究对象，其中患病人数N₁=N×P=2560×0.25=640，无病人数N₂=N×(1-P)=1920。