前面介绍了“医学研究之回归分析的样本量计算——二分类自变量条件Logistic回归的优势比检验”,本文介绍定量自变量条件Logistic回归的优势比检验(Tests for the Odds Ratio in a Matched Case-Control Design with a Quantitative X)的样本量估计。同样可用于匹配病例-对照设计,旨在检验疾病发生与风险因素(暴露变量)之间的关系。但不同的是该方法适用于计算自变量是定量资料的条件Logistic回归。
关键词:样本量计算; PASS; 回归分析; Logistic回归; 条件Logistic回归分析的样本量计算
一、案例数据
某研究者计划采用1:2匹配病例-对照设计研究心血管疾病与体质指数(BMI)的关联,同时收集另外3个其他影响因素,且另3个影响因素均为定量自变量。通过既往研究可知,研究对象的BMI标准差为2.0,BMI与心血管疾病之间的OR=1.3。若BMI在其他自变量上回归方程的R2=0.5,取α=0.05,β =0.1,试估计所需的样本含量?
二、案例分析
本研究为匹配病例-对照研究,欲调查一个因变量与多个定量自变量的关系,采用定量自变量条件Logistic回归,其样本量计算需要以下几个参数:
- 每组病例数与对照数,本例分别为1和2
- 暴露变量的估计标准差,本例为2.0
- 目标自变量与因变量之间的优势比,本例为1.3
- 暴露变量在模型中的其他自变量上回归时得到的方程的R2,本例为0.5
- 检验水准α (常取0.01至0.1),本例取0.05
- 检验功效1-β (常取0.8或更高),本例取0.9
- 脱失率 (DR,通常不宜超过20%),本例取10%
三、软件操作
(一) 方法选择
在左侧界面中依次选择“Procedures (程序)”—“ Regression (回归)”— “Conditional Logistic Regression (条件Logistic回归)”—“Tests for the Odds Ratio in a Matched Case-Control Design with a Quantitative X (单个定量自变量条件Logistic回归的优势比检验)”,见图1。

(二) 参数设置
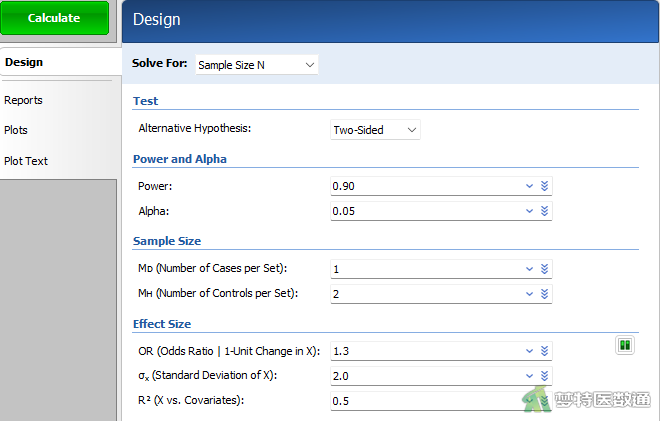
在“Design (设置)”模块中按以下参数设置相应选项(图2):
- Solve For:选择“Sample Size N”,表示本分析的目的是用于计算样本量。
- Alternative Hypothesis:选择“Two-Sided”,表示使用双侧备择假设。
- Power and Alpha:Power为把握度,填0.90;Alpha为检验水准,填0.05。
- MD (Number of Cases per Set):表示每组病例数,通常不大于5。本例填1。
- MH (Number of Controls per Set):表示每组对照数,通常不大于10。本例填2。
- OR (Odds Ratio | 1-Unit Change in X):即待检验的优势比。优势比表示X = x + 1时的患病概率与X = x时的患病概率之比。本例填1.3。
- σX (Standard Deviation of X): 即暴露变量X的估计标准差。本例填2.0。
- R2 (X vs. Covariates): 表示暴露变量在其他自变量上回归时得到的方程的R2,以此来研究加入其他自变量时对检验功效和样本量的影响。范围为0≤R2<1。本例填0.5。
(三) 脱失率设置
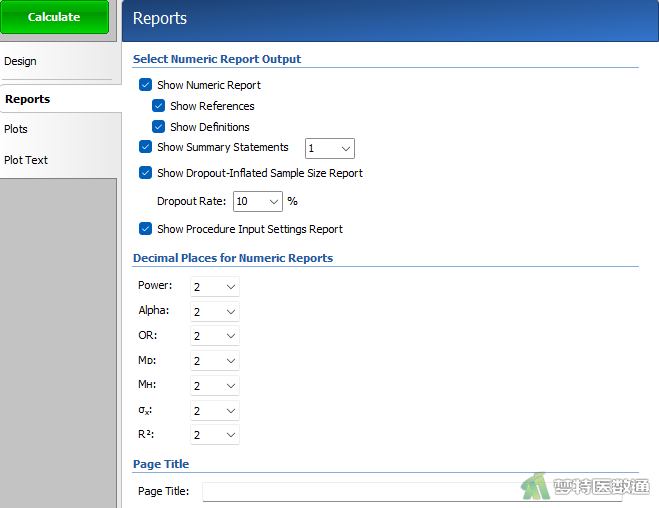
在“Reports (结果报告)”模块中,勾选“Show Dropout-Inflated Sample Size Report (报告脱失样本量)”,在“Dropout Rate”中填10 (图3),表示按照10%的脱失率计算样本量。设置好上述参数后点击“Calculate (计算)”。
四、结果及解释
图4列出了该研究设计的相关参数和样本量计算结果,可知计算的病例组所需样本例数(N)为115,则对照组所需样本例数为115×2=230。

图5“References (参考文献)”列出了该计算过程中参考的相关文献;“Report Definitions (报告定义)”列出了各个参数的具体解释;“Summary Statements (报告概述)”为整个分析报告的摘要。

图6“Dropout-Inflated Sample Size (脱失样本量)”为考虑了脱失率的样本量(N'),也是研究实际开展过程中需要达到的最低样本量,本研究中病例组需要的样本例数(N)为128,则对照组需要的样本例数为128×2=256。

图7为此次样本量估算整个过程的详细参数设置汇总。

五、结论
本研究为1:2匹配病例-对照设计,欲探究响应变量(心血管疾病)与暴露变量(BMI)和其他3个混杂变量是否存在关联。由于所有自变量均为定量变量,宜采用多因素条件Logistic回归。通过既往研究可知,研究对象的BMI标准差为2.0,BMI的OR=1.3,BMI在其他自变量上回归的方程的R2=0.5。若取检验水准0.05,检验功效0.90,病例组和对照组至少各需要115和230例研究对象。若考虑10%的脱失率,病例组和对照组至少各需要128和256例研究对象。