医学研究之回归分析的样本量计算——单个二分类自变量Logistic回归的优势比Wald检验

关键词：样本量计算; PASS; 回归分析; Logistic回归; 单个二分类自变量Logistic回归分析的样本量计算

一、案例数据

某研究者欲在开展一项探索肺癌与吸烟之间关系的研究，研究对象为成年男性，假设基线癌症事件率为6%，若研究者设定优势比(OR)为9.6，已知有52%的成年男性吸烟。进行Wald检验，取双侧α=0.05、β=0.10，试估计所需要的样本含量？

二、案例分析

该研究探索肺癌与吸烟的关系，已知基线癌症事件率为6%，OR=9.6，且只有一个二分类自变量(吸烟)，估计所需样本量，宜采用单个二分类自变量Logistic回归的优势比检验，其样本量估算需要以下几个参数：

1. 非暴露时事件发生概率P₀
2. 计算检验优势比的指标OR值或暴露时事件发生概率P₁
3. 样本比例，设定自变量X=1时的样本比例
4. 检验水准α (通用0.01至0.1)，本例为0.05
5. 检验功效1-β (常用0.80或更高)，本研究取0.90
6. 脱失率 (DR，通常不宜超过20%)，本例取10%

三、软件操作

(一) 方法选择

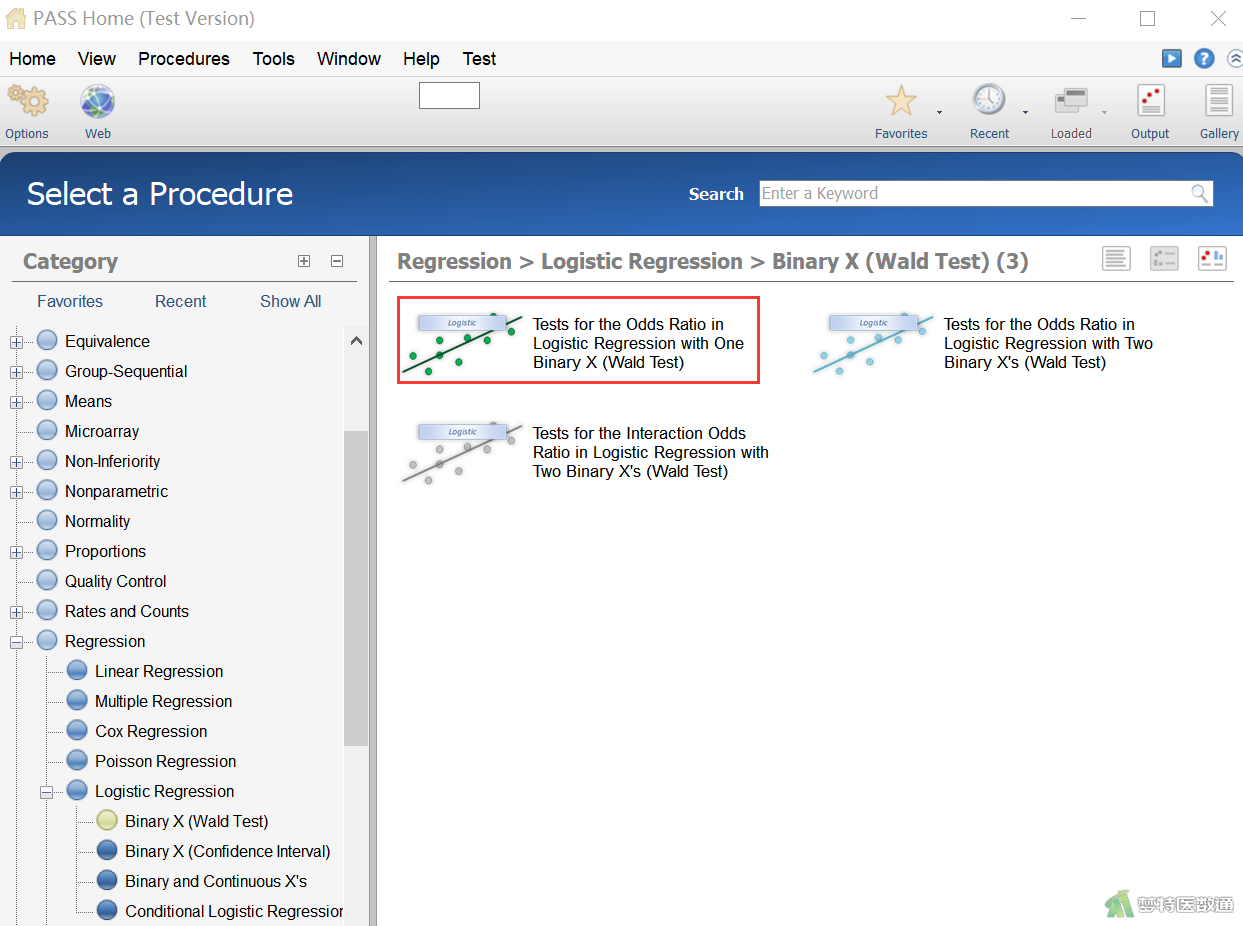
在左侧界面中依次选择“Procedures (程序)”—“Regression (回归)”—“Logistic Regression (Logistic回归)”—“Binary X (Wald Test) (二分类协变量的Wald检验)”—“Tests for the Odds Ratio in Logistic Regression with One Binary X (Wald Test) (单个二分类协变量Logistic回归的优势比Wald检验)”，见图1。

(二) 参数设置

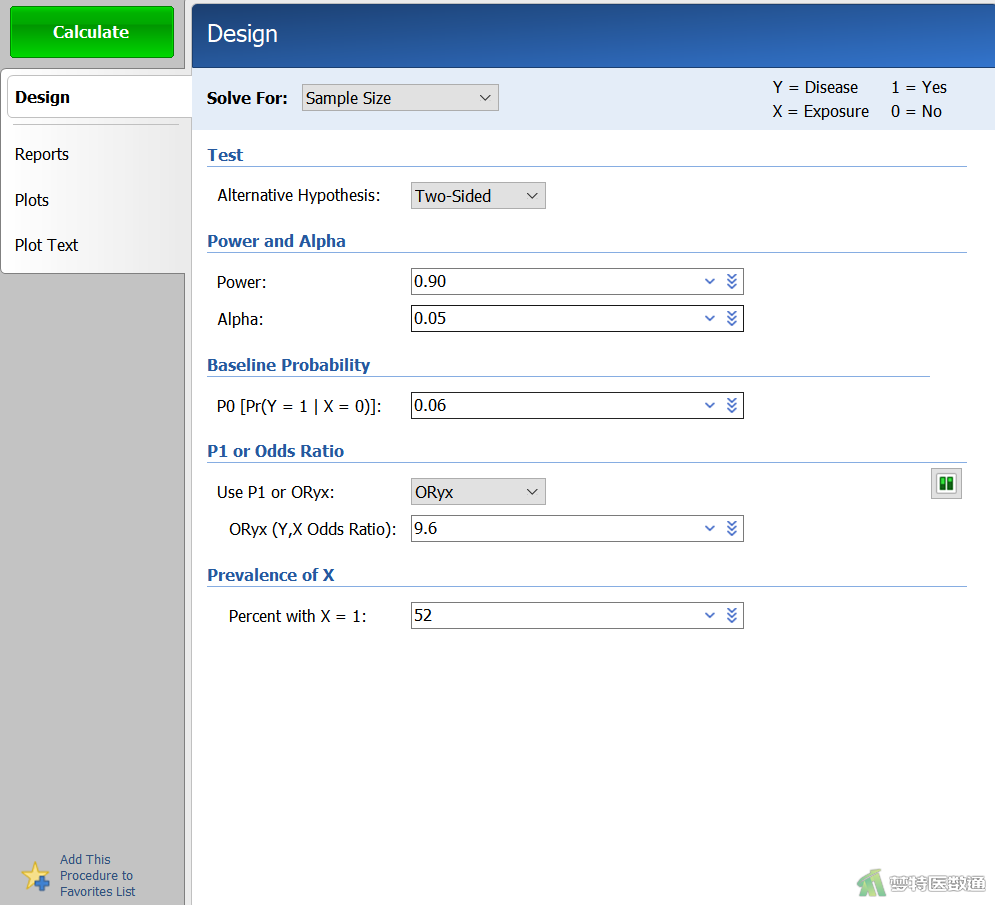
在“Design (设置)”模块中按以下参数设置相应选项(图2)：

1. Solve For：“Sample Size”表示本分析的目的是用于计算样本量。
2. Alternative Hypothesis：选择“Two-Sided”，表示使用双侧备择假设。
3. Power and Alpha：Power为把握度，填写“0.90”；Alpha为检验水准，填写“0.05”。
4. Baseline Probability：“P₀[Pr(Y=1|X=0)]”设非暴露时事件发生的概率π₀，本例为0.06。
5. P₁ or Odds Ratio：“Use P₁ or OR_yx”设定计算检验优势比的指标，可选择“P₁(暴露时事件发生概率)”或“OR_yx(优势比)”，本例选择“OR_yx”，OR=9.6。
6. Prevalence of X：设定X=1的样本比例。该值介于1~99之间，本例为52。

(三) 脱失率设置

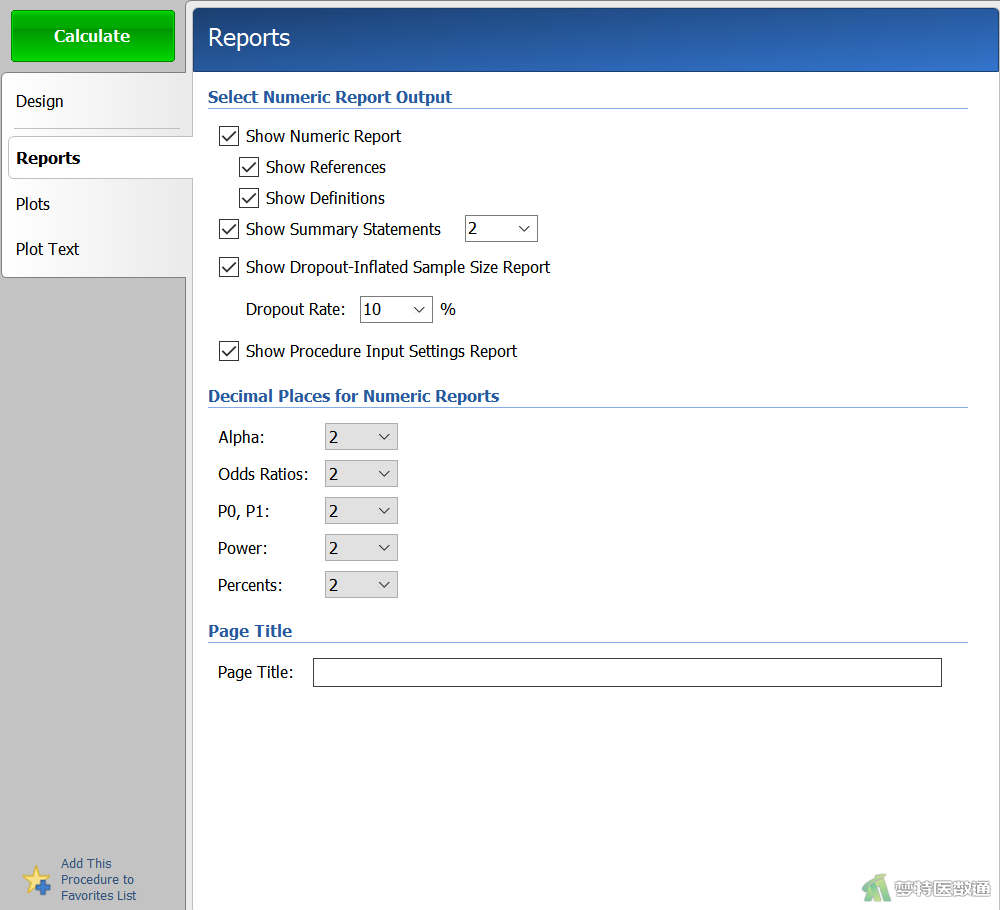
在“Reports (结果报告)”模块中，勾选“Show Dropout-Inflated Sample Size Report (报告脱失样本量)”，在“Dropout Rate”中填写“10%”(图3)，表示按照10%的脱失率计算样本量。设置好上述参数后点击“Calculate (计算)”。

四、结果及解释

图4列出了该研究设计的相关参数和样本量计算结果，可知计算的样本例数(N)为93。

图5“References (参考文献)”列出了该计算过程中参考的相关文献；“Report Definitions (报告定义)”列出了各个参数的具体解释；“Summary Statements (报告概述)”为整个分析报告的摘要。

图6“Dropout-Inflated Sample Size (脱失样本量)”为考虑了脱失率的样本量(N')，也是研究实际开展过程中需要达到的最低样本量，本研究中应至少为104例研究对象。

图7为此次样本量估算整个过程的详细参数设置汇总。

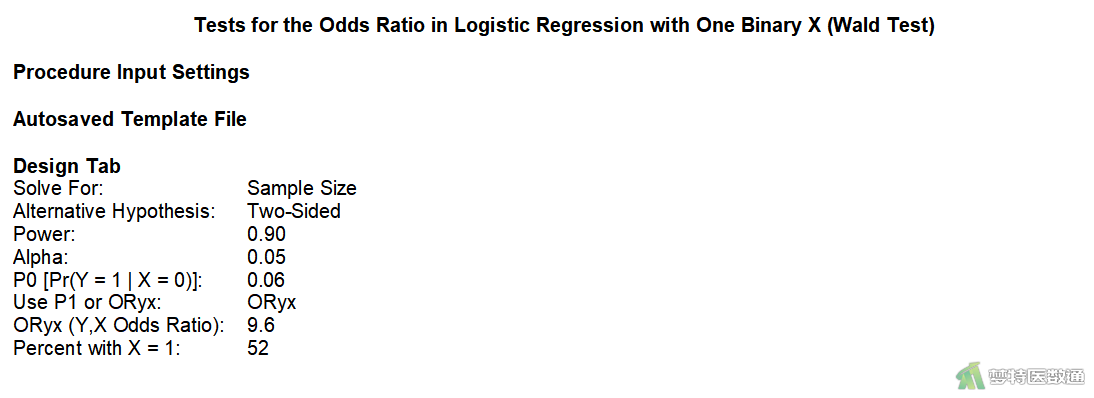
五、结论

该案例为单个二分类自变量Logistic回归的优势比Wald检验样本含量计算。研究对象为成年男性，已知基线癌症事件率为6%，OR=9.6，有52%的成年男性吸烟。进行Wald检验，取α=0.05、β=0.10，则至少需要93例研究对象。若考虑10%的脱失率，则至少需要104例研究对象。