R×C卡方检验(R×C χ² Test)——SPSS软件实现

关键词：SPSS; 列联表卡方检验; 多个率比较; 关联性检验; 列联系数

一、案例介绍

某科室回顾性研究推拿疗法、药物疗法和针灸疗法3种疗法治疗腱鞘炎的疗效。问3种疗法的有效率有无差别以及疗法与效果的关联(分为有效和无效)？

首先进行数据录入，χ²检验的数据录入可分为两种：第一种为频数资料，需要设置分组变量、观察变量和频数变量，该形式在进行χ²检验时较为常见，进行统计分析前需要进行数据加权。第二种为非频数资料，只有分组变量和观察变量两列，每一行为一个患者的数据，该形式是在SPSS软件中进行各种统计分析最常用的资料形式，进行χ²检验前不需要进行数据加权。

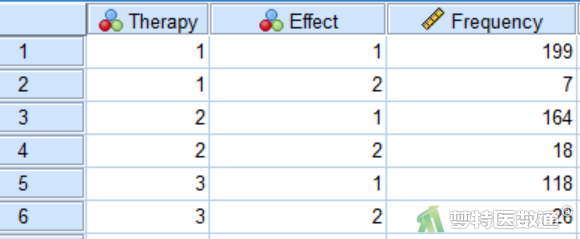
本案例的数据采用第一种录入方式。创建分组变量“Therapy”，测量尺度设为“名义”，赋值为“1”、“2”、“3”分别代表推拿疗法、药物疗法和针灸疗法。创建观察变量“Effect”，测量尺度设为“名义”，赋值为“1”和“0”分别有效和无效。创建频数变量“Frequency”，测量尺度设为“标度”，记录多种疗法下不同效果的患者数。对数据的变量和水平进行标签赋值后部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较三种疗法治疗腱鞘炎的疗效，也就是比较三组患者有效率的差异，同时分析两者的关联性。可以采用R×C χ²检验。但需要满足四个条件：

条件1：分组变量和观察变量均为分类变量，至少有一个无序多分类变量，且观察变量不是有序多分类变量。本案例的行变量疗法为无序三分类变量，列变量疗效为二分类变量，本案例数据满足该条件。

条件2：观测值之间相互独立，本案例的观测值均是相互独立，本案例数据满足该条件。

条件3：样本量足够大，要求每个格子内的期望频数均应>1，且期望频数<5的格子数不宜多于总格子数的1/5(如果期望频数太小，最好的办法是增加样本量以增加期望频数；若增加样本量有困难，则可使用Fisher确切概率法；若分组较多，可以合理的合并若干组，以增加期望频数)。

条件4：两个变量是同一随机样本的两种属性，本案例是回顾性分析腱鞘炎患者采用的疗法与效果的关联，所采用的疗法与效果均为已发生的事件，可以算作两种属性，该条件满足。

三、软件操作及结果解读

(一) 适用条件判断

本案例数据满足条件1、2和4，条件3的判断详见统计描述及推断。

(二) 统计描述及推断

1. 整体检验

(1) 软件操作

本案例为频数资料，需要先进行加权处理。

①选择“数据”—“个案加权”(图2)。

②出现“个案加权”对话框，选择“个案加权依据”后，将左侧变量“Frequency ”选入右侧“频率变量”框中，点击“确定”，则完成数据加权(图3)。

加权个案后进行检验。

③选择“分析”—“描述统计”—“交叉表”(图4)。

④ 出现“交叉表”对话框，将分组变量“Therapy”放入右侧“行”下方的变量框中，将结果变量“Effect”放入右侧“列”下方的变量框中(图5)，“行”和“列”中的变量可以互换位置，不影响检验结果。

⑤在“交叉表”对话框中点击右侧“统计”，出现“交叉表：统计”对话框，勾选“卡方”,在名义部分勾选“列联系数”和“Phi和克莱姆V”(图6)，点击“继续”回到“交叉表”对话框。

⑥在“交叉表”对话框中点击右侧“精确”，出现“确切检验”对话框，勾选“精确”，激活“每次检验的时间限制”，并默认已填写的数字“5”(图7)，点击“继续”回到“交叉表”对话框。

⑦点击“交叉表”对话框右侧“单元格”，在“交叉表：单元格显示”对话框中勾选“实测”、“期望”、“行”，其他保持默认不变，如图7所示。点击“继续”后回到“交叉表”对话框，点击“确定”，则得到卡方检验结果。

(2) 结果解读

图9为“疗法*疗效 交叉表”，给出了三种不同治疗方法不同治疗效果的观察值、期望频数及组内占比。由结果可知，推拿疗法、药物疗法和针灸疗法的有效率分别为96.6%、90.1%和81.9%。总例数为532例，每个格子的期望频数均大于5。

图10“卡方检验”给出了R×C χ²检验的统计量、自由度和P值。由图9中的总频数和每个格子的期望频数可知该案例数据满足条件3，图10下方的注脚a提示没有单元格的期望频数小于1，与图9结果一致。所以假设检验的P值可以取第一行的Pearson χ²检验结果，即三种疗法有效率的差异有统计学意义(χ²=21.038，P<0.001)。

图11“对称测量”给出了“列联系数”、“Phi(φ)”系数和“克莱姆V”系数，都是表示分类变量相关强度的指标。φ系数仅适用于2×2的数据格式，而克莱姆V系数的适用范围较广。这些系数的取值范围在0到1之间，数值越大相关性越强。当系数<0.1时为极弱相关，0.1~0.3时为弱相关，0.3~0.5时为中等相关，>0.5时为强相关。本案例中列联系数=0.195，P<0.001，克莱姆 V=0.199，P<0.001。结果表明，疗法与腱鞘炎的治疗效果为弱相关。

2.事后检验(两两比较)

对于R×C χ²检验，其结果只能说明各组的率或构成比整体上有无统计学差异，并不能说明哪两组之间的差异是否有统计学意义。因此，需要进行事后检验，即事后两两比较。在SPSS中既可以直接进行R×C χ²检验的事后两两比较的选项，也可以通过χ²分割法进行两两比较。卡方分割法即将三组率或构成比的比较拆分成多个两组率或构成比的比较；需要校正检验水准α'=α/m，其中m=k(k-1)/2，k为分组数。本案例为3个分组，拆分成3个两组率的比较；取α=0.05，则α=0.05/3=0.017。操作可以在上述步骤的基础上进行，其他选项不变，只需要首先进行分组的筛选。本文介绍卡方分割法如下：

(1) 软件操作

①选择“数据”—“选择个案”(图12)。

②出现“选择个案”对话框，选中“如果条件满足”后点击下方的“如果”(图13)，则出现设置个案选择条件的对话框(图14)。

图14左侧为变量列表，右侧上方为数值表达式文本框，用于设定筛选条件。其下方为软键盘，可以用鼠标按键输入数字和符号。函数列表位于软键盘右侧和下侧，分为“函数组”列表框，“函数和特殊变量”列表框和函数解释文字文本框3部分，可以在这里找到并使用所需的SPSS函数。

本案例的筛选条件较简单，仅需要对表示组别的变量“Therapy”进行设置。

③在数值表达式文本框内录入“Therapy<3” (图15)，点击“继续”后回到“选择个案”对话框，点击“确定”，则完成了个案选择的操作。此时选择的是推拿治疗组和药物疗法组，再重复整体检验的操作步骤③-⑦，则得到推拿疗法和药物疗法的有效率比较结果 (图16、图17、图18)。

④同理，选择个案时将数值表达式改为“Therapy>1”(图19)，即表示比较对药物组和针灸组，重复卡方检验的操作步骤后就可以得到这两组的比较结果(图20、图21、图22)。

⑤将数值表达式改为“Therapy~=2”(图23)，即表示比较推拿治疗组和针灸组，重复卡方检验的操作步骤后就可以得到这两组的比较结果(图24、图25、图26)。

(2) 结果解读

图16、图20和图24分别给出了三个组别进行两两比较时形成的交叉表，相应的观察频数、期望频数、有效率等。

图17、图21和图25“卡方检验”分别给出了推拿组与药物组、药物组与针灸组、推拿组与针灸组有效率的比较结果，P值分别为0.012、0.035、<0.001。可知，按照α'=0.017的检验水准，推拿组与药物组有效率的差异有统计学意义，药物组与针灸组有效率的差异无统计学意义，推拿组与针灸组有效率的差异有统计学意义。

图18、图22和图26给出了推拿组与药物组、药物组与针灸组、推拿组与针灸组进行两两比较的关联系数，φ分别为0.132、0.119、0.247，关联强度均较弱。

四、结论

本研究采用R×C χ²检验(R×C χ² Tests)对三种疗法治疗腱鞘炎的有效率进行比较，结果显示推拿疗法的有效率为96.6%、药物疗法的有效率为90.1%、外用膏药的有效率为81.9%，三种疗法有效率的差异有统计学意义(χ²=21.038，P<0.001)，表明三种疗法的有效率不全相同；疗法与效果的关联性为弱相关 (Contingency coefficient =0.195，Cramer’s V=0.199)。

采用χ²分割法，按照α'=0.017的检验水准进行两两比较，发现药物组与针灸组有效率的差异无统计学意义(P=0.035)。推拿组与药物组有效率的差异有统计学意义(P=0.012)，推拿组与针灸组有效率的差异有统计学意义(P<0.001)，两组的关联系数φ分别为0.132和0.247，关联强度均较弱。