本文将介绍点二列相关检验(Point Biserial Correlation Test)的样本量计算,该方法适用于以下两个变量间:一个为来自正态总体的等距或等比的计量资料;另一个为二分类变量,即按内容的某一性质分为两类相互独立的变量。点二列相关系数ρ是一个连续随机变量Y和一个二分类随机变量X间的乘积矩相关系数,如性别与量表得分间的关系,其样本量计算过程及注意事项如下。
一、案例数据
某大学英语老师欲研究学生性别与英语成绩的关系,他认为点二列相关系数ρ至少为0.45才能认为性别与英语成绩存在相关关系。取α=0.05,β=0.20,试估计该研究所需要的样本含量是多少?
二、案例分析
学生的性别为二分类变量,英语成绩可认为服从正态分布的计量资料,欲研究学生性别与英语成绩的相关关系,可采用点二列相关检验。点二列相关检验样本量估算,需要以下几个参数:
1. H1假设下的总体相关系数ρ1,本例为0.45 。
2. 检验水准α (通常取0.01至0.1,本例取0.05)。
3. 检验功效1-β (通常为0.80或更高,本研究取0.80)。
4. 脱失率DR (通常不宜超过20%,本例取10%)。
三、软件操作
(一) 方法选择
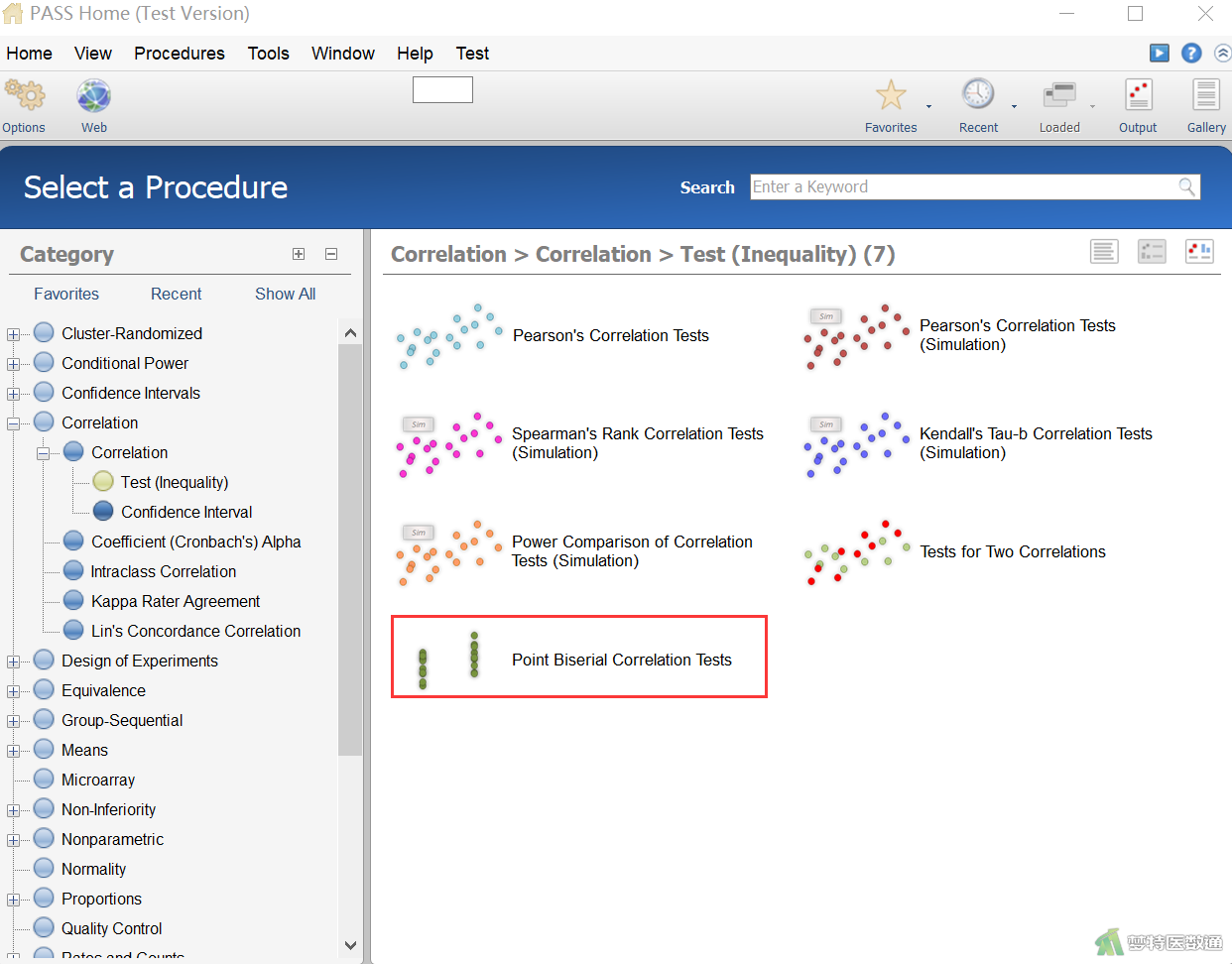
在左侧界面中依次选择“Procedures (程序)”—“Correlation (相关)”—“Test (Inequality) (非均衡性检验)”—“Point Biserial Correlation Tests (点二列相关检验)”见图1。
(二) 参数设置
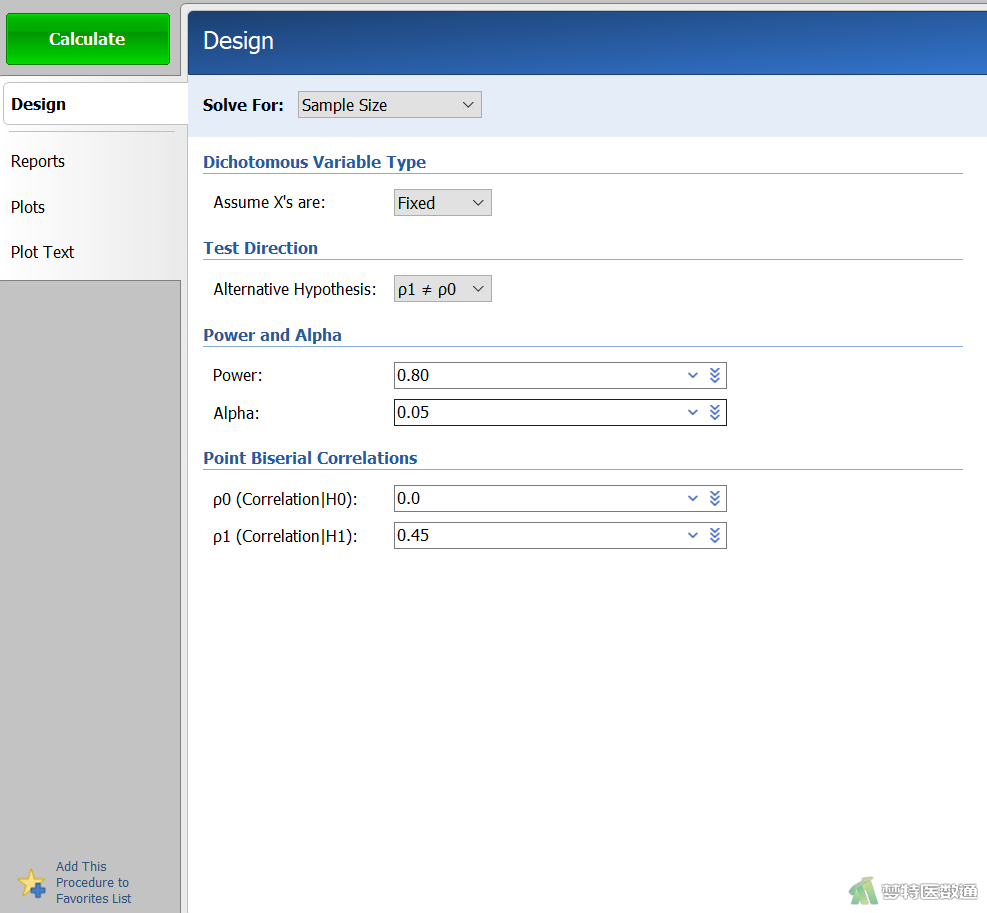
在“Design (设置)”模块中按以下参数设置相应选项(图2):
① Solve For:选择“Sample Size”,表示本分析的目的是用于计算样本量。
② Dichotomous Variable Type:“Assume X’s are”指定二分类变量X的类型,有两种选择:一种为“Random”表示随机设计,即X为偶然事件,另一种为“Fixed”表示固定设计,即X为试验者设定的(非随机事件),本例选择“Fixed”。
③ Test Direction:“Alternative Hypothesis”表示备择假设的检验方式,本例选择“ρ1≠ρ0”进行备择假设为H1:ρ1≠ρ0的双侧检验,为最常用的选择。
④ Power and Alpha:Power为把握度,填写“0.80”;Alpha为检验水准,填写“0.05”。
⑤ Point Biserial Correlations:“ρ0 ( Correlation|H0)”设定H0下的总体相关系数ρ0,该值必须介于-1~1之间,通常为0,本例填写“0.0”;“ρ1 ( Correlation|H1)”设定H1下的总体相关系数ρ1 ,该值也必须介于-1~1之间,本例填写“0.45”。
(三) 脱失率设置
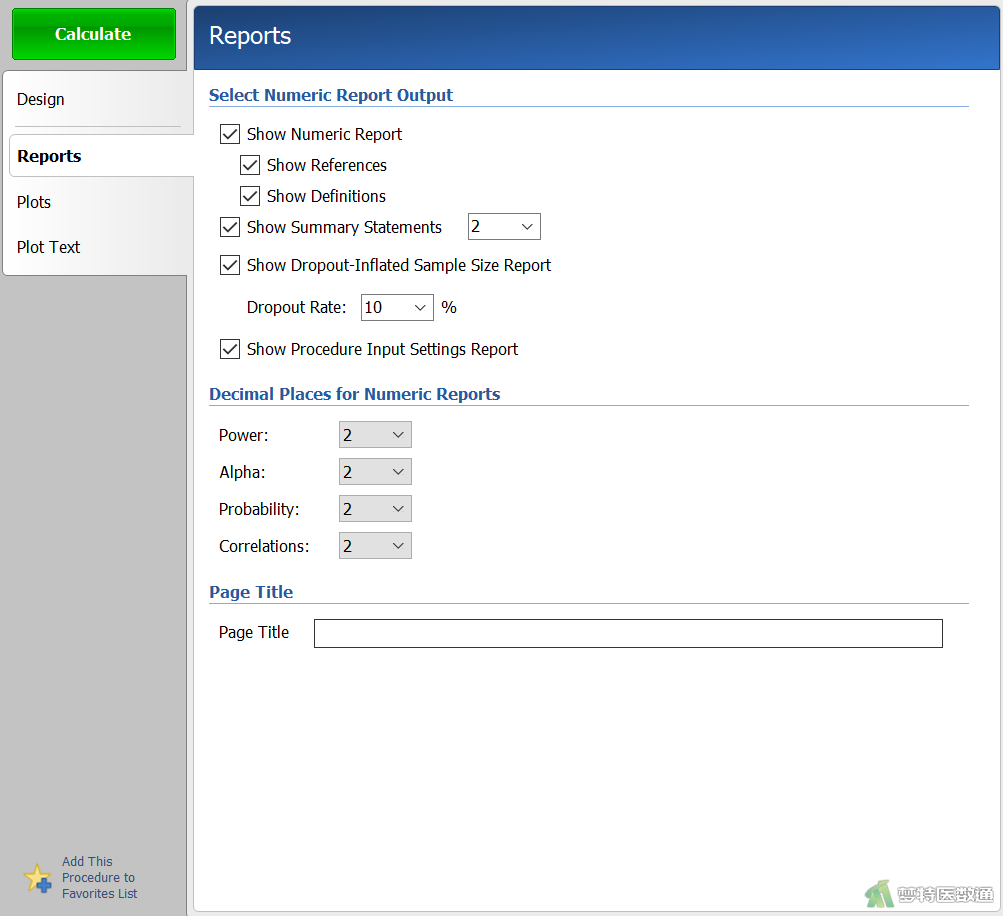
在“Reports (结果报告)”模块中,勾选“Show Dropout-Inflated Sample Size Report (报告脱失样本量)”,在“Dropout Rate”中填写“10%”(图3),表示按照10%的脱失率计算样本量。设置好上述参数后点击“Calculate (计算)”。
四、结果及解释
图4列出了该研究设计的相关参数和样本量计算结果,可知计算的样本例数(N)为33,即至少需要测评33名学生的英语成绩。

图5“References (参考文献)”列出了该计算过程中参考的相关文献;“Report Definitions (报告定义)”列出了各个参数的具体解释;“Summary Statements (报告概述)”为整个分析报告的摘要。

图6“Dropout-Inflated Sample Size (脱失样本量)”为考虑了脱失率的样本量(N'),也是研究实际开展过程中需要达到的最低样本量,本研究中至少需要测评37名学生的英语成绩。

图7为此次样本量估算整个过程的详细参数设置汇总。

五、结论
该案例为点二列相关检验的样本含量计算。已知备择假设下性别与英语成绩的点二列相关系数ρ1=0.45。若取检验水准0.05、检验功效0.80,则至少需要测评33名学生的英语成绩。若考虑10%的脱失率,则至少需要测评37名学生的英语成绩。