前面介绍了“医学研究之方差分析的样本量计算——F检验的多重比较法”,本文介绍最小有效剂量的Williams检验法(William’s Test for the Minimum Effective Dose)进行样本量估计。Williams检验可用于物质一系列剂量单调递增(或递减)的实验研究。这种研究的目的之一是确定最小有效剂量(有活性的最低剂量)。具体计算过程及注意事项如下。
一、案例数据
某研究设计了一个剂量-反应试验以探索某新型抗抑郁药物的最小剂量,设置了4个剂量组,包括1个安慰剂组(剂量为0)和3个药物活性剂量水平递增的实验组。以突触前转运蛋白的占有变化作为响应变量,以往研究表明组内标准差为22%,若期望出现差异的最小剂量变化为11%,取α=0.05,β=0.1,试估计所需的样本含量。
二、案例分析
本例通过Williams检验探索新型抗抑郁药物的最小剂量,从而比较对照组到最高剂量水平的药物的生物活性,需要以下几个参数:
1. 研究的组数,本研究为3。
2. 最小可检测差异,本研究为11。
3. 组内标准差,本研究为22。
4. 检验水准α (通常取0.01至0.1,本研究取0.05)。
5. 检验功效1-β (通常为0.80或更高,本研究取0.90)。
6. 脱失率DR (通常不宜超过20%,本研究取10%)。
三、软件操作
(一) 方法选择
在左侧界面中依次选择“Procedures (程序)”—“Means (平均值)”—“One-Way Designs(ANOVA) (单因素方差分析设计)”—“ Multiple Comparison (多重比较)”——“William’s Test for the Minimum Effective Dose”(最小有效剂量的Williams检验),见图1。

(二) 参数设置
在“Design (设置)”模块中按以下参数设置相应选项(图2):
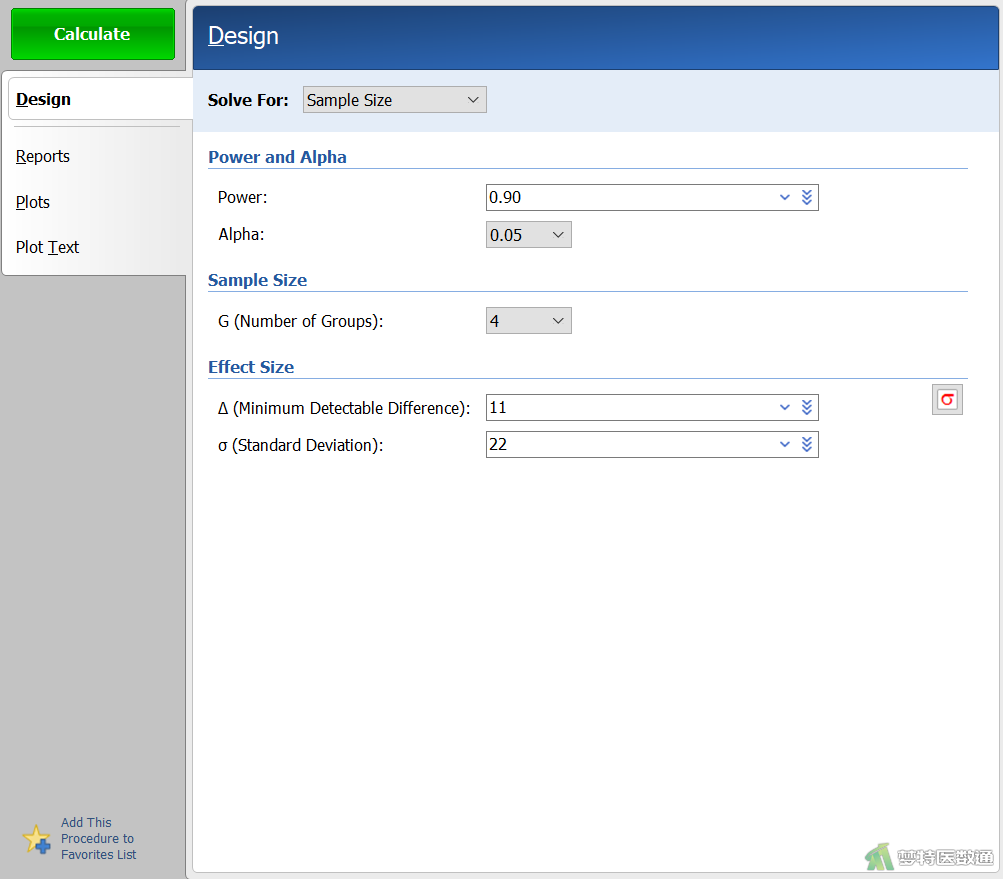
①Solve For:选择“Sample Size”,表示本分析的目的是用于计算样本量。
②Power and Alpha:Power为把握度,填写“0.90”;Alpha为检验水准,填写“0.05”。
③G(Number of Groups):包括对照组在内的研究组数,本研究为“4”。
④△(Minimum Detectable Difference):表示处理组与对照组平均值间具有临床意义的最小可检测差异,本例为“11”。
⑤σ(Standard Deviation):即组内标准差,当接受相同处理时受试者之间的可变性,填“22”。
(三) 脱失率设置
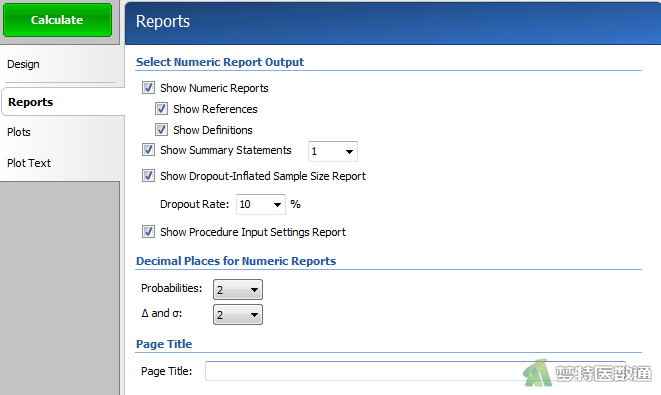
在“Reports (结果报告)”模块中,勾选“Show Dropout-Inflated Sample Size Report (报告脱失样本量)”,在“Dropout Rate”中填写“10%”(图3),表示按照10%的脱失率计算样本量。设置好上述参数后点击“Calculate (计算)”。
四、结果及解释
图4列出了该研究设计的相关参数和样本量计算结果,可知计算的各组样本例数为74,4组总例数(N)为296。

图5“References (参考文献)”列出了该计算过程中参考的相关文献;“Report Definitions (报告定义)”列出了各个参数的具体解释;“Summary Statements (报告概述)”为整个分析报告的摘要。

图6“Dropout-Inflated Sample Size (脱失样本量)”为考虑了脱失率的样本量(N'),也是研究实际开展过程中需要达到的最低样本量,本研究中4组总共至少需要332例研究对象,每组83例。
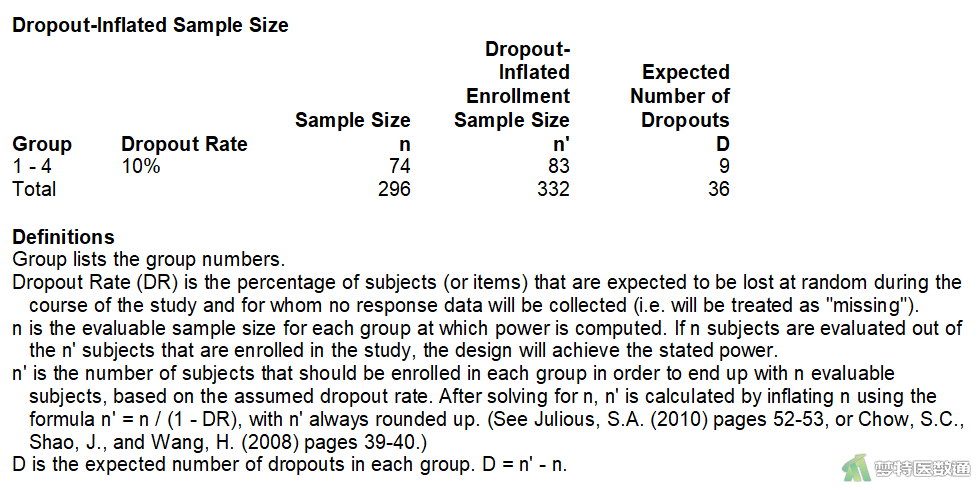
图7为此次样本量估算整个过程的详细参数设置汇总。

五、结论
该案例采用Williams检验进行最小有效剂量的计算样本量,已知有一个对照组和3个治疗组,药物剂量递增,以突触前转运蛋白的占有变化作为响应变量,以往研究表明组内标准差为22%,期望出现差异的最小剂量变化为11%。若取α=0.05,β=0.1,每组至少需要74例研究对象,4组共需296例研究对象。若考虑10%的脱失率,则至少共需要332例研究对象,每组83例。