竞争风险Cox回归 (Competing risk Cox regression)也称竞争风险模型(Competing risk model)是一种处理多种潜在结局生存数据的分析方法,早在1999年Fine和Gray就提出了部分分布的半参数比例风险模型,通常使用的终点指标是累积发生率函数(Cumulative incidence function, CIF)。本文实例介绍竞争风险模型在R软件中的实现步骤。
关键字:竞争风险模型;竞争风险Cox回归;Fine-Gray模型;Fine-Gray检验
传统的生存分析(Survival analysis)一般只关心一个终点事件(即研究者感兴趣的结局)。将发生结局事件前死亡的个体、失访个体和未发生结局事件的个体均按删失数据(Censored data)处理,要求删失情况与个体终点事件相互独立,结局不存在竞争风险。在实际情况中,某种已知事件可能会影响另一种事件发生的概率或者是完全阻碍其发生,则可认为前者与后者存在竞争风险。如,研究某治疗措施对非小细胞肺癌的疗效,感兴趣的结局事件是非小细胞肺癌导致的死亡,若随访过程中病人因为其他原因死亡,就观察不到感兴趣的结局事件,那其他原因的死亡则被认为是非小细胞肺癌死亡的竞争风险事件。竞争风险模型适用于多个终点的生存数据,是一种处理多种潜在结局生存数据的分析方法,通过计算每个结局的累积发生率函数(Cumulative incidences function, CIF)进行分析。本篇文章将实例演示在R软件中实现竞争风险Cox回归模型的操作步骤。
一、案例介绍
从SEER公共数据库中收集了1200例非小细胞肺癌患者数据,提取变量包括年龄、性别、种族、原位癌病发部位、T分期、手术类型、淋巴结检查数量、结局、随访时间。结局变量为三分类变量,包括生存(删失)、死于非小细胞肺癌患者、死于其他原因。目的为基于竞争风险模型下,研究淋巴结检查数量与非小细胞肺癌患者生存时间的关系,兴趣事件为患者死于非小细胞肺癌,竞争事件为死于其他原因(如其他肿瘤等)。数据变量见表1。
二、问题分析
本研究目的为探索淋巴结检查数量与非小细胞肺癌患者生存期的关系。结局变量为三分类,分别为生存(删失)、死于非小细胞癌、死于其他原因,故使用竞争风险模型较为合适。首先进行描述性分析,计算不同淋巴结检查数量组的感兴趣结局事件累积发生率,并使用Fine-Gray检验进行单因素组别比较。然后进行单因素竞争风险回归分析,将单因素分析结果有统计学意义的变量纳入多因素竞争风险模型进行校正,评估淋巴结检查数量与非小细胞肺癌患者生存时间的关系。竞争风险模型需要满足以下2个条件:
- 条件1:子分布满足等比例风险(Proportional hazards, PH)假定,该条件需要使用软件判断。
- 条件2:模型不存在严重多重共线性问题,该条件需要使用软件判断。
三、软件操作及结果解读
(一) 导入数据
mydata <- read.csv ('竞争风险模型.csv') #导入csv文件数据
View(mydata) #查看数据
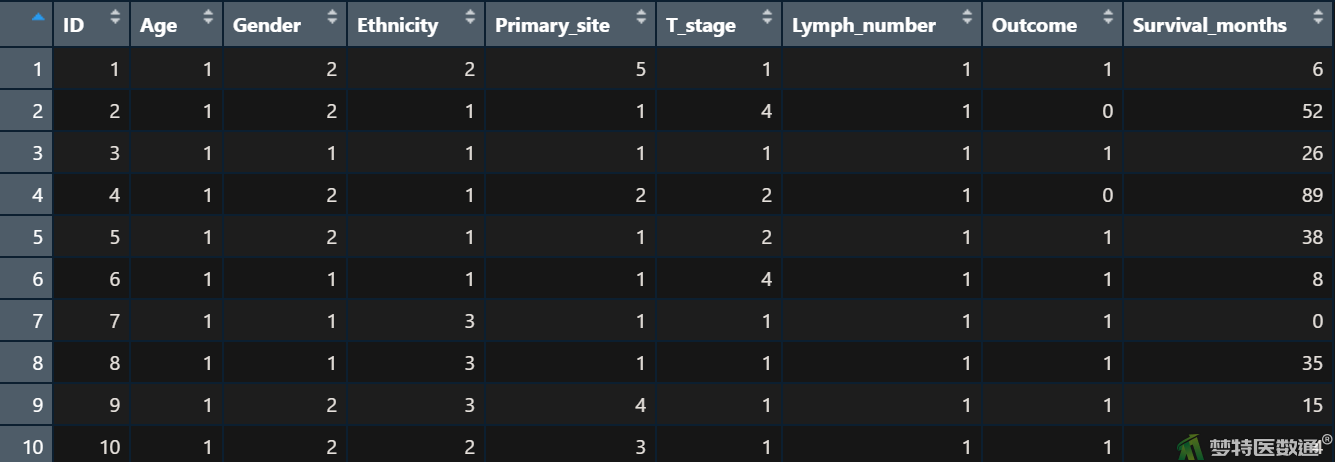
在图1数据栏目中可以查看全部数据情况,数据集中共有8个变量和1200个观察数据,具体信息见表1。
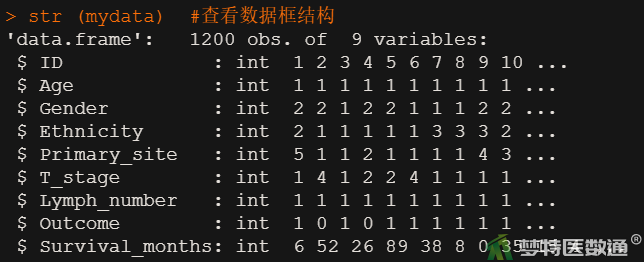
如果数据集较大也可使用如下命令查看数据框结构:
str (mydata) #查看数据框结构
(二) 数据整理
##给自变量添加标签label,并同时进行因子转换##
mydata$Age <- factor (mydata$Age, levels = c(1, 2, 3), labels = c ("<60 岁", "60-74 岁", "≥75 岁"))
mydata$Gender <- factor (mydata$Gender, levels = c(1, 2), labels = c ("Male", "Female"))
mydata$Ethnicity <- factor (mydata$Ethnicity, levels = c(1, 2, 3, 4), labels = c ("White", "Asian", "Black", "Others"))
mydata$Primary_site <- factor (mydata$Primary_site, levels = c(1, 2, 3, 4, 5), labels = c ("Upper lobe", "Middle lobe", "Lower lobe", "Main bronchus", "Overlapping lesion"))
mydata$T_stage <- factor (mydata$T_stage, levels = c(1, 2, 3, 4), labels = c ("T1", "T2", "T3", "T4"))
mydata$Lymph_number <- factor (mydata$Lymph_number, levels = c(1, 2), labels = c ("< 16", "≥ 16"))
mydata$Outcome <- factor (mydata$ Outcome)
(三) 统计分析
1. 描述性分析
(1) 软件操作
summary (mydata) #描述性分析并整理结果
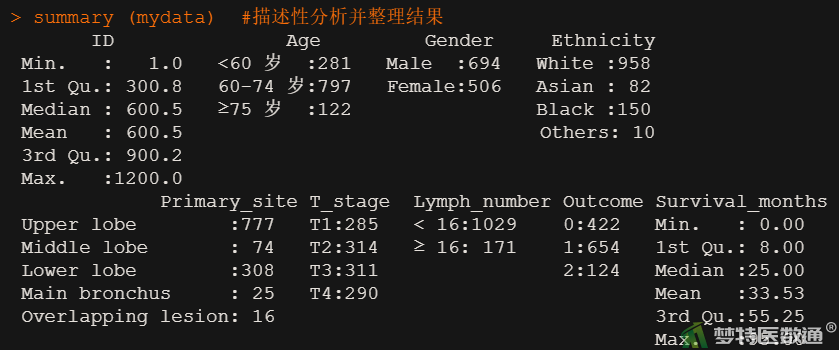
(2) 结果解读
共纳入1200例数据。其中男性694人,女性506人;白人958人,亚裔82人,黑人150人,其他种族10人;中位生存时间25 (8, 55.25)月;结局事件中,Censored组422例,Dead from NSCLC组654例,Dead from other causes组124例。
淋巴结检查数量<16组1029例,≥16组171例。
2.组别累积
(1) 软件操作
library (cmprsk) #加载cmprsk包 library (riskRegression) #加载pec包 library (pec) #加载pec包 cum_Lymph_number <- cuminc (mydata$Survival_months, mydata$Outcome, mydata$Lymph_number) #使用cuminc()函数进行单因素Fine-Gray检验 cum_Lymph_number #查看检验结果

cum_Lymph_number$`< 16 1`$est[length(cum_Lymph_number $`< 16 1`$est)] #计算Lymph_number第1个水平的感兴趣结局事件累积发生率 cum_Lymph_number$`≥ 16 1`$est[length(cum_Lymph_number $`≥ 16 1`$est)] #计算Lymph_number第2个水平的感兴趣结局事件累积发生率

plot (cum_Lymph_number, color = c ("pink", "red", "blue", "darkcyan", "green", "navy", "purple", "black", rainbow (10)), xlab = "", xlim = c (0,100), ylim = c (0,1), ylab = "CIF", main = '淋巴结检查数量') #绘制生存曲线图
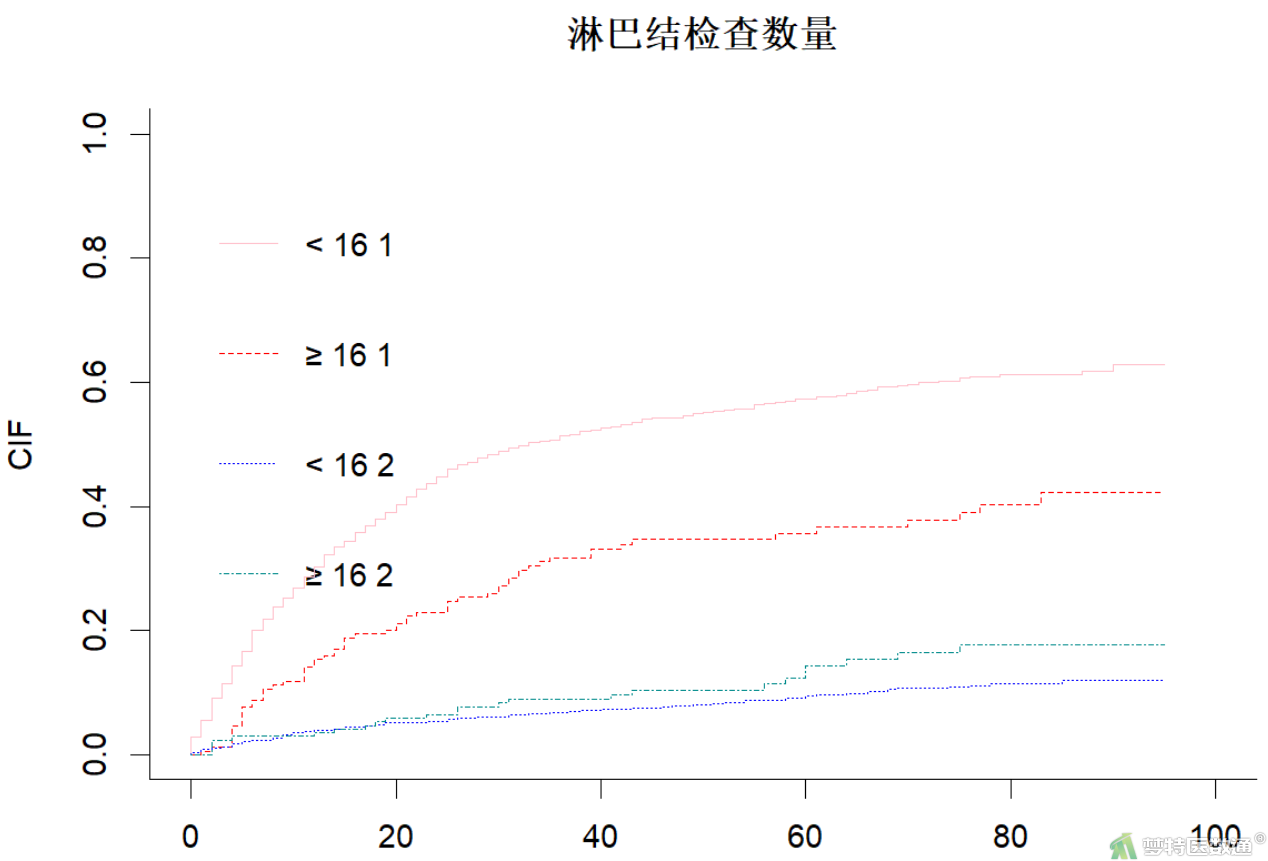
(2) 结果解读
图5结果显示,淋巴结检查数量<16和≥16组中兴趣结局事件的累积发生率分别为62.857%和42.224%。
图4中$est第1、2行分别表示两组不同时间点的兴趣结局事件的累积发生率点估计值,第3、4行分别表示两组不同时间点的竞争风险事件累积发生率点估计值。$Tests第1行表示在控制竞争风险事件后,两组之间兴趣结局事件的累积发生率差异有统计学意义(P=2.680913e-07 <0.001),第2行表示两组之间竞争风险事件累积发生率差异无统计学意义(P=8.427284e-02 >0.05)。$var表示各时间点的方差。
图6为兴趣结局事件累积发生率与竞争风险事件累积发生率的生存曲线,直观表示上述数字化结果。纵坐标表示累积发生率,横坐标是时间轴。从<16 1对应的浅红色曲线和≥16 1对应的深红色虚线曲线可以得出,<16组死于非小细胞肺癌的风险高于≥16组,差异有统计学意义(P=2.680913e-07 <0.001)。从<16 2对应的蓝色虚线曲线和≥16 2对应的绿色虚线曲线可以得出,<16组死于其他原因(竞争事件)的风险低于≥16组,但差异无统计学意义(P=8.427284e-02 >0.05)。即,在控制了竞争风险事件后,<16组死于非小细胞肺癌的风险高于≥16组,差异有统计学意义(P=2.680913e-07 <0.001)。
3. 单因素竞争风险回归分析
(1) 软件操作
fgr_Lymph_number <- FGR(Hist(Survival_months, Outcome)~ Lymph_number, data = mydata) #淋巴结检查数量的单因素竞争风险回归分析 summary (fgr_Lymph_number) #查看分析结果

fgr_Age <- FGR(Hist(Survival_months, Outcome)~ Age, data = mydata) #年龄的单因素竞争风险回归分析 summary (fgr_Age) #查看分析结果
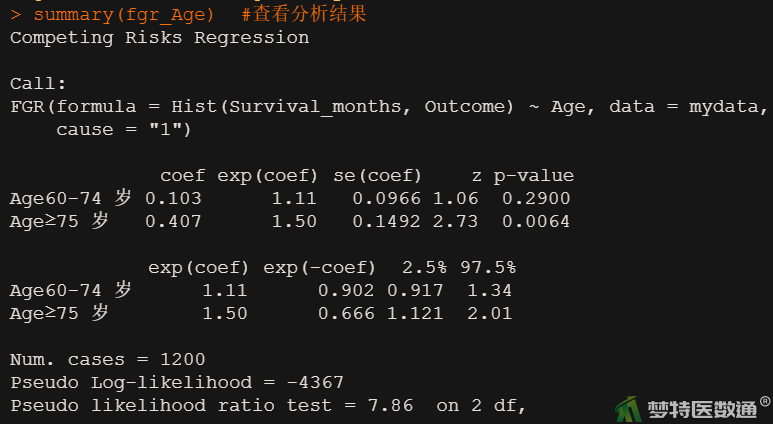
fgr_Gender <- FGR(Hist(Survival_months, Outcome)~ Gender, data = mydata) #性别的单因素竞争风险回归分析 summary (fgr_Gender) #查看分析结果

fgr_Ethnicity <- FGR(Hist(Survival_months, Outcome)~ Ethnicity, data = mydata) #种族的单因素竞争风险回归分析 summary (fgr_Ethnicity) #查看分析结果
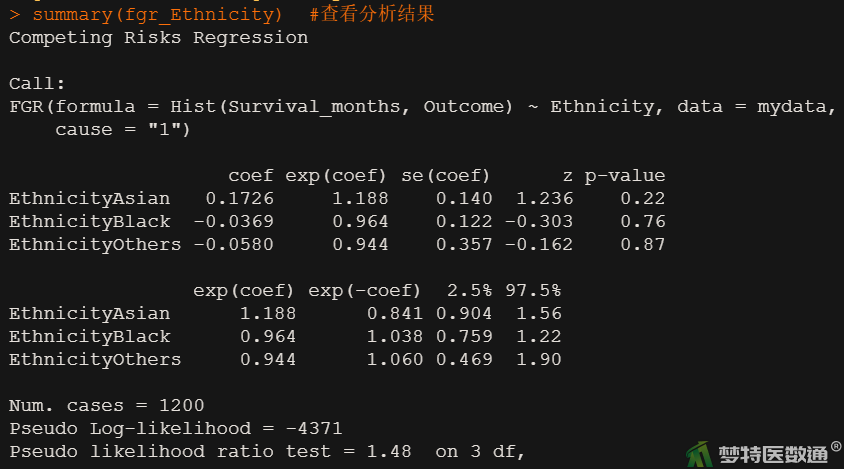
fgr_Primary_site <- FGR(Hist(Survival_months, Outcome)~Primary_site, data = mydata) #原位癌病发部位的单因素竞争风险回归分析 summary (fgr_Primary_site) #查看分析结果

fgr_T_stage <- FGR(Hist(Survival_months, Outcome)~T_stage, data = mydata) #T分期的单因素竞争风险回归分析 summary (fgr_T_stage ) #查看分析结果
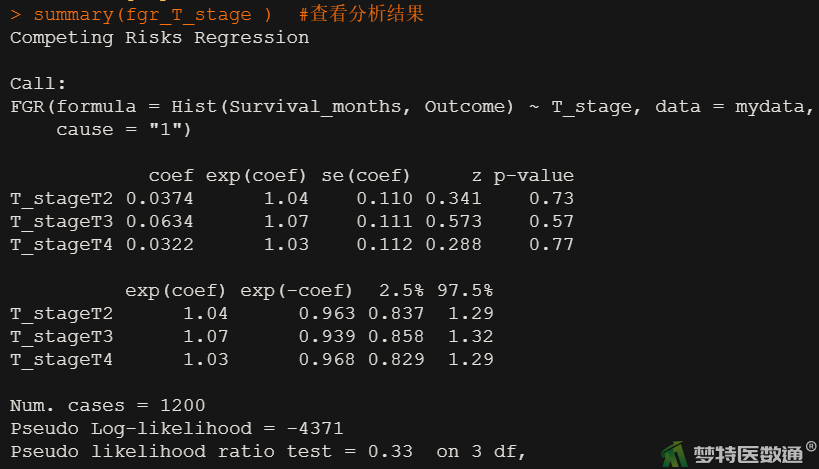
(2) 结果解读
图7为淋巴结检查数量的单因素竞争风险回归分析结果,显示在控制了竞争风险事件后,<16组死于非小细胞肺癌的风险比≥16组高0.91倍 (HR=1.91),或≥16组死于非小细胞肺癌的风险比<16组低0.477倍 (HR=0.523, 95%CI: 0.407-0.673)。
同理,根据图8-图11结果可解读其他变量的回归分析结果,可知如果取检验水准为0.1,则年龄、性别、原位癌病发部位三个自变量分析结果有统计学意义,可被纳入后续多因素竞争风险回归分析进行校正;种族、T分期分析结果无统计学意义,可不被纳入。
4.多因素竞赛风险回归分析
(1) 软件操作
根据单因素回归分析对变量进行筛选后,将“Age”、“Gender”、“Primary_site”、“Lymph_number”等变量全部纳入多因素Fine-Gray模型分析。
fgr_multi <- FGR (Hist(Survival_months, Outcome)~Age + Gender + Primary_site + Lymph_number, data = mydata) #多因素竞争风险回归分析 summary (fgr_multi) #查看分析结果

(2) 结果解读
多因素竞争风险回归分析结果显示,在控制了竞争风险事件后,淋巴结检查数量<16组死于非小细胞肺癌的风险比≥16组高0.908倍 (HR=1.908),或≥16组死于非小细胞肺癌的风险比<16组低0.476倍 (HR=0.524, 95%CI: 0.407-0.674)。
其他自变量为协变量,其分析结果可不必关注。
5. 适用条件判断
(1) 子分布满足PH假定
(a) 软件操作
library ('survival') #加载survival包
library ('survminer') #加载survminer包
data_1 <- mydata[mydata$Outcome!=2,] #筛选兴趣事件的数据
data_2 <- mydata[mydata$Outcome!=1,] #筛选竞争事件的数据
data_2$Outcome <- ifelse(data_2$Outcome ==0,0,1) #将data_2中outcome数据重新编码为0和1,即将0编码为0,2编码为1
cox_1 <- coxph (formula = Surv(Survival_months, Outcome) ~ Age + Gender + Primary_site + Lymph_number, data = data_1, id = ID) #拟合data_1的Cox回归模型
cox_2 <- coxph (formula = Surv(Survival_months, Outcome) ~ Age + Gender + Primary_site + Lymph_number, data = data_2, id = ID) #拟合data_2的Cox回归模型
ph_1 <- cox.zph(cox_1) # cox_1的PH检验
ph_2 <- cox.zph(cox_2) # cox_2的PH检验
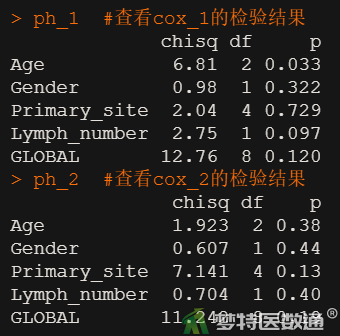
ph_1 #查看cox_1的检验结果
ph_2 #查看cox_2的检验结果
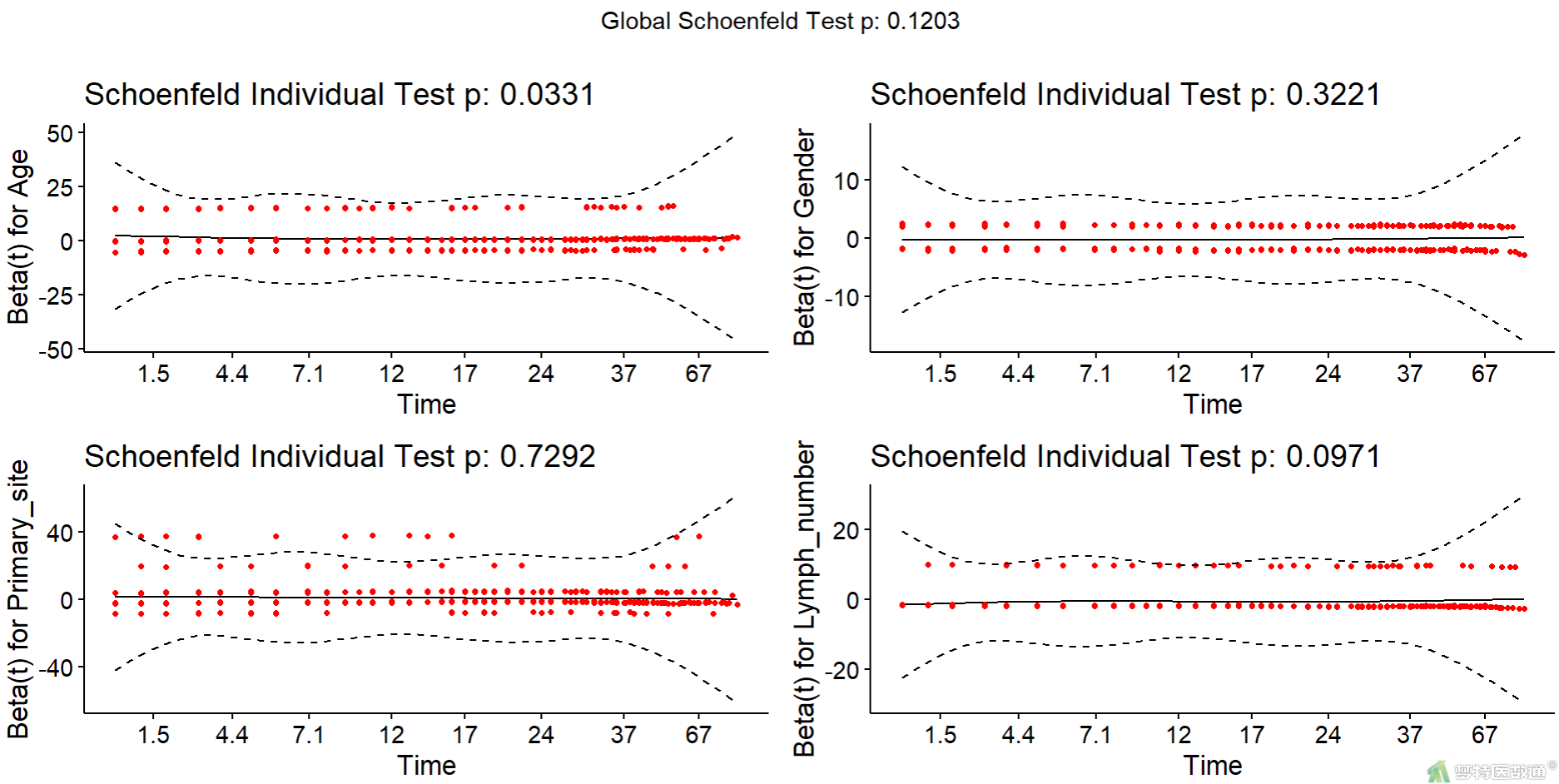
ggcoxzph (ph_1) #绘制cox_1的残差图
ggcoxzph(ph_2) #绘制cox_2的残差图
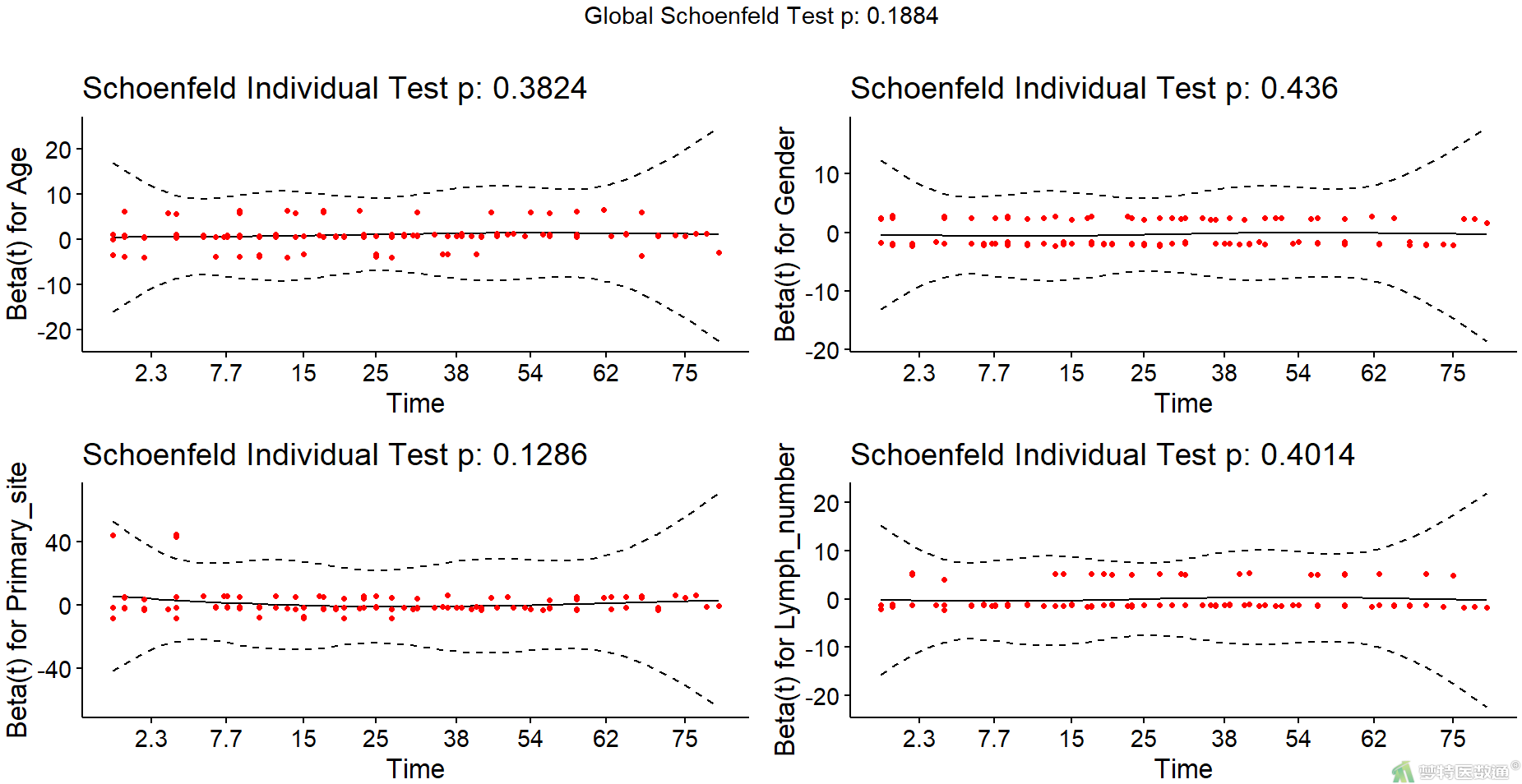
(b) 结果解读
由图14检验结果及残差图可知,协变量Age在模型1中的检验P值为0.033,表明不满足等比例风险假设。但鉴于两个模型的整体检验P值分别为0.120和0.188,均>0.05,且目标自变量(淋巴结检查数量)的检验P值均>0.05,可认为分析模型满足PH假设。
(2) 多重共线性
(a) 软件操作
library ('car') #加载car包
data_lm <- mydata #copy数据
data_lm$Group <- 1:length(data_lm[,1]) #创建因变量
lm_model <- lm (formula = Group ~ Age + Gender + Primary_site + Lymph_number, data = data_lm) #线性模型拟合
vif(lm_model) #计算vif值

(b) 结果解读
图17为多重共线性考察结果,显示各协变量方差膨胀因子VIF均<10,提示模型中无严重多重共线性存在。
四、总结
本研究目的为基于竞争风险模型下,探索淋巴结检查数量与非小细胞肺癌患者生存时间的关系。组别累积发生率分析发现,淋巴结检查数量<16和≥16组中兴趣结局事件的累积发生率分别为62.857%和42.224%。单因素竞争风险回归分析结果,显示在控制了竞争风险事件后,≥16组死于非小细胞肺癌的风险比<16组低0.477倍 (HR=0.523, 95%CI: 0.407-0.673)。根据单因素回归分析结果,对“Age”、“Gender”、“Primary_site”三个协变量纳入多因素Fine-Gray模型分析,结果显示在控制了竞争风险事件后,淋巴结检查数量≥16组死于非小细胞肺癌的风险比<16组低0.476倍 (HR=0.524, 95%CI: 0.407-0.674)。模型满足PH假定,无严重多重共线性存在。
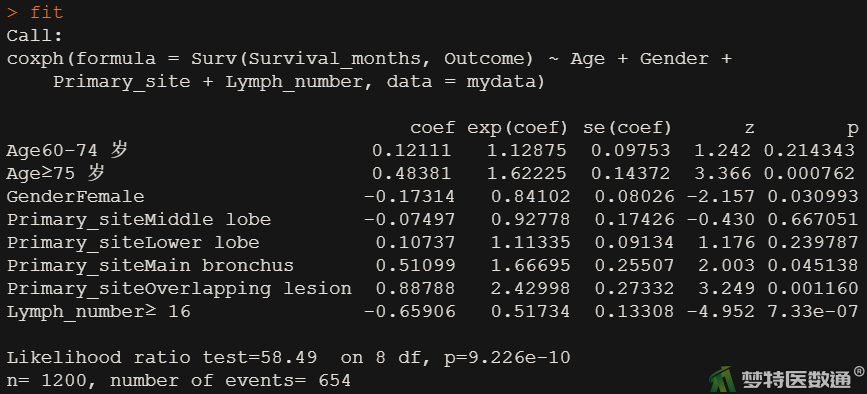
五、知识小贴士
本例如果不考虑竞争风险事件,将其他原因导致的死亡事件作为删失处理,在校正同样协变量情况下,使用传统多因素等比例风险Cox回归分析结果如图18所示。可得,淋巴结检查数量≥16组死于非小细胞肺癌的风险比<16组低0.483倍 (HR=0.517, P=7.33e-07<0.001)。可见在存在竞争风险时,若不使用竞争风险模型,而使用传统等比例风险Cox回归,将会夸大研究因素的效应。