前面文章介绍了“泊松分布(Poisson Distribution)——理论介绍”, 提到Possion分布是一种描述和分析稀有事件发生次数的概率分析方法。泊松分布是偏态分布,线性回归不能解决相关问题,一般推荐使用Poisson回归(Poisson Regression)。Poisson回归主要用于分析服从Poisson分布的因变量与影响其取值的自变量之间变化关系的一种模型,即单位时间(或空间)内某稀有事件发生数的影响因素分析,如某罕见疾病的发病率的影响因素分析。医学研究中有不少现象可使用泊松回归进行分析,比如对浅表性胃炎病人长期随访一段时间后的胃癌发生数。
关键词:泊松回归; Poisson回归; 等离散
一、基本概念
若因变量Y是一个服从均数为𝜆的Poisson分布的随机变量,影响𝜆取值的m个因素为X1, X2, X3, …,Xm。在广义线性模型中,对服从Poisson分布的因变量,连接函数一般取自然对数,即:
\(\ln (\lambda)=\beta_{0}+\beta_{1} X_{1}+\beta_{2}X_{2}+\cdots+\beta_{m} X_{m}\)
\(\lambda=\exp ^{\left(\beta_{0}+\beta_{1}X_{1}+\beta_{2} X_{2}+\cdots+\beta_{m}X_{m}\right)}\)
该模型中假设各因素对事件数的影响是指数相乘的,故称为Poisson乘法模型。β0为截距,βm为回归系数,其意义为:在其他变量不变的情况下,自变量Xm每改变一个单位所引起平均事件发生数之对数的改变量。将回归系数βj转化为相对危险度或发病率比值(incident rate ratio,IRR)的估计值,其结果容易解释:
\(\widehat{R R}=\widehat{R R}=\exp^{\left(b_{m}\right)}=\frac{\lambda_{m1}}{\lambda_{m 0}}\)
当不同观察单位的发生事件观测基数不一样时,需要将发生数除以相应单位的总观测数,用于抵消观察单位数的不同对结果造成的影响,其表达式为:
\(\ln \left(\widehat{y}_{l}\right)=\ln\left(n_{i}\right)+\beta_{0}+\beta_{1} X_{i1}+\beta_{2} X_{i 2}+\cdots+\beta_{m} X_{i m}\)
其中ln(ni)称为偏移量(offset);该模型可用于个体层次的数据,i指个体;也可以用于分组数据,i指列联表中的一个单元格。
Poisson乘法模型使得自变量的线性预测区间恒大于0,即保证了平均事件的估计值为正值。通常用Newton-Raphson迭代法求参数的极大似然估计值。
二、适用条件
考察一组资料是否可以采用Poisson回归进行分析,至少需要满足以下2个条件:
条件1:一个事件的发生不影响其它事件的发生,即事件独立发生,不存在传染性、聚集性的事件。
条件2:因变量Y服从Poisson分布,总体均数𝜆 =总体方差σ²。
三、参数估计与假设检验
(一) 参数估计
一般采用极大似然法估计参数,即选择有最大概率获得当前样本的值作为参数的估计值,相关似然函数的公式如下:
\(L=\frac{\prod_{i=1}^{n}\left[\exp\left(\sum_{j=0}^{m} \beta_{j} x_{i j}\right)\right]^{y_{i}} \times \exp \left[-\exp\left(\sum_{j=0}^{m} \beta_{j} x_{i j}\right)\right]}{\prod_{i=1}^{n} y_{i}}\)
式中,\(y_{i}\)为第i个观察单位的实际事件发生数。将上面的公式两边取自然对数,就lnL分别对β0,β1,…,βm求偏导数,并令其等于0,得到i+1个方程,采用迭代法解此方程组,即得到β0,β1,…,βm的估计值b0,b1,…,bm。
(二) 回归系数的假设检验
参数的假设检验常用似然比检验或者Wald检验,其计算方法与逻辑回归等广义线性模型相同。
1. 似然比检验(likelihood ratio test)
比较两个相嵌套模型(比如模型A嵌套于模型B内)的对数似然函数统计量LR,其计算公式为:
\(L R=-2\left(\ln _{A}-\ln _{B}\right)\)
其中lnA为模型A的对数似然函数值,lnB为模型B的对数似然函数值。似然比统计量近似服从χ2分布,自由度df为模型A和模型B自变量数的差值,根据χ2值和相应的自由度可计算出P值。当P≤0.05时,拒绝零假设,意味着纳入的变量对模型来说有统计学意义。
2. Wald检验
Wald检验只需将各参数βi的估计值bi与0比较,并用它的标准误作为参照;为检验H0:βi=0,H1:βi≠0,计算如下统计量,其检验假设为:
\(\text { Wald } \chi2=\left[\frac{\widehat{\beta}_{J}-0}{SE\left(\widehat{\beta}_{J}\right)}\right]^{2}\)
Wald χ2值服从χ2分布,根据χ2值和相应的自由度可计算出P值。当P≤0.05时,拒绝零假设,意味着纳入的变量对模型来说有统计学意义。
(三) 拟合优度检验
对Poisson回归的拟合优度检验,常用Pearson χ2统计量、尺度χ2统计量(Scaled Pearson) 或残差偏移量(deviance)、尺度残差偏移量(Scaled deviance),相关公式如下:
\(\text { Pearson } \chi^{2}=\sum_{1}^{i} \frac{w_{i}\left(y_{i}-\mu_{i}\right)}{V\left(\mu_{i}\right)}\)
\(\text { Scaled Pearson } \chi^{2}=\sum_{1}^{i} \frac{w_{i}\left(y_{i}-\mu_{i}\right)}{V\left(\mu_{i}\right)}, \emptyset=\chi^{2} /(m-p)\)
\(\operatorname{Deviance}(D)=2 \sum_{1}^{i} w_{i}\left[y_{i} \ln \left(\frac{y_{i}}{\mu_{i}}\right)-\left(y_{i}-\mu_{i}\right)\right]\)
\(\text { Scaled Deviance }(D)=\frac{2 \sum_{1}^{i} w_{i}\left[y_{i} \ln \left(\frac{y_{i}}{\mu_{i}}\right)-\left(y_{i}-\mu_{i}\right)\right]}{\emptyset}, \emptyset=D /(m-p)\)
其中,yi表示不同自变量水平下的观测值,µi表示期望数,V(µi)表示方差,wi为相同观察单位值重复的个数,\(\varnothing\)表示离散程度,m为观察值的个数,p为模型中拟合参数的个数。当p>0.05时,可认为该数据拟合相应的Poisson回归模型是合适的,当p≤0.05时,选用Poisson回归模型分析该数据是不合适的。
此外还有利用其他模型适配指标进行比较,包括AIC、BIC等评价指标,这些指标值均为值越小,说明模型对数据的适配度越好。
四、案例分析
某临床医师对39名有胸闷症状的非器质性心脏病男性患者的24小时早搏数进行了临床研究记录,每个患者的研究影响因素包括变量X1是否喝浓茶(0为不喝浓茶,1为喝浓茶)、变量X2是否吸烟(0为不吸烟,1为吸烟)。请利用该资料对24小时早搏数的影响因素进行分析。数据见图1。
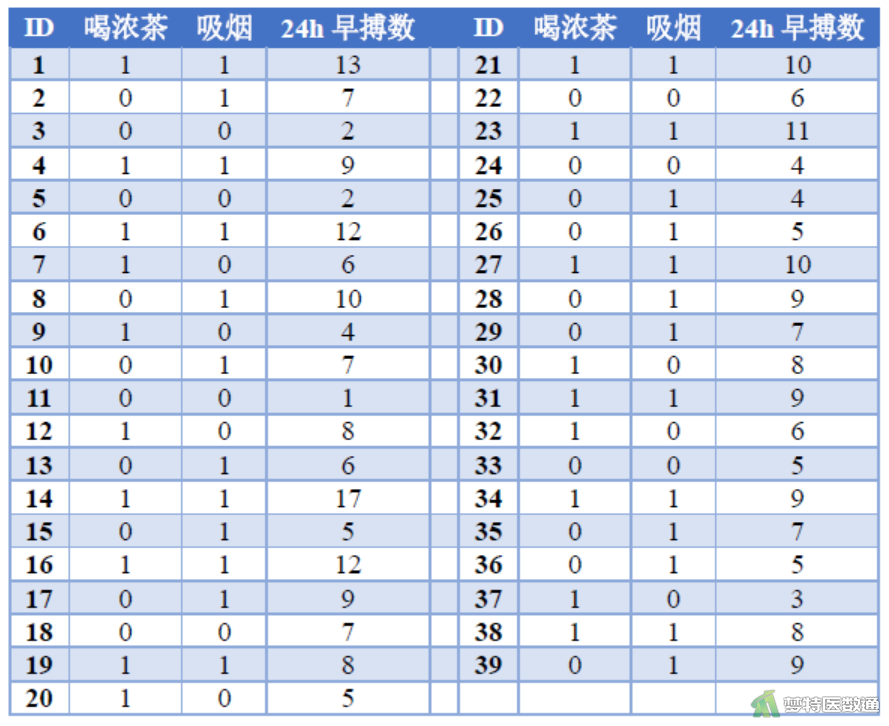
(一) 参数估计
通过统计分析软件可得到模型的截距、每个自变量对应的回归系数(β)及其标准误,exp(β)及其95%的置信区间,详见图2。

据此可得出模型的表达式为:
Ln(Y)=1.848+0.423X1+0.608X2
(二) 似然比检验
首先计算出模型中同时包含“是否喝浓茶”和“是否喝吸烟”变量的对数似然函数值ln(X1, X2),再分别计算出模型中不包含“是否喝浓茶”的对数似然函数值ln(X1)和不包含“是否喝吸烟”的对数似然函数值ln(X2)。根据案例可得ln(X1, X2) = -85.383,ln(X1) = -91.667,ln(X2) = -95.835。
1. 对“是否喝浓茶”变量回归系数的似然比检验
(1) 建立检验假设,确定检验水准
H0:β1=0
H1:β1≠0
α=0.05
(2) 计算统计量
LR = -2[ln(X1)- ln(X1, X2)] = -2×[-91.667-(-85.383)]=12.568
(3) 确定P值,作出推断结论
自由度υ=1,查(χ2界值表)得P<0.005,按α=0.05水准,拒绝H0,接受H1,可认为“是否喝浓茶”与24小时早搏数有显著性关系。
2. 对“是否吸烟”变量回归系数的似然比检验
(1) 建立检验假设,确定检验水准
H0:β2=0
H1:β2≠0
α=0.05
(2) 计算统计量
LR=-2[ln(X2)- ln(X1, X2)]=-2×[-95.835-(-85.383)]=20.905
(3) 确定P值,作出推断结论
自由度υ=1,查(χ2界值表)得P<0.005,按α=0.05水准,拒绝H0,接受H1,可认为“是否吸烟”与24小时早搏数有显著性关系。
(三) Wald检验
1. 对“是否喝浓茶”变量回归系数的Wald检验
(1) 建立检验假设,确定检验水准
H0:β1=0
H1:β1≠0
α=0.05
(2) 计算统计量
\(\text { Wald } \chi 2=\left[\frac{\widehat{\beta_{1}}-0}{S E\left(\widehat{\beta_{1}}\right)}\right]^{2}=\left[\frac{0.608-0}{0.140}\right]^{2}=18.860\)
(3) 确定P值,作出推断结论
自由度υ=1,查(χ2界值表)得P<0.005,按α=0.05水准,拒绝H0,接受H1,可认为“是否喝浓茶”与24小时早搏数有显著性关系。
2. 对“是否喝吸烟”变量回归系数的Wald检验
(1) 建立检验假设,确定检验水准
H0:β2=0
H1:β2≠0
α=0.05
(2) 计算统计量
\(\text { Wald } \chi 2=\left[\frac{\widehat{\beta_{2}}-0}{S E\left(\widehat{\beta_{2}}\right)}\right]^{2}=\left[\frac{0.423-0}{0.120}\right]^{2}=12.426\)
(3) 确定P值,作出推断结论
自由度υ=1,查(χ2界值表)得P<0.005,按α=0.05水准,拒绝H0,接受H1,可认为“是否吸烟”与24小时早搏数有显著性关系。
(四) 拟合优度检验
由相应软件可计算出Pearsonχ2、deviance、AIC、BIC等拟合优度检验指标,AIC=176.765,BIC=181.752,其中deviance=25.112,相应的自由度ν=36,相应的P值=0.913>0.05,表明用Poisson回归模型分析该资料是合适的。