在前面文章中介绍了Cox比例风险回归模型(Cox Proportional Hazard Regression Model),本篇文章将实例演示在SPSS软件中实现时间依存Cox回归模型的操作步骤。
关键词:SPSS; Cox等比例回归; Cox回归; 生存分析; 等比例风险; 含时间依存协变量; 时依协变量
一、案例介绍
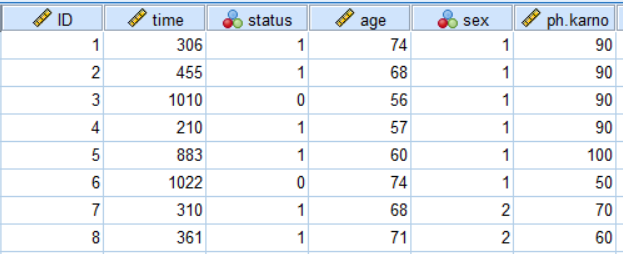
某肿瘤研究所收集了200例肺癌患者的生存数据:包括生存状态(status,0=“删失”,1=“死亡”)、生存时间(time,天)、性别(sex,1=“男”,2=“女”)、年龄 (age,岁)和卡氏评分(ph.karno),部分数据见图1。现欲探究患者的性别、年龄、卡氏评分与生存结局的关系。本文案例可从“附件下载”处下载。
二、问题分析
本案例的目的是探究肺癌患者的性别、年龄和卡氏评分与生存结局的关系,可以采用Cox比例风险回归模型进行分析,但需要满足5个条件:
条件1:因变量是含有时间信息的二分类变量。本案例中因变量是包含生存时间的二分类资料,time是生存时间(天);status是生存结局。本案例数据满足该条件。
条件2:各观测值之间相互独立,无互相干扰。由数据和研究设计可知,该条件满足。
条件3:一般要求结局事件的样本量为自变量个数的10~20倍(EPV原则)。该条件需要软件分析来判断。
条件4:自变量之间无严重多重共线性。该条件需要软件分析来判断。
条件5:等比例风险(Proportional hazards,PH)假设,该条件需要软件分析来判断。
三、软件操作及结果解读
(一) 适用条件判断
1. 条件3判断
(1) 软件操作
① 选择“分析”—“描述统计”—频率”(图2)。
② 在“频率”对话框中将变量“status”选入右侧“变量”框中,点击“确定”(图3)。
(2) 结果解读
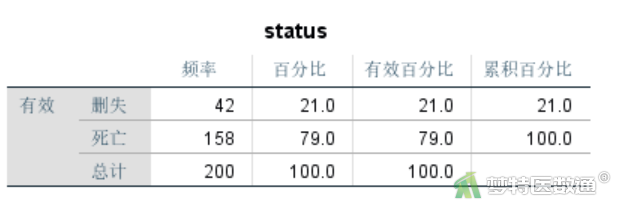
由图4结果可知因变量中结局事件为158例。按照EPV为10~20的原则可满足多因素模型纳入7~15个变量的需求。因此,本案例数据满足条件3。
2. 条件4判断 (共线性检测)
(1) 软件操作
① 点击“分析”→“回归”→“线性”(图5)。
② 将变量“status”选入“因变量”,变量“age”、”sex”和“ph.kamo”选入“自变量”(图6)。
③ 点击“统计”,在“统计”子对话框中勾选“共线性诊断”(图7),点击“继续”后回到主对话框,点击“确定”。
(2) 结果解读
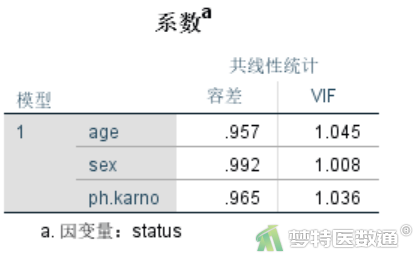
如果“Tolerance(容忍度)”小于0.1或“VIF(方差膨胀因子)”大于10,则提示有严重共线性存在。本例中(图8),各变量的容忍度均远大于0.1,方差膨胀因子均远小于10,提示自变量之间不存在严重多重共线性。如果数据存在严重多重共线性,需用复杂的方法进行处理,其中最简单的是剔除引起共线性的因素之一,剔除哪一个因素可以基于理论依据。满足条件4。
3. 条件5判断 (等比例风险判定)
PH假定指自变量对生存率[风险比值h(t)/h0(t)]的影响不会随时间的变化而变化。若不满足PH假定,则需要改用含时间依存协变量的Cox比例模型分析数据。本案例PH假定的检验详见本章后文。
(二) 统计描述及推断
1. 统计描述
(1) 软件操作
① 选择“分析”—“描述统计”—“频率”(图9)。
② 在“频率 ”对话框中将变量“sex”选入右侧“变量”框中,点击“确定”(图10)。
③ 选择“分析”—“描述统计”—“描述”(图11)。
④ 在“描述 ”对话框中将变量“time”、“age”和“ph.karno”选入右侧“变量”框中,点击“确定”(图12)。

(2) 结果解读
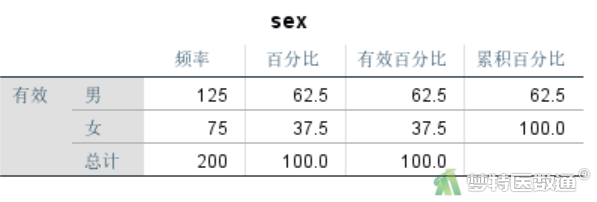
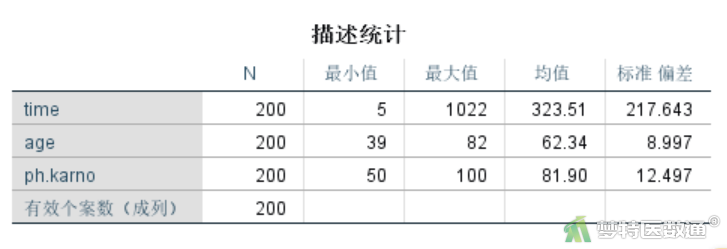
如图13、图14和图4所示,本研究共纳入200例肺癌患者,其中男性125例(62.50%),女性75例(37.50%);所有研究对象的平均生存时间为323.51天,随访过程中158例(79.00%)死亡;所有研究对象的年龄为(62.34±8.997)岁,卡氏评分为(81.90±12.497)分。
2. 单因素分析
(1) 软件操作
① 选择“分析”—“生存分析”—“Cox回归”(图15),将 “time”选入“时间”,将“status”选入“状态”, 将“age”选入“协变量” (图16)。

② 点击“定义事件”,在“单值”填入“1”, 点击“继续”后回到主对话框(图17)。
③ 点击“选项”,勾选“Exp(B)的置信区间”(图18),点击“继续”后回到主对话框,点击“确定”。

④ 按照以上步骤对“sex”、“ph.karno”分别进行单因素分析。
(2) 结果解读
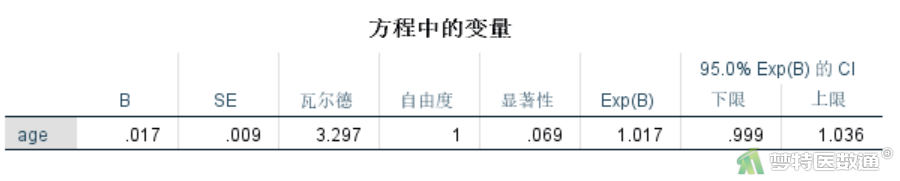
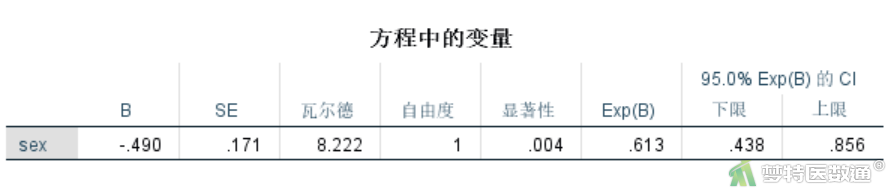
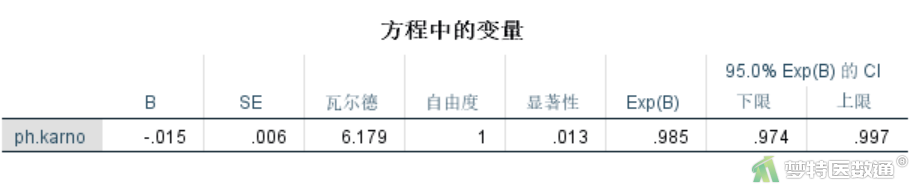
单因素Cox比例风险模型分析显示(图19—图21),年龄、性别和卡氏评分与生存结局之间均存在统计学关联(P<0.1),年龄每增加一岁肺癌患者的死亡风险增加1.7% (HR=1.017,95%CI:0.999~1.036;P=0.069);女性死亡风险比男性低38.7% (HR=0.613,95%CI:0.438~0.856;P=0.004);卡氏评分每上升一个单位肺癌患者死亡的风险下降1.5% (HR=0.985,95%CI:0.974~0.997;P=0.013)。
3. 条件5判断 (等比例风险判定)
将单因素Cox比例风险模型分析中有统计学关联的变量(年龄、性别、卡氏评分)纳入到多因素Cox比例风险模型。
(1) 软件操作
① 选择“分析”—“生存分析”—“Cox回归”(图15),将 “time”选入“时间”,将“status”选入“状态”, 将“age”、“sex”、“ph.karno”选入“协变量” (图22)。

② 点击“定义事件”,在“单值”填入“1”, 点击“继续”后回到主对话框(图17)。
③ 点击“选项”,勾选“Exp(B)的置信区间”(图18),点击“继续”后回到主对话框。
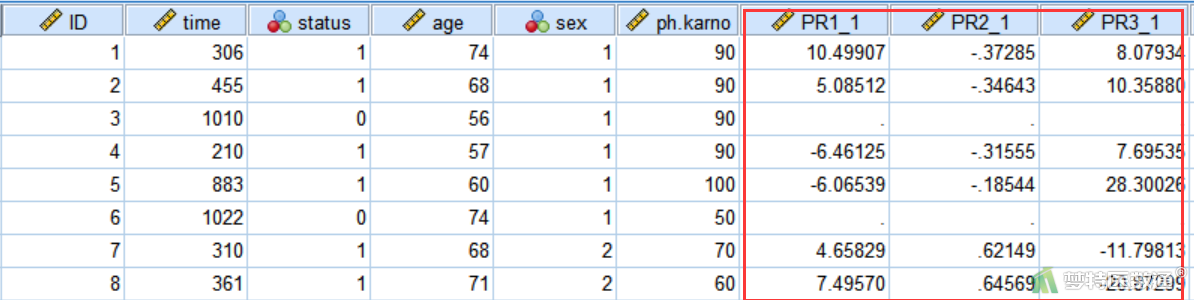
④ 点击“保存”,勾选“偏残差”(图23)。点击“继续”后回到主对话框,点击“确定”。将在数据库中生成三个新变量“PR1_1” “PR2_1” “PR3_1”(图24)。
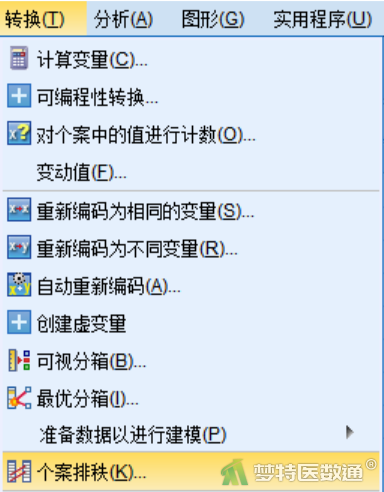
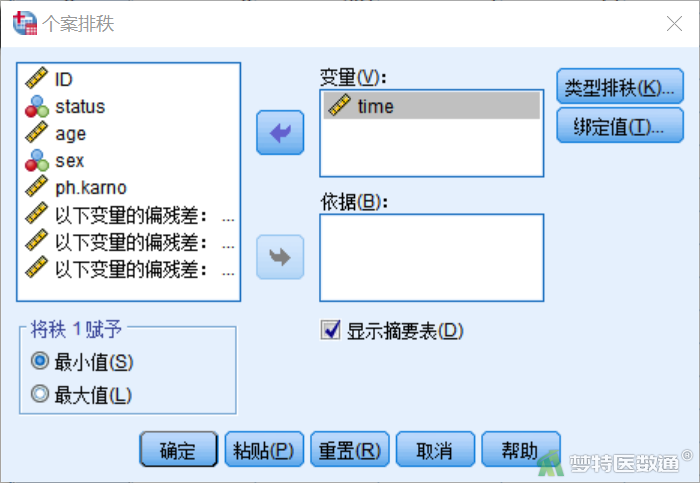
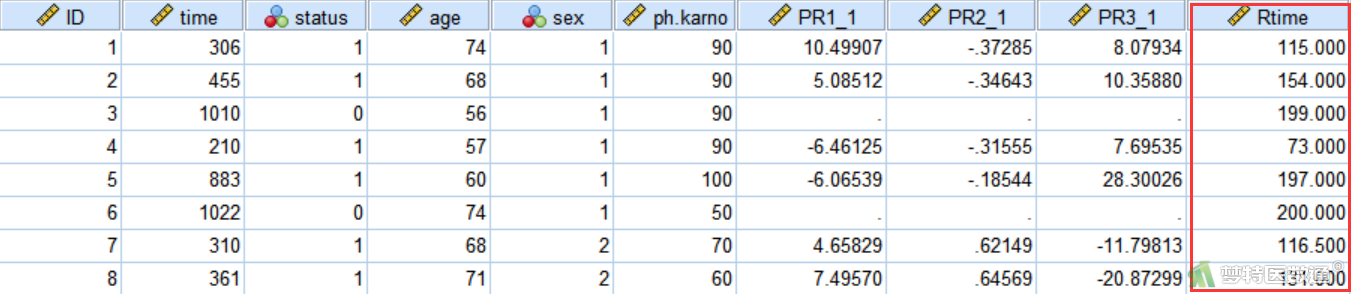
⑤ 选择“转换”—“个案排秩”(图25),将时间变量“time”选入“变量”框中,点击“确定”(图26)。将在数据库中生成一个新变量“Rtime” (图27)。
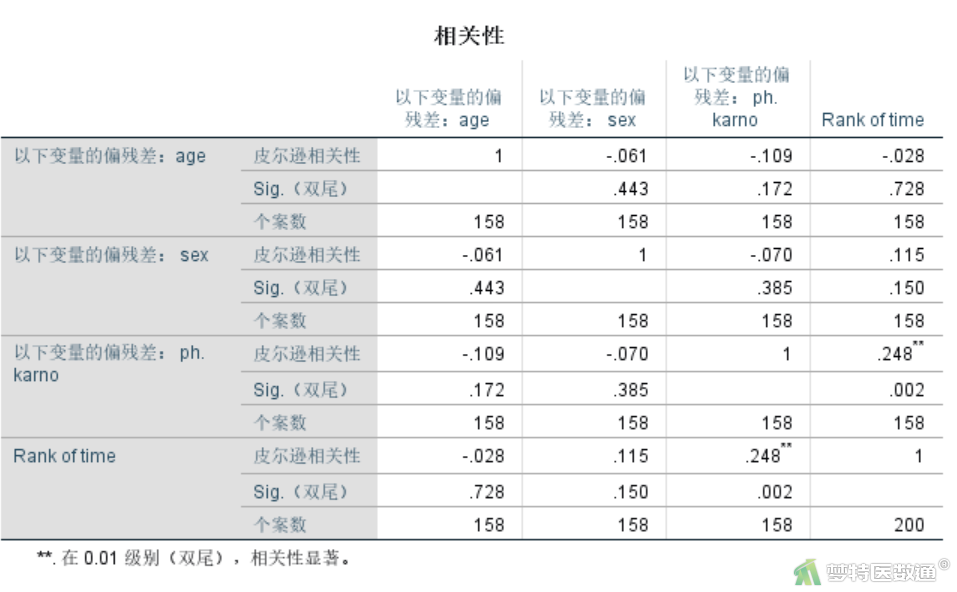
⑥ 选择“分析”—“相关”—“双变量” (图28)。在“双变量相关性”对话框中将变量“Rtime”和“PR1_1”、 “PR2_1” 、“PR3_1”选入右侧“变量”框,选择相关系数中的“皮尔逊”,其他设置保持默认不变,如图29所示,点击“确定”。
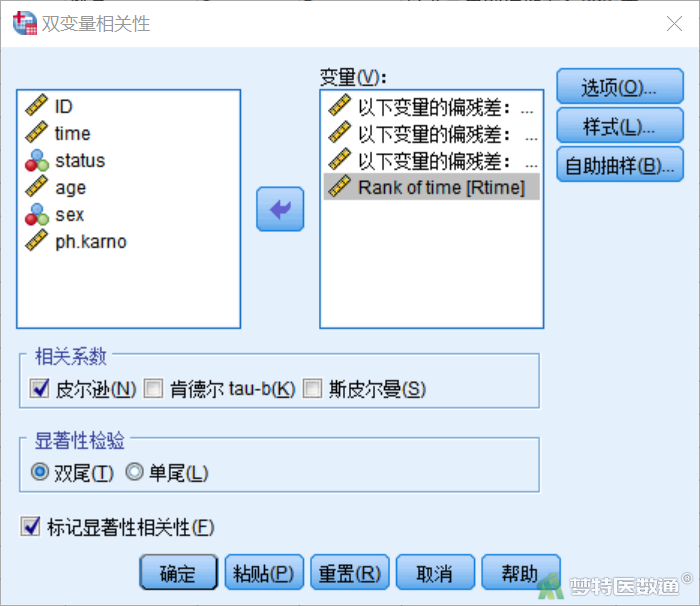
(2) 结果解读
结果显示,“Rtime”与“PR1_1”、“PR2_1”、“PR3_1”的Pearson相关系数分别为-0.028(P=0.728)、0.115(P=0.159)、0.248(P=0.002) (图30),由此提示协变量ph.karno的风险比会随着时间的增加而增加,可认为ph.karno不满足等比例风险假定,不适宜直接进行Cox回归分析。
4. 含时间依存协变量的Cox比例风险模型
由于卡氏评分(phkarno)不满足PH假定,因此需要设立卡氏评分与时间的交互项,与年龄、性别一起建立含时间依存协变量的Cox比例风险模型。
(1) 软件操作
选择“分析”—“生存分析”—“含依时协变量的Cox”(图31),调入公式“LN(T_+20)* ph.karno”(适用于变量是正态/近似正态分布),此时就构建了变量“ph.karno”的依时协变量(图32)。
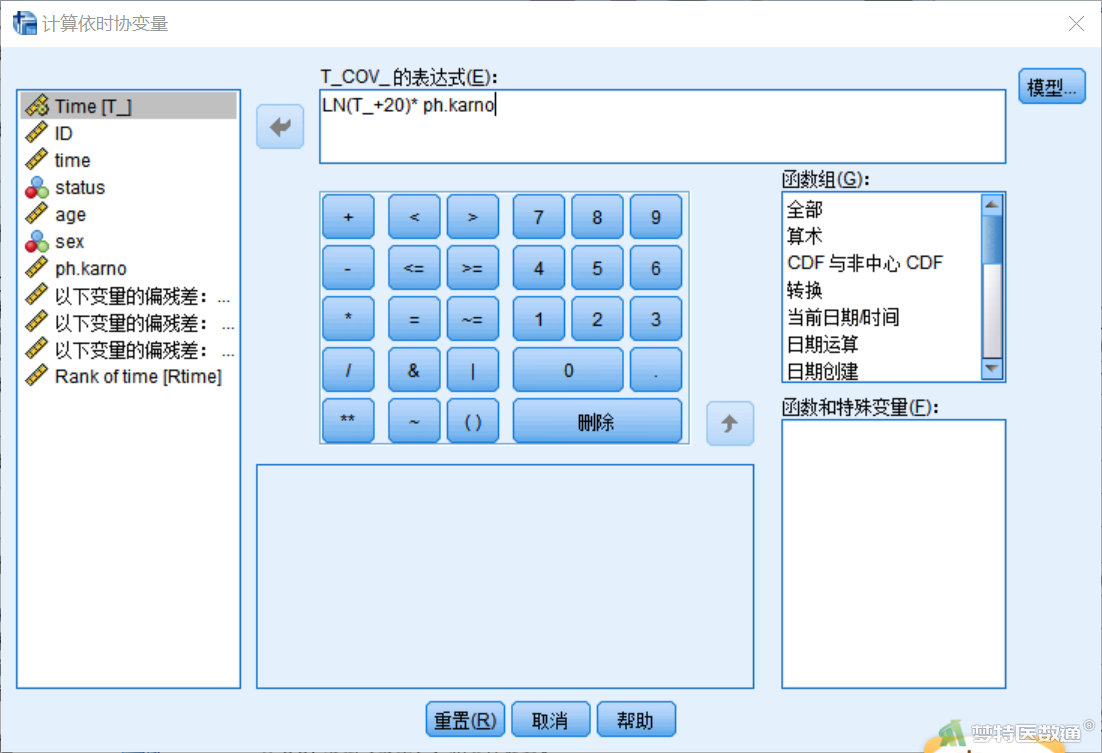
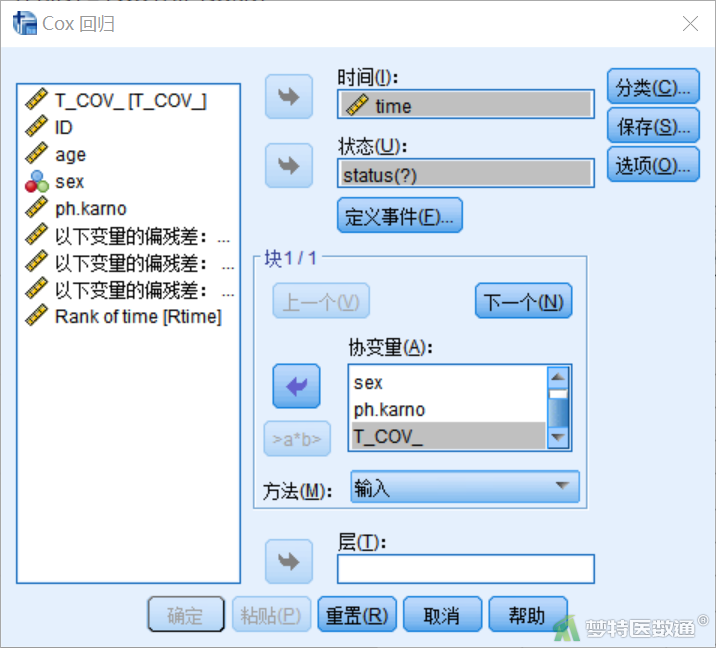
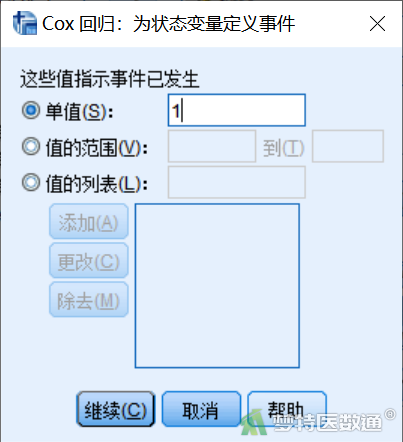
点击图32右上角“模型”,将 “time”选入“时间”,将“status”选入“状态” ,将“age”、“sex”、“ph.karno”、“T_COV_”选入“协变量”(图33)。点击“定义事件”,在“单值”填入“1”, 点击“继续”后回到主对话框(图34)。
点击“选项”,勾选“Exp(B)的置信区间”(图35),点击“继续”后回到主对话框,点击“确定”。
(2) 结果解读
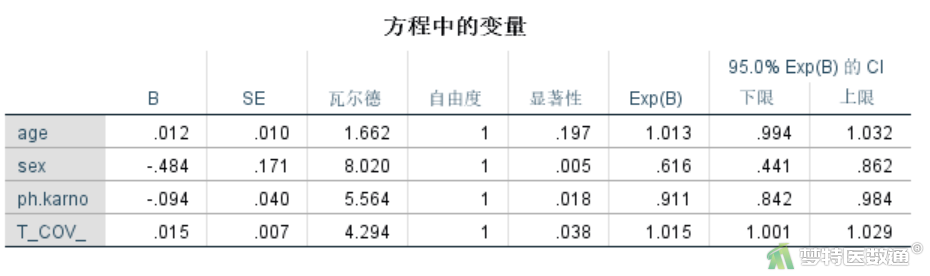
图36分析结果显示,性别的效应值HR为0.616,表示女性死亡的风险比男性低38.4% (HR=0.616,95%CI:0.441~0.861;P=0.005),年龄与生存结局的关联无统计学意义 (HR=1.013,95%CI:0.994~1.032;P=0.197)。卡氏评分的时依系数β(t)= -0.094+0.015×ln(t+20),效应值HR=exp(-0.094+0.015×ln(t+20))。例如,当时间为200天时,卡氏评分对应的HR=exp(-0.094+0.015×ln(200+20))= 0.987。
四、结论
本研究采用Cox比例风险模型探究年龄、性别、卡氏评分与肺癌患者生存结局的关系,数据样本量满足要求,自变量之间无严重多重共线性;PH假定检验发现卡氏评分不满足PH假定,需要建立含时间依存协变量的Cox比例风险模型。
含时间依存协变量的Cox比例风险模型分析结果表明,性别和卡氏评分均是肺癌患者生存结局的影响因素,其中女性死亡的风险比男性低38.4% (HR=0.616,95%CI:0.441~0.861;P=0.005)。年龄与生存结局的关联无统计学意义 (HR=1.013,95%CI:0.994~1.032;P=0.197)。卡氏评分的时依系数β(t)= -0.094+0.015×ln(t+20),效应值HR=exp(-0.094+0.015×ln(t+20))。
五、分析小技巧
- 对于生存数据,如果自变量是分类变量,可以使用Kaplan-Meier生存曲线和log-rank检验进行单因素分析,也可以使用单因素Cox比例风险模型;如果自变量是定量变量,一般单因素分析采用Cox比例风险模型。
- 构建时依协变量时,常选择协变量与时间函数的乘积项。案例中对ln(t)设置为ln(t+20),增加了一个常数,主要作用是使卡氏评分随着时间的死亡风险变化在一段时间范围内呈直线,常数项的大小一般对模型估计结果影响不大。