有序logistic回归分析(Ordinal Logistic Regression Analysis)——SPSS软件实现

关键词：SPSS; 有序logistic回归; 有序逻辑回归; 平行性检验; 比例优势检验

一、案例介绍

在某胃癌筛查项目中，为了确定胃癌筛查的重点人群，研究者想了解首诊“胃癌分期(Stage)”与患者“经济水平(Income)”、“性别(Gender)”和“年龄(Age)”之间的关系，试对数据进行分析。

创建表示胃癌分期的变量“Stage”(1=I-II期、2=III期、3=IV期、4=V期，测量尺度设为“Ordinal(有序分类变量)”；创建表示经济水平的变量“Income”(1=低水平、2=中等水平、3=高水平)，测量尺度设为“Ordinal(有序分类变量)”；创建表示性别的变量“gender”(1=女性、0=男性)，测量尺度设为“Nominal(分类变量)”；创建表示年龄的变量“age”，测量尺度设为“Scale(连续变量)”。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是探讨首诊“胃癌分期”与患者“经济水平”、“性别(Gender)”和“年龄(Age)”之间的关系。在案例中，首诊“胃癌分期”为因变量，有I-II期、III期、IV期、V期4个分类，且分类间有等级次序关系。因此，可以采用有序logistic回归模型进行分析。但需要满足以下5个条件：

条件1：因变量唯一，且为有序多分类变量。本研究中因变量为“胃癌分期”，且为有序多分类变量，该条件满足。

条件2：存在一个或多个自变量。本研究中有三个自变量，“性别”和“经济水平”为分类变量，“年龄”为连续变量，该条件满足。

条件3：观测值相互独立。本研究中各研究对象的观测值都是独立的，不存在互相干扰的情况，该条件满足。

条件4：自变量之间无多重共线性，该条件需要通过软件分析后判断。

条件5：满足平行性，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 哑变量设置

容忍度(Tolerance)或方差膨胀因子(VIF)可以用来诊断自变量之间的多重共线性。SPSS的广义线性模型不能提供这两个指标，可以通过线性回归来获得。进行线性回归的共线性诊断前需要对多分类变量设置哑变量，以下将对多分类变量“Age”进行哑变量设置。

(1) 软件操作

① 点击“转换”—“创建虚变量”(图2)。

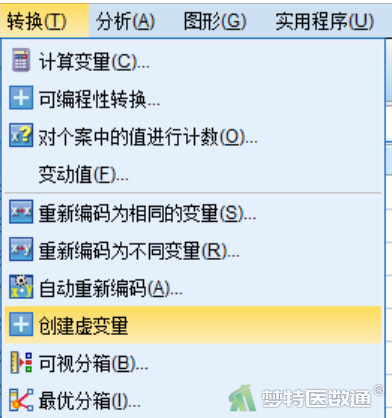
② 在“创建虚变量”对话框中将变量“Income”选入右侧“针对下列变量创建虚变量”框中，然后在“创建主效应虚变量”下的“根名称-每个选定变量各一个”中输入虚拟变量的名称“Income”。点击“确定”，完成虚拟变量设置(图3)。

(2) 结果解读

上述步骤运行结束后可以在数据编辑页面看到新生成的3个哑变量(图4)，随后就可以进行多重共线性诊断。

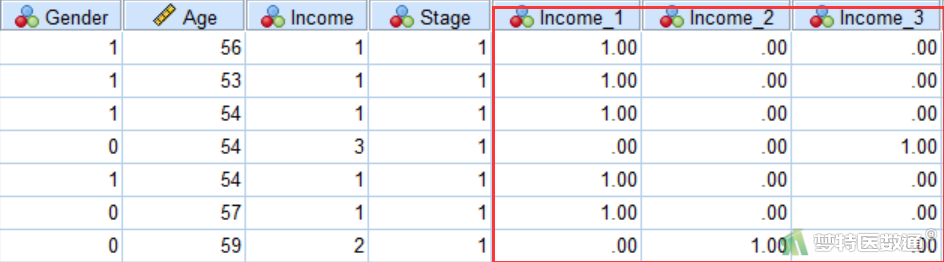
2. 条件4判断(多重共线性诊断)

(1) 软件操作

① 点击“分析”—“回归”—“线性”(图5)。

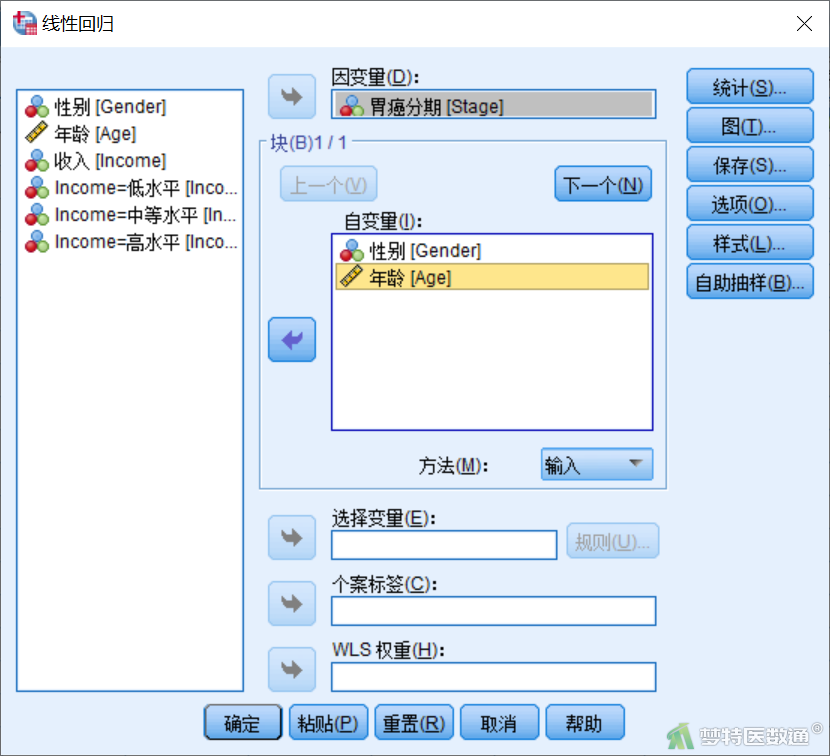
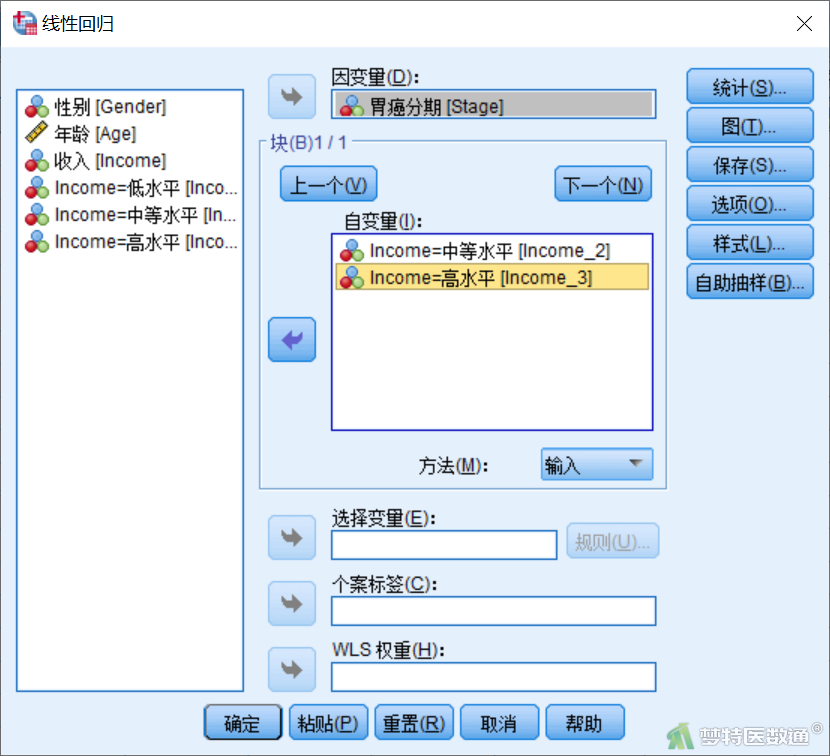
② 将变量“Stage”选入“因变量”，将需要进行多因素分析的变量 “Gender”和“Age”选入“自变量”(图6)，然后点击“下一个”。在图7中将“Income=2”和“Income=3”两个虚拟变量同时选入右侧“自变量”，此即哑变量设置的同进同出原则，此时表示以“Income=1”为参照水平；“方法”选择“输入”。

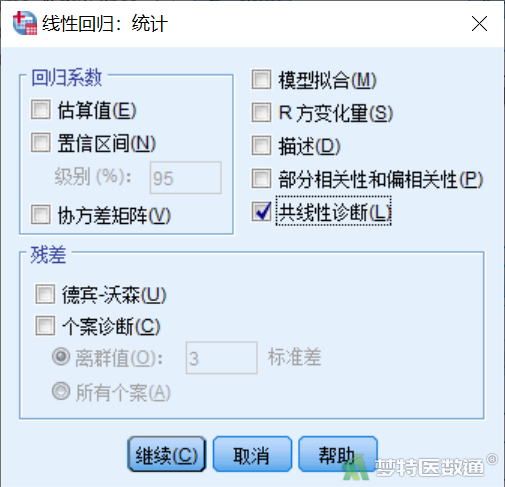
③ 点击“统计”，在“统计”子对话框中勾选“共线性诊断”(图8)，点击“继续”后回到主对话框，点击“确定”。

(2) 结果解读

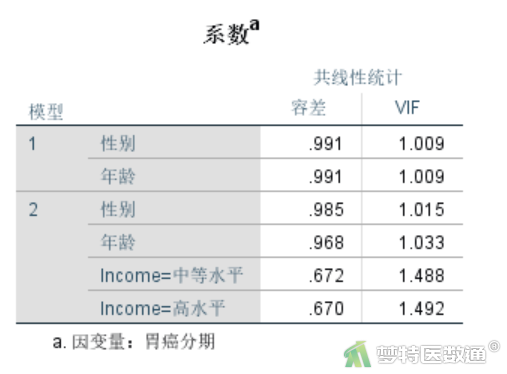
如果“容差”小于0.1或“VIF(方差膨胀因子)”大于10，则提示有严重共线性存在。本例中(图9)，容忍度均远大于0.1，方差膨胀因子均小于10，提示自变量之间不存在严重多重共线性。如果数据存在严重多重共线性，需用复杂的方法进行处理，其中最简单的是剔除引起共线性的因素之一，剔除哪一个因素可以基于理论依据。

3. 条件5判断(平行性检验)

平行性检验的结果可与统计推断结果一起输出，详见下文。

(二) 统计推断

1. 软件操作

① 点击“分析”—“回归”—“有序...”(图10)。

② 在“有序回归”对话框中将变量“Stage”选入“因变量”，将分类变量“Gender”和“Income”选入“因子”。将连续变量“Age”选入“协变量”位置(图11)。

③ 点击右侧“输出”，在输出对话框中选中“平行线检验”，其他选项保持不变，点击“继续”回到主对话框后点击“确定”(图12)。

2. 结果解读

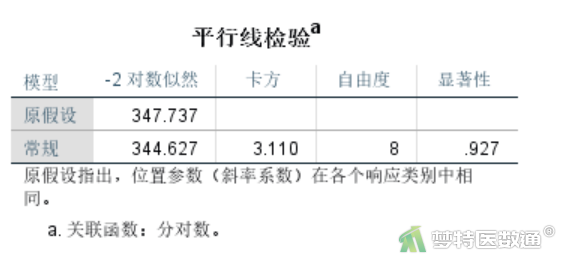
(1) 平行性检验

图13显示了平行线检验结果，χ²= 3.110，P=0.927，说明平行性假设成立，即各回归方程相互平行，故满足条件5，可以使用有序Logistic回归进行分析。

如果平行线假设不能满足，可以考虑以下两种方法进行处理：

① 进行无序多分类Logistic回归，而非有序Logistic回归，此种处理因变量会失去有序的属性；

② 用不同的分割点将因变量变为二分类变量，分别进行二分类Logistic回归。

(2) 模型评价

图14给出的是数据的一般情况，展示了各变量的个案数和所占比例。

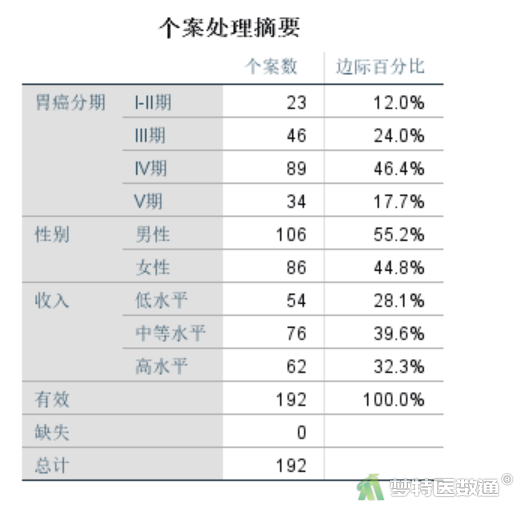
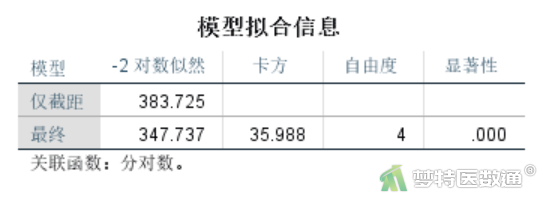
图15“模型拟合信息”是对模型中所有自变量偏回归系数是否均为0进行似然比检验。其中-2对数似然值越小越好，从结果中可以看出，加入自变量后的模型比只有常数项的值更小(347.737<383.725)，模型拟合更好，“Likelihood Ratio Tests(似然比检验)”结果显示模型的改善是有统计学意义的(P<0.001)，即自变量加入是有统计学意义的。

(3) 变量筛选

图16“参数估算值”给出了模型中具体参数的估计值。包括模型中的“回归系数估计值”及其95%CI、“标准错误”、“统计量”、“自由度”、“显著性 (P值)”。

由于因变量有4个水平，共生成4-1=3个模型。“阈值”对应的Stage三个“Estimate(估计值)”分别是本次分析中拆分的三个二分类Logistic回归的常数项。有序多分类Logistic回归假定拆分的多个回归方程中自变量系数均相等(满足平行性假设)，因此“位置”中只给出了一组自变量系数。“Gender”和“Income”对应的“估算”为自变量系数。其中Income为多分类，在分析中被拆分成了三个哑变量(即Income 取值为1、2、3)，以Income=3为对照组。

变量“Income”=1时的系数有统计学意义，所以根据多分类变量同进同出原则，该变量被保留在模型中。变量“Gender”系数无统计学意义(P=0.403)，应该被移除模型。

(4) 拟合优度

在“有序回归”对话框中将变量“Stage”选入“因变量”，将分类变量“Income”选入“因子”。将连续变量“Age”选入“协变量”位置，点击“确定”(图17)，则会再次得到上述模型评价和变量筛选中的结果图，可以得到模型是有统计学意义的(P<0.001)(图18)，即自变量加入是有统计学意义的。

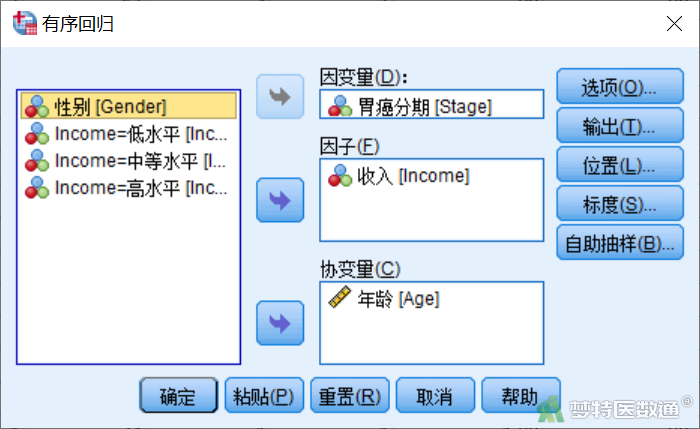
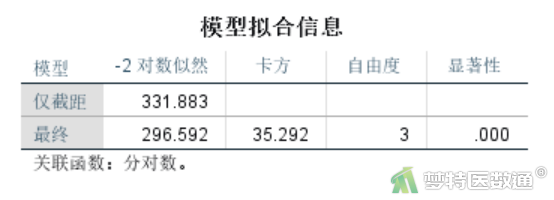
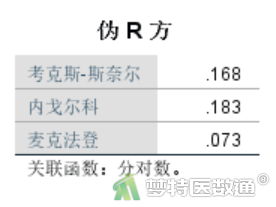
图19是伪R方表，给出了三种伪决定系数：“R²_McF”、“R²_CS”、“R²_N”。均是回归方程对解释变量变异量化的一种反映，越接近1说明回归方程的拟合度越高。对于分类数据的统计分析，一般情况下伪决定系数都不会很高。

(5) 模型系数

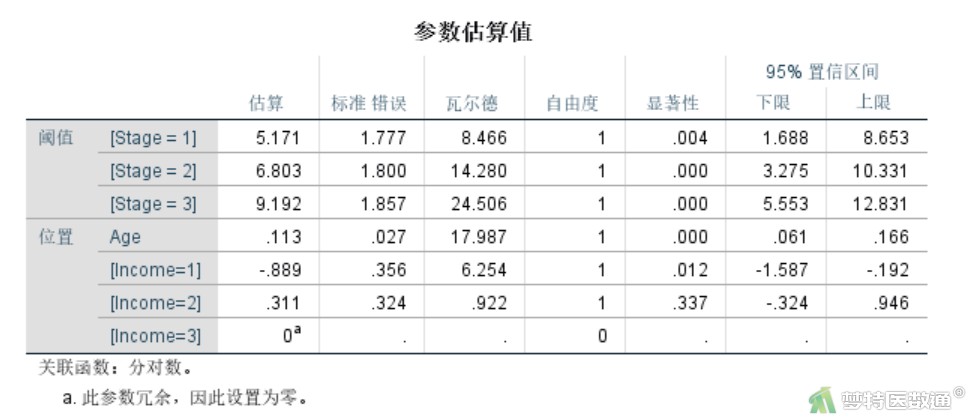
新模型的“参数估算值”结果中显示，年龄每增加一岁，其首诊“胃癌分期”提升一个等级的可能性比原来增加exp(0.113)=1.120倍(95%CI：1.063~1.181，P<0.001)。Income=1时系数“Estimate(估计值)”为-0.889，表示在调整年龄变量的情况下，Income=1(即收入水平最低)的组，相比于Income=3(收入水平最高)的组，首诊胃癌分期高一个等级的可能性是exp(-0.889)=0.411倍(95%CI：0.205~0.825)，P=0.012。Income=2(即收入水平最低)的组，相比于Income=3(收入水平最高)的组，首诊“胃癌分期”差异无统计学意义(P=0.337)。(图20)。

四、结论

本研究采用有序logistic回归模型分析首诊“胃癌分期”与患者“经济水平”、“性别”和“年龄”之间的关系。因变量例数分布满足样本量需求，变量之间不存在严重共线性，满足平行性假设(χ²=3.120，P=0.927)。

“性别”对首诊“胃癌分期”的影响无统计学意义。“年龄”每增加一岁，其首诊“胃癌分期”提升一个等级的可能性是原来的1.120倍(95%CI：1.063~1.181，P<0.001)。“低收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“高收入”水平患者的0.411倍(95%CI：0.205~0.825，P=0.012)。所建立的模型有统计学意义(χ²=35.292，P<0.001)。

五、分析小技巧

• 有序logistic回归模型分析结果除了常数项不同，各模型的自变量系数都相同。平行性检验的目的即是验证自变量不同取值对因变量的影响系数是否相同，即要满足无论因变量的分割点在什么位置，模型中各个自变量对因变量的影响不变。
• 如果不满足平行性假设，则考虑使用无序多分类logistic回归或用不同的分割点将因变量变为二分类变量，分别进行二项logistic回归。但是，当样本量过大时，平行线检验会过于敏感。即当存在平行性时，也会显示P<0.05。此时，可以尝试将因变量设置为哑变量，并拟合多个二项logistic回归模型，通过观察自变量对各哑变量的OR值是否近似来判断。