在前面文章中介绍了条件logistic回归分析(Conditional Logistic Regression Analysis)的假设检验理论,本篇文章将实例演示在SPSS软件中实现条件logistic回归分析的操作步骤。
关键词:SPSS; 条件logistic回归; 配对logistic回归; 条件逻辑回归; 配对逻辑回归
一、案例介绍
某肾内科医师拟探究急性肾损伤的危险因素,回顾性收集了109例在院内发生急性肾损伤患者的性别、年龄、体质指数(BMI)、血肌酐(Cr)和血清乳酸(Serum Lactate),并根据性别和年龄进行1:1配对,收集了109例未发生肾损伤的患者的相关信息,进行配对病例对照研究。“sAKI”为二分类变量,代表急性肾损伤发生情况(“发生”为“1”,“未发生”为“0”);“BMI”为有序多分类变量,代表体质指数(“偏瘦”为“1”,“正常”为“2”,“超重”为“3”);“Cr”和“Lactate” 都为连续变量,分别表示血肌酐和血清乳酸含量;“subclass”为多分类变量,表示对子数。部分数据见图1。本文案例可从“附件下载”处下载。
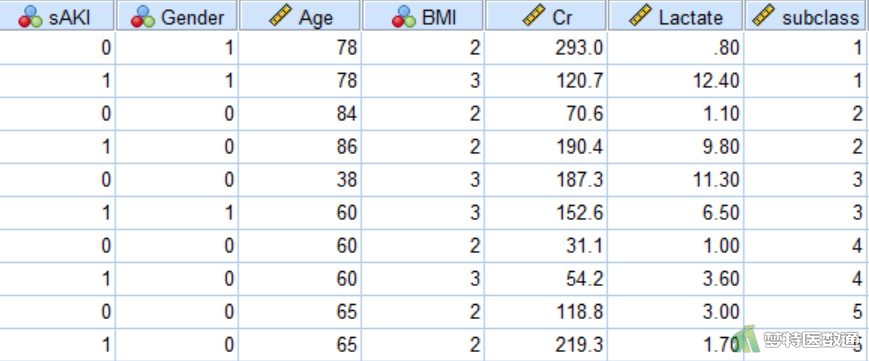
二、问题分析
本案例的分析目的是探讨某肾内科医师拟探究急性肾损伤的危险因素,采用配对设计,研究多个因素对二分类因变量的影响,可以采用条件logistic回归分析。但需要满足7个条件:
条件1:因变量为二分类变量。本研究中因变量为是否发生急性肾损伤“是”和“否”,为二分类变量,该条件满足。
条件2:至少有1个自变量。自变量可以是分类变量也可以是连续变量。本研究中有多个自变量,类型各异,该条件满足。
条件3:观察变量为配对设计。本研究中,两组患者是根据性别和年龄进行1:1配对,该条件满足。
条件4:因变量对子数为自变量个数的10~15倍(EPV原则),最好>30对,自变量的参照水平组不应少于30或50例。该条件需要通过软件分析后判断。
条件5:自变量之间无多重共线性。该条件需要通过软件分析后判断。
条件6:自变量不存在显著的异常值。该条件需要通过软件分析后判断。
条件7:数据未出现完全分离或拟完全分离现象。该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 适用条件判断1
1. 条件4判断(因变量样本例数)
首先计算因变量中例数较少类的样本例数。
(1) 软件操作
① 选择“分析”—“描述统计”—“频率”(图2)。
② 在“频率”对话框中将变量“sAKI”选入右侧“变量”框中,点击“确定”(图3)。
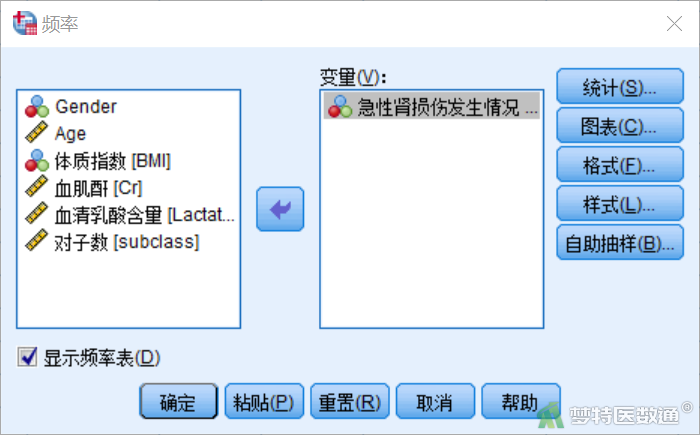
(2) 结果解读
由图4可见,“1”代表“发生急性肾损伤”,“0”代表“未发生急性肾损伤”,两组均为109例,即109对。根据“因变量对子数为自变量个数的10~15倍(EPV原则)”,本案例可纳入7~11个自变量进行多因素条件logistic回归分析。
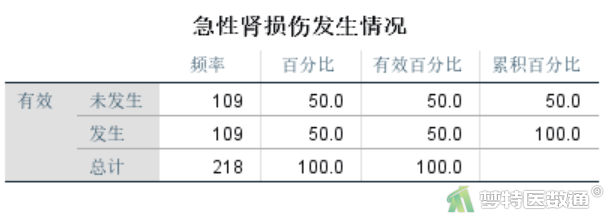
2. 条件4判断(自变量样本例数)
(1) 软件操作
(1) 软件操作
① 选择“分析”—“描述统计”—“交叉表”(图5)。
② 在“交叉表”对话框中将变量“sAKI”选入“行”,将分类变量“BMI”选入“列”(图6),然后点击“确定”。
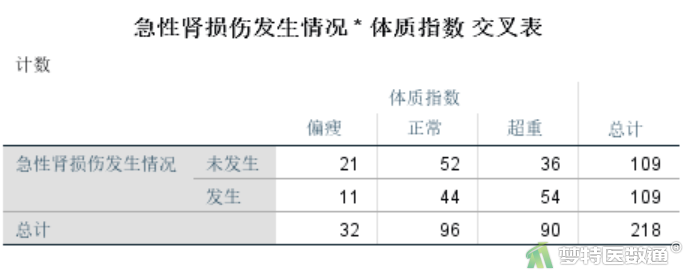
(2) 结果解读
由图7“交叉表”可知,“BMI”水平为“1”偏瘦时,因变量的例数<30,如果该变量在多因素分析过程中进入模型,应注意避免例数较少的水平被选为参照。
3. 设置哑变量
容忍度(Tolerance)或方差膨胀因子(VIF)可以用来诊断自变量之间的多重共线性。SPSS的广义线性模型不能提供这两个指标,可以通过线性回归来获得。进行线性回归的共线性诊断前需要对多分类变量设置哑变量,以下将对多分类变量“BMI”进行哑变量设置。
(1) 软件操作
① 点击“转换”—“创建虚变量”(图8)。
② 在“创建虚变量”对话框中将变量“BMI”选入右侧“针对下列变量创建虚变量”框中,然后在“创建主效应虚变量”下的“根名称-每个选定变量各一个”中输入虚拟变量的名称“BMI”。点击“确定”,完成虚拟变量设置(图9)。
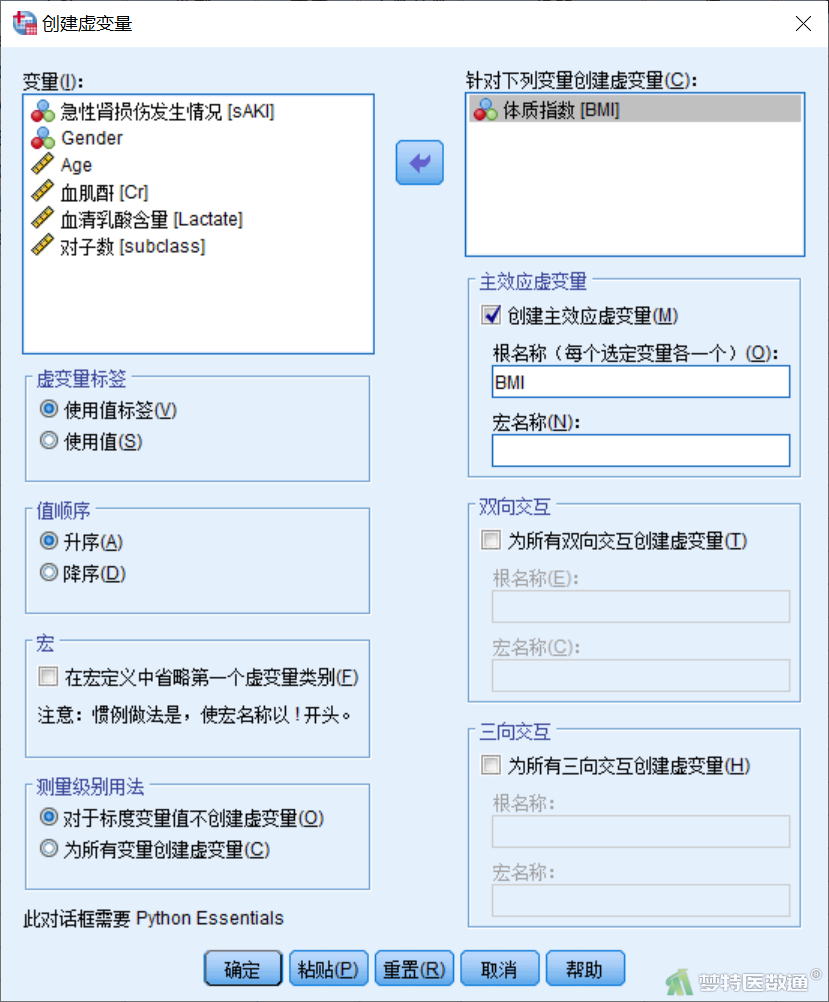
(2) 结果解读
上述步骤运行结束后可以在数据编辑页面看到新生成的3个哑变量(图10),随后就可以进行多重共线性诊断。
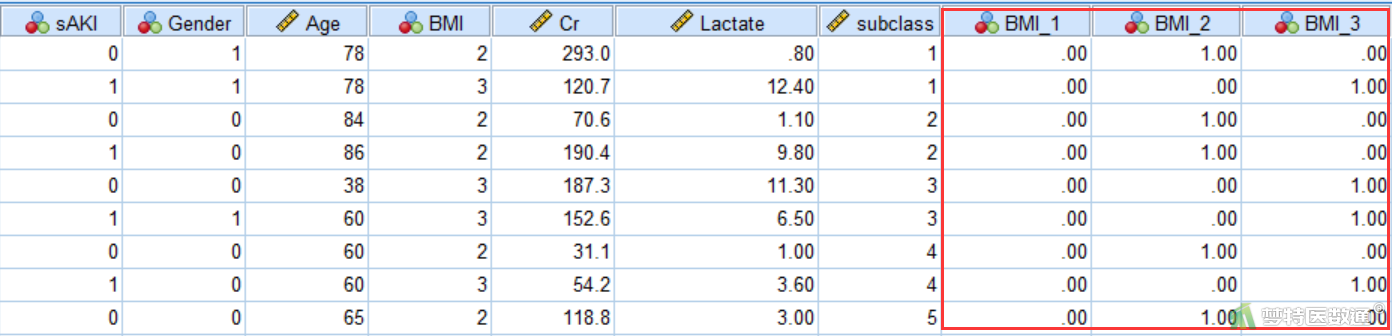
4. 条件5判断(多重共线性诊断)
(1) 软件操作
① 点击“分析”→“回归”→“线性”(图11)。

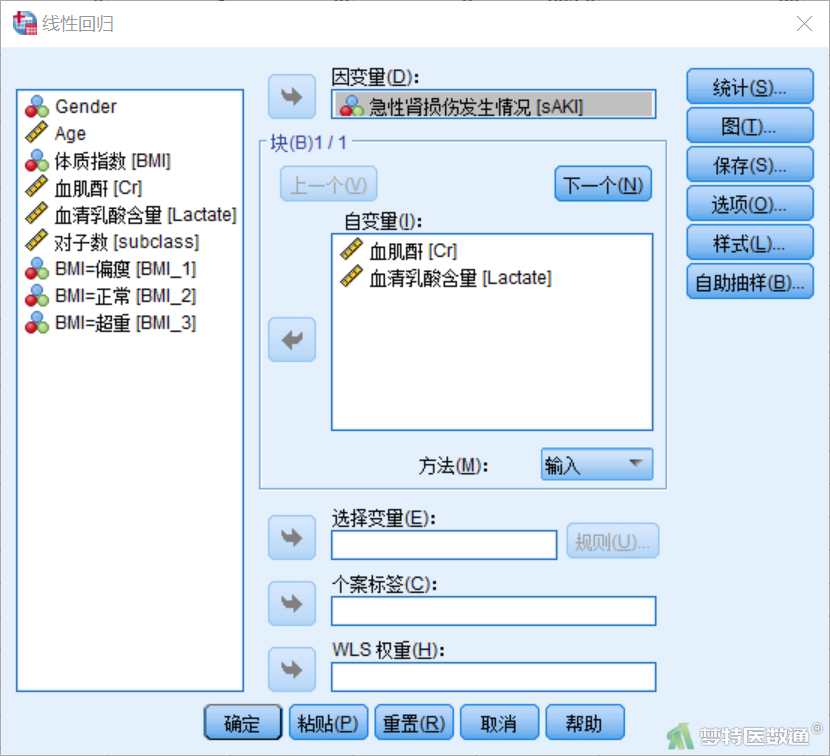
② 将变量“sAKI”选入“因变量”,变量“Cr”和“Lactate”选入“自变量”(图12)。然后点击“下一个”,在图13中将“BMI_1”和“BMI_2”2个虚拟变量同时选入右侧“自变量”,此时表示以“BMI_3”为参照水平;“方法”选择“输入”,即哑变量设置的同进同出原则。
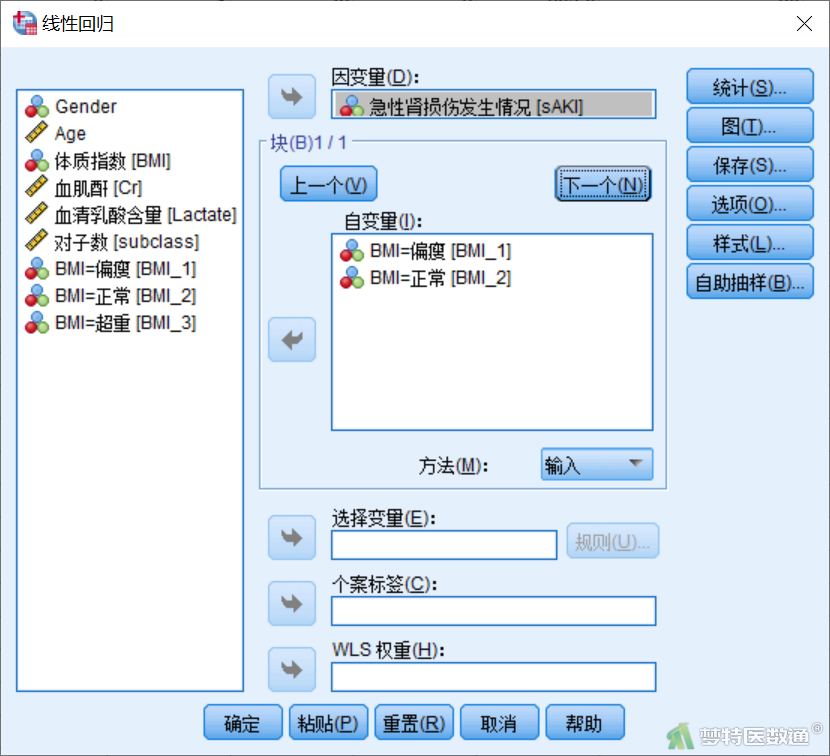
③ 点击“统计”,在“统计”子对话框中勾选“共线性诊断”(图14),点击“继续”后回到主对话框,点击“确定”。
(2) 结果解读
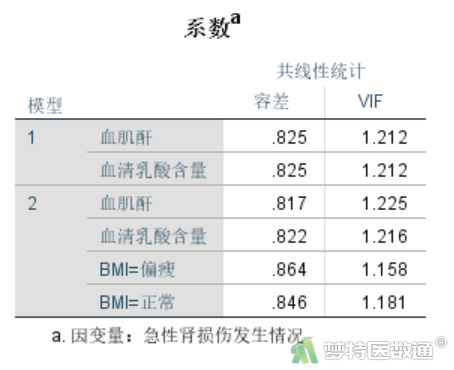
如果“容差”小于0.1或“VIF(方差膨胀因子)”大于10,则提示有严重共线性存在。本例中(图15),各变量的容忍度均远大于0.1,方差膨胀因子均远小于10,提示自变量之间不存在严重多重共线性。如果数据存在严重多重共线性,需用复杂的方法进行处理,其中最简单的是剔除引起共线性的因素之一,剔除哪一个因素可以基于理论依据。满足条件5。
5. 条件6判断(异常值检测)
(1) 软件操作
① 点击“分析”→“回归”→“二元Logistic回归”(图16)。
② 在“Logistic回归”对话框中将变量“sAKI”选入“因变量”,所有自变量“BMI”、“Cr”和“Lactate”选入“协变量”。其他保持默认不变,如图17所示。
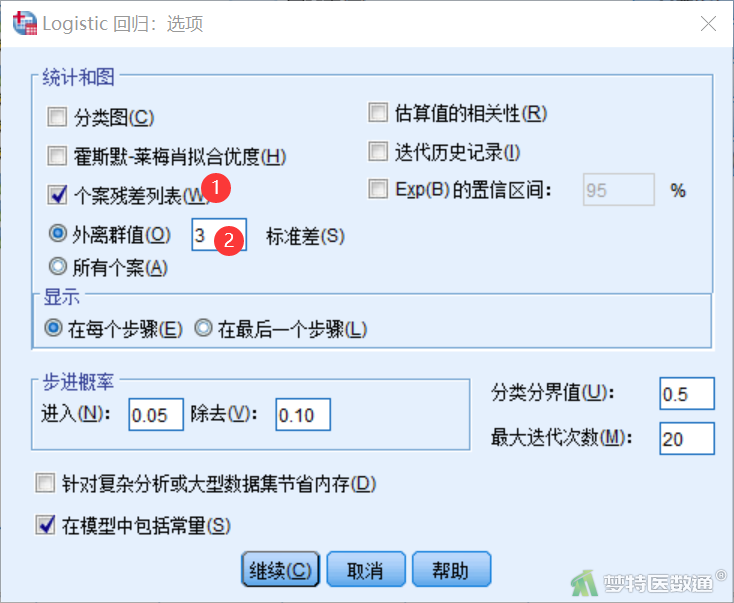
③ 点击“选项”,在“选项”子对话框中,选中“个案残差列表”。下方的“外离群值”在本案例中定义为超出3个标准差,其他设置如图18所示。点击“继续”回到主对话框后点击“确定”。
(2) 结果解读
图19显示了学生化残差大于三个标准差的观测值,显示第149条记录中有离群值,需要研究者进一步观察决定该数据是否是需要处理的异常值,此处暂以不剔除为例继续进行分析。

6. 条件7判断(完全分离检测)
完全分离,指某一个自变量本身或者某几个自变量的线性组合,对因变量的预测结果与实际情况完全一致,常表现为OR值无穷大。通过图7可见并不存在完全分离。该条件满足。
(二) 生成虚拟时间
在SPSS中没有为条件Logistic模型提供直接拟合的方法,但通过模型原理,将数据格式进行变换后可以采用其他方法拟合,常用的有变量差值拟合和分层Cox模型拟合。前者只适用于1:1配对设计,后者应用范围更广,1:1配对、1:r配对或n:m配对时都可使用。本案例将介绍通过分层Cox模型拟合法进行条件Logistic回归。运用该方法前,需要增加一个虚拟的时间变量。
① 点击“转换”→“计算变量”(图20)。
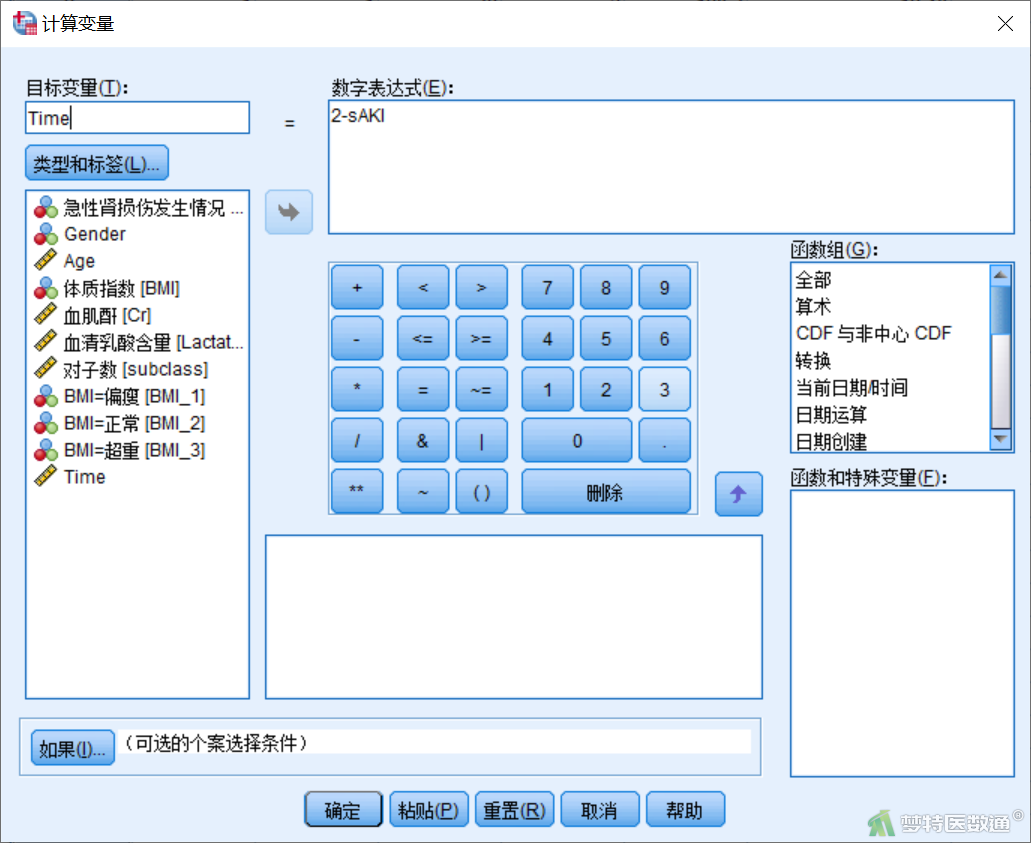
② 在“计算变量”对话框的“目标变量”处输入“Time”,“数字表达式”处输入“2-”,然后选中左侧的变量“sAKI”,点击中间的箭头,将变量输入到数字表达式中,如图21所示,(此处生成的虚拟时间要保证对照组数值大于病例组,即虚拟的生存时间对照组比病例组长,也可以选用其他数值减去sAKI)。最后点击“确定”。
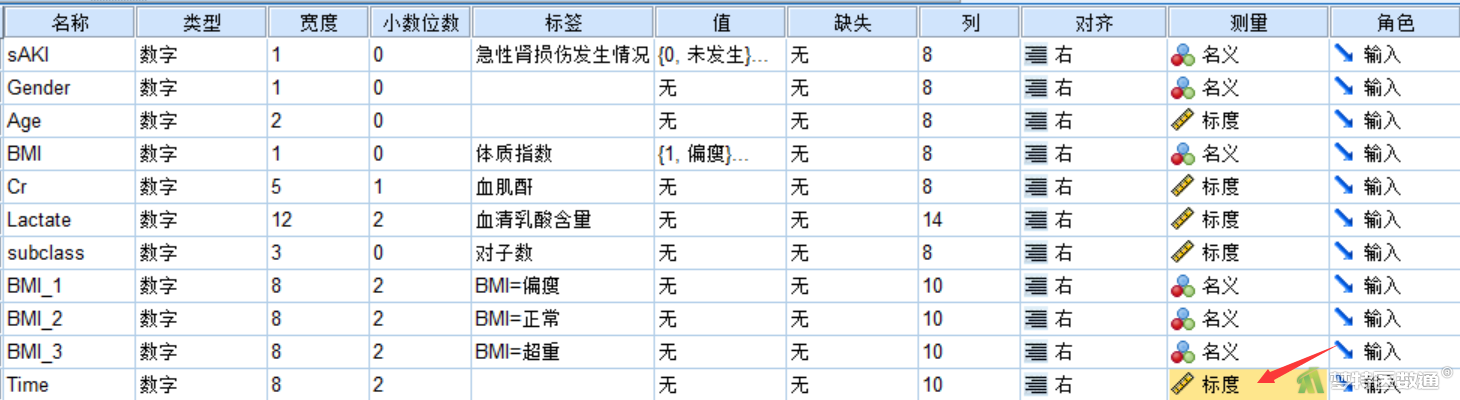
③ 完成以上步骤后即生成虚拟时间变量“Time”,在“变量视图”中将其“测量”改为“标度”(图22)。
(三) 统计描述及推断
1. 软件操作
① 点击“分析”—“生存分析”—“Cox回归”(图23)。
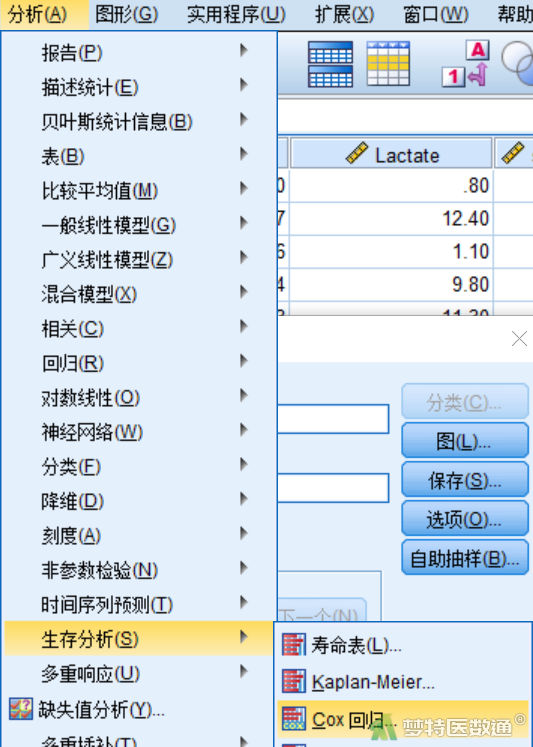
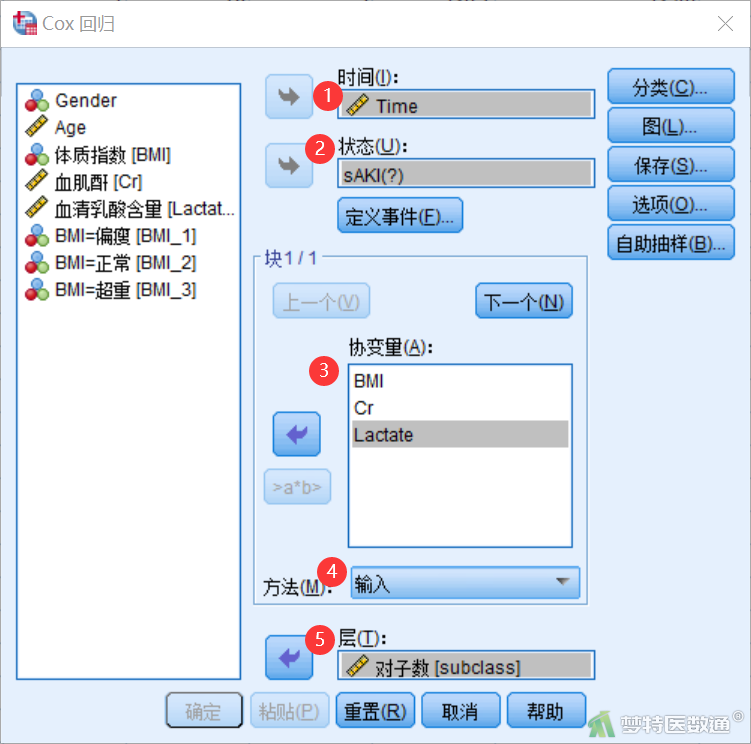
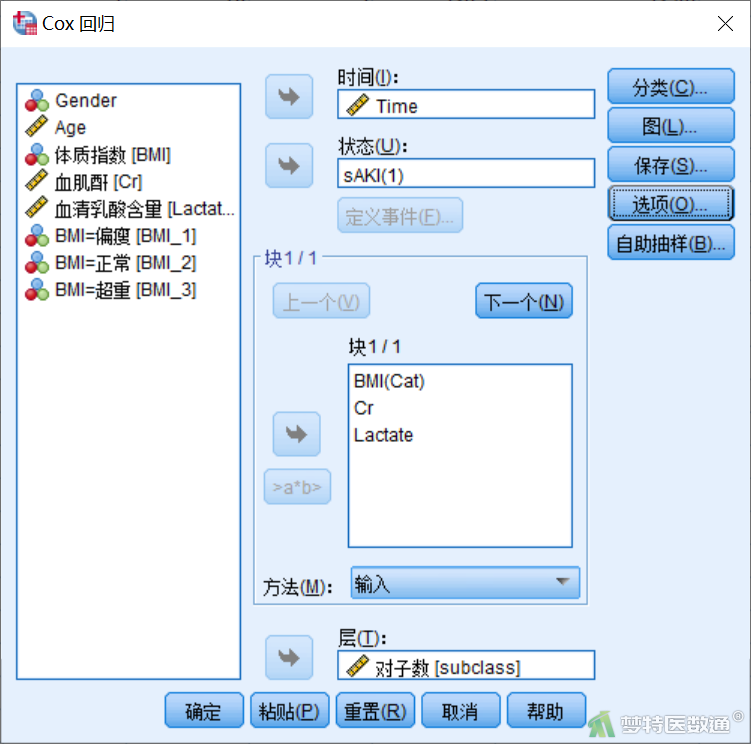
② 在“Cox回归”对话框中将变量“Time”选入“时间”下的变量框,将变量“sAKI”选入“状态”下的变量框。将变量“BMI”、“Cr”、和“Lactate”选入“协变量”中,保持默认的“输入”法,将变量“subclass”选入“层”中,如图24所示。
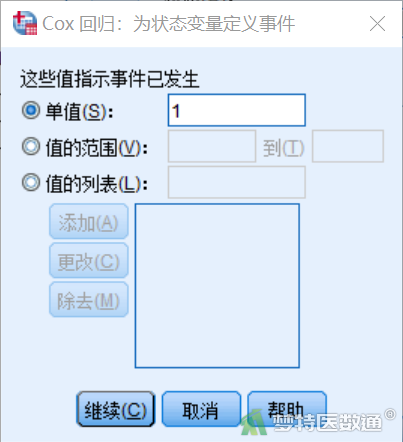
③ 点击“状态”下方的“定义事件”,在弹出框中设定代表事件发生的赋值。本案例中赋值“1”代表事件发生,故选中“单值”并在其后的录入框中录入“1”,如图25所示,点击“继续”回到主对话框。
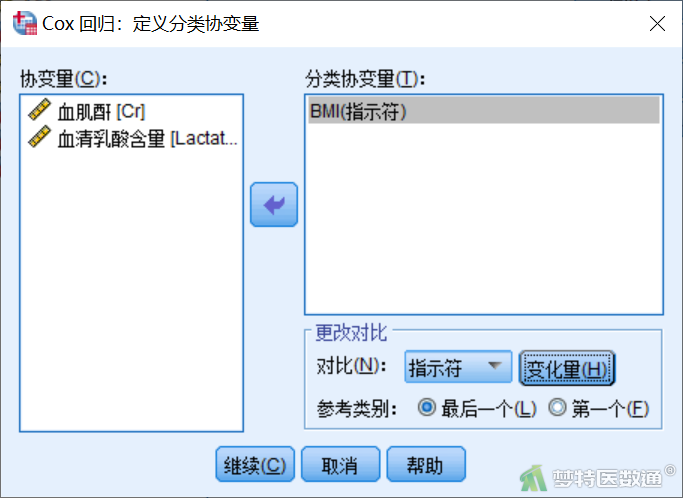
③ 点击“分类”,在子对话框中将左侧协变量框中的“BMI”选入右侧分类协变量列表框中,下方参照类别默认“最后一个”,即以BMI超重组作为参照,此处保持该选择不变,如图26所示。点击“继续”,回到主对话框中后点击“确定”。
③ 点击“选项”,在子对话框中勾选“Exp(B)的置信区间”,保持默认的“95%”。其他不变,点击“继续”,如图27所示,回到主对话框,最终完成以上步骤后主对话框如图28所示,然后点击“确定”。

2. 结果解读
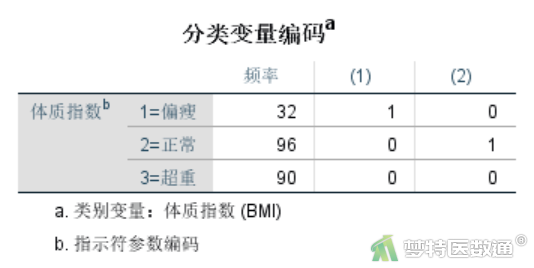
(1) 变量赋值
图29是分类自变量的描述与赋值。“频数”表示各类别个数。对于分类自变量,回归分析模型中的系数表示其他类别与参照类别的对比,所以首先要明确参照类别。此处赋值均为“0”的表示参照组,即分类变量BMI以超重组做为对照组,与上述在“分类”子对话框中选择的以BMI最后一类为参照相一致。
(2) 模型评价
图30“模型系数的Omnibus检验”是对模型的综合检验,检验是否至少有一个自变量有意义。此处χ²=47.558,P<0.001,模型有统计学意义,说明模型纳入的自变量中至少有一个有统计学意义。
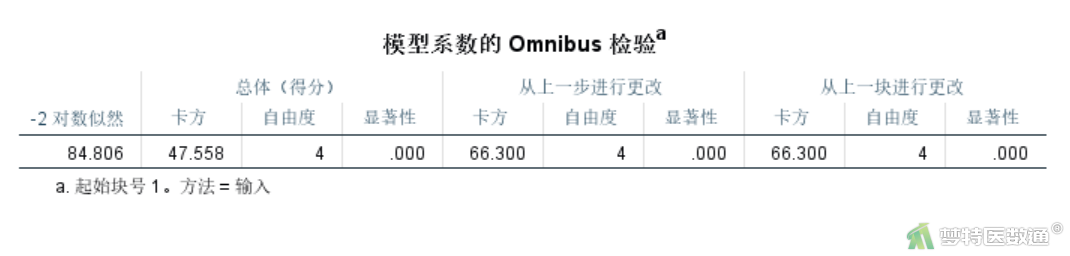
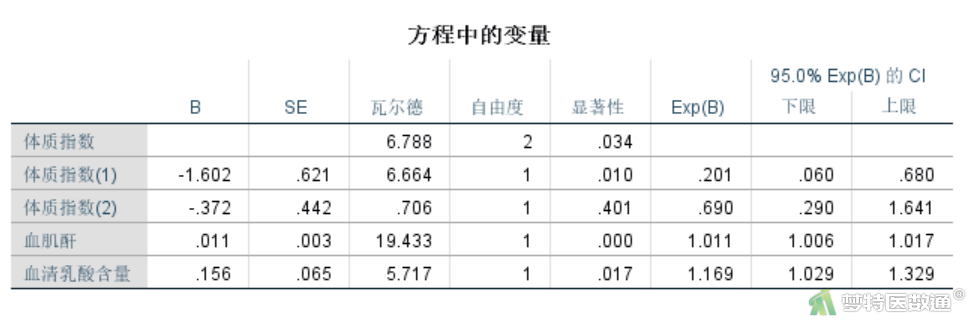
图31是对模型中每一个自变量的检验。可见三个变量的P值分别为0.034、0.000和0.017,均小于0.05,有统计学意义,表示这三个变量都与是否发生急性肾损伤有关。其中BMI(1)组的P值为0.010,系数Exp(B)为0.201(即OR值),说明BMI偏瘦和超重相比,偏瘦发生急性肾损伤的风险是超重的0.201倍 (95%CI:0.060~0.680)(将0.201取倒数,即为超重组发生急性肾损伤的风险是偏瘦组的4.98倍),BMI(2)组的P值大于0.05,说明BMI中等和BMI超重之间的差异无统计学意义。Cr组和Lacate组的系数Exp(B)分别为1.011和1.169,均大于1,说明急性肾损伤风险随着Cr和Lacate的增高而增加,Cr每增高一个单位,发生急性肾损伤的风险增加0.011倍 (95%CI:0.006~0.017;P<0.001);Lacate每增高一个单位,发生急性肾损伤的风险增加0.169倍 (95%CI:0.029~0.329;P=0.017)。
四、结论
本研究采用条件Logistic回归探讨急性肾损伤的危险因素。因变量对子数和自变量个数满足需求,变量之间不存在严重共线性和异常值,数据不存在完全分离现象。
三个自变量经过分析后发现均有统计学意义,其中BMI偏瘦发生急性肾损伤的风险是超重的0.201倍 (95%CI:0.060~0.680;P=0.010);急性肾损伤风险随着Cr的增高而增加,Cr每增高一个单位发生风险增加0.011倍 (95%CI:0.006~0.017;P<0.001);急性肾损伤风险随着Lacate的增高而增加,Lacate每增高一个单位发生风险增加0.169倍 (95%CI:0.029~0.329;P=0.017)。所建立的模型有统计学意义(χ²=47.558,P<0.001)。