最小一乘法(Least Absolute Deviation)——SPSS软件实现

关键词：SPSS; 一般线性模型; 最小一乘法; 最小二乘法

一、案例介绍

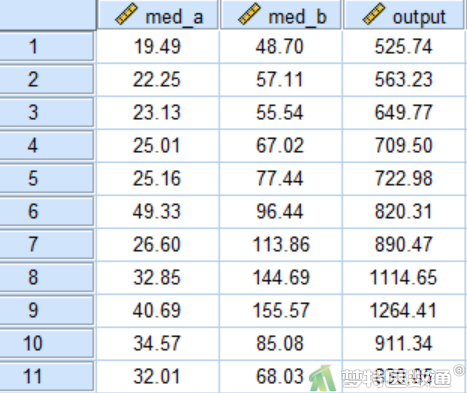
某公司新研发出一种抗抑郁药物，现猜测该药物的生产主要与A、B两种中药有关，欲探究该药物产量(output)是否受到两种中药(med_a、med_b)消耗量的影响。对数据的变量进行标签赋值后部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是分析某种抗抑郁药物产量是否受到两种中药消耗量的影响。针对这种情况，可以使用最小二乘法或最小一乘法拟合回归模型。其中最小二乘法要求残差平方和最小，对异常值的耐受能力较差；而最小一乘法要求残差的绝对值之和最小，稳健性更好。后者需要满足3个条件：

条件1：自变量与因变量均为连续变量。本研究中，为连续变量，该条件满足。

条件2：自变量与因变量之间存在线性关系，可通过绘制散点图予以考察。

条件3：线性回归过程中存在强离群点(异常值)，且强离群点不适合直接剔除有实际意义。本研究可通过绘制散点图予以考察。

三、适用条件判断

条件2-3均可以通过绘制散点图进行判断。

(一) 软件操作

①选择“图形”—“图标构建器”(图2)。

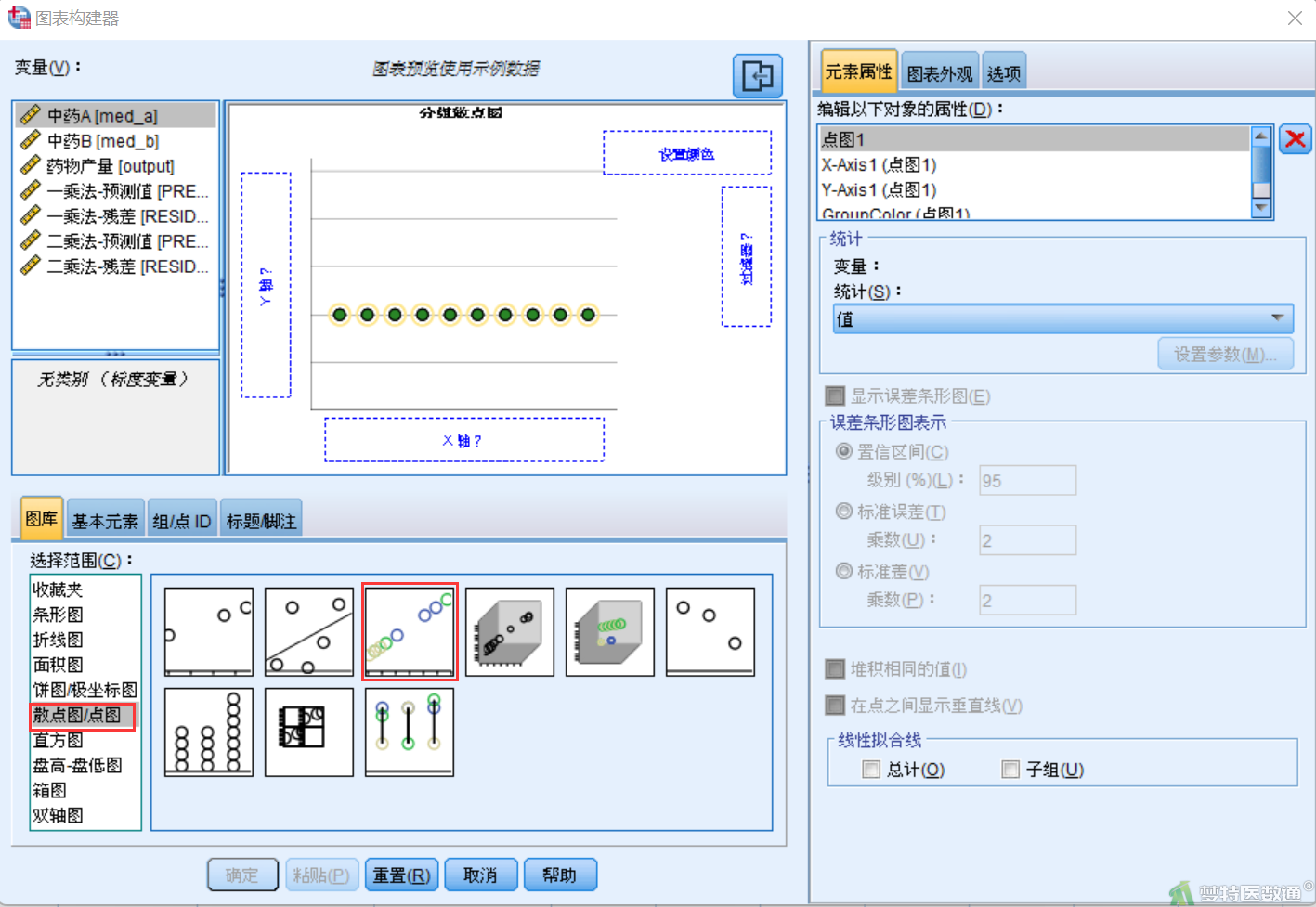
②在“图表构建器”对话框的“图库”中，选择“散点图/点图”，双击选择“包括拟合线的简单散点图” (图3)。

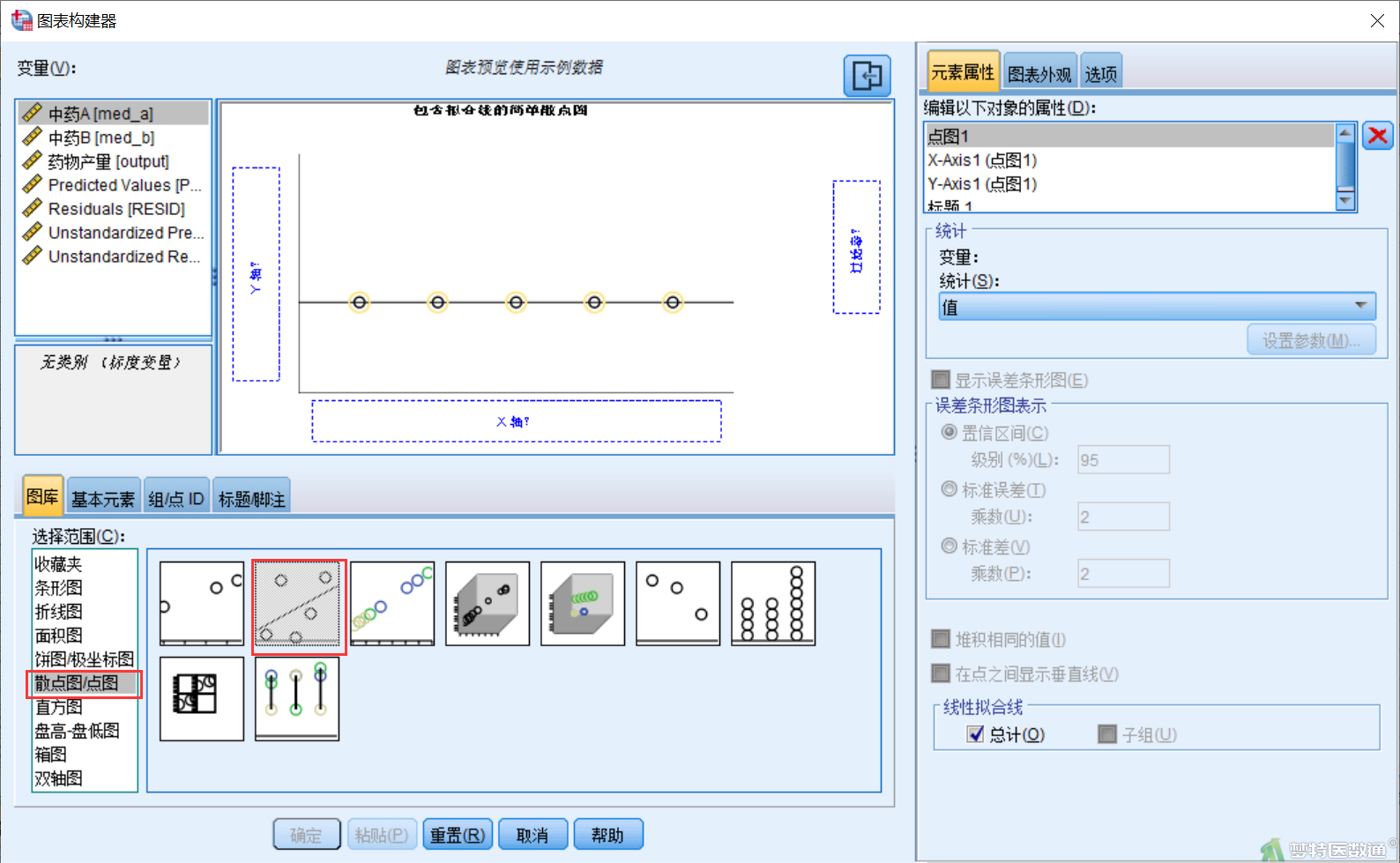
③将自变量“med_a”和因变量“output”分别拖拽到“X轴”、“Y轴”(图4)，点击“确定”，即可得散点图。自变量“med_b”和因变量“output”的散点图操作相同。

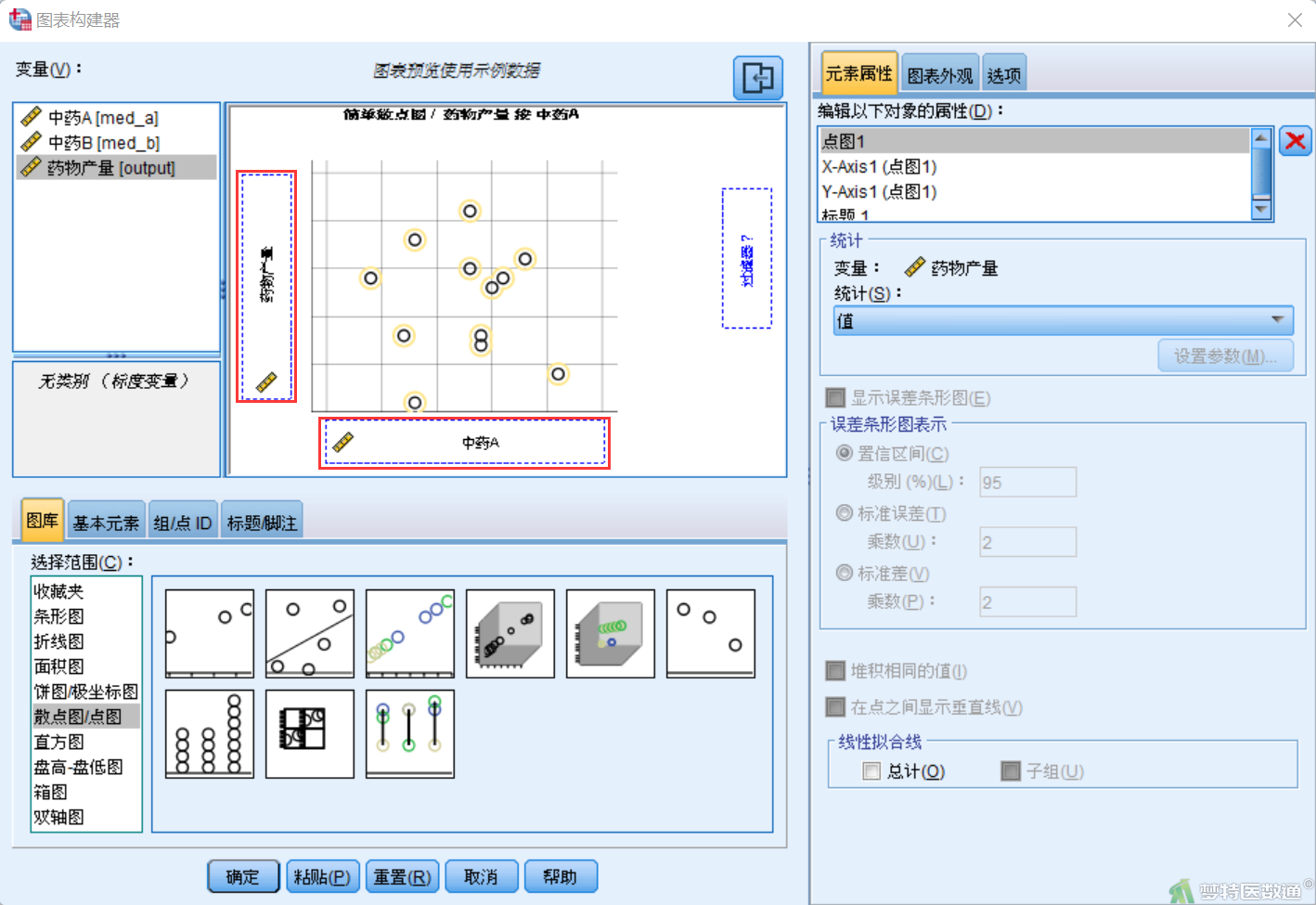
(二) 结果解读

1. 线性关系判断

图5和图6分别是A、B两个自变量和因变量分布的散点图，从图中可以看出，自变量“med_a”和自变量“med_b”均与因变量“output”存在线性关系，满足条件2。

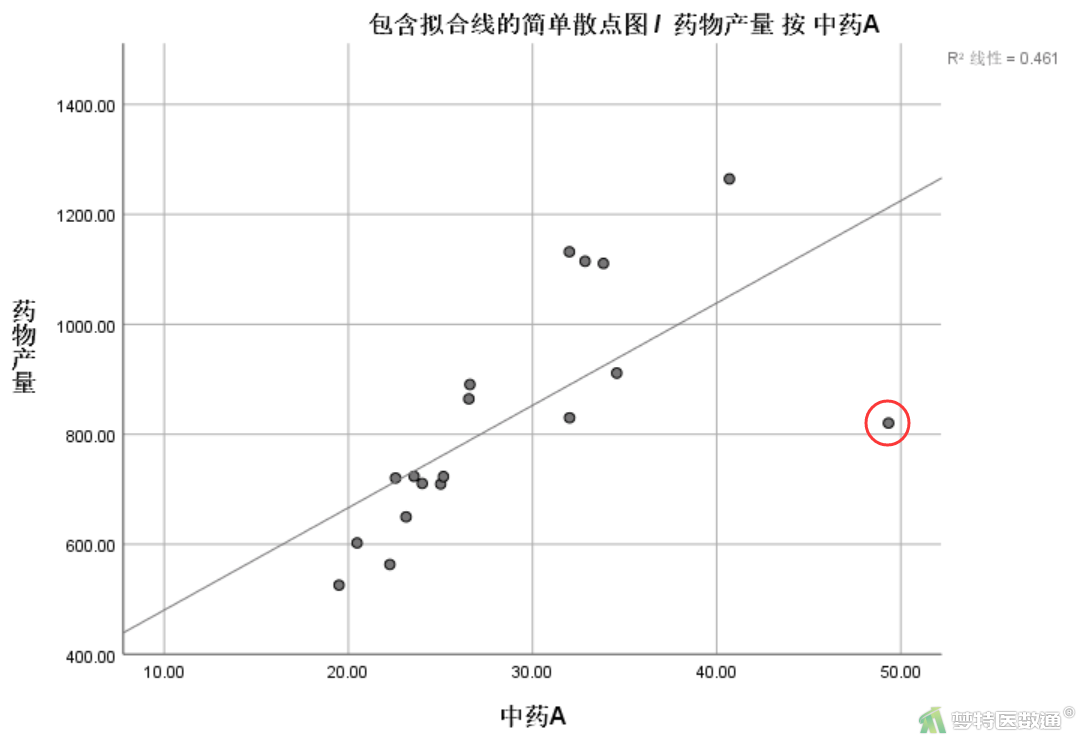
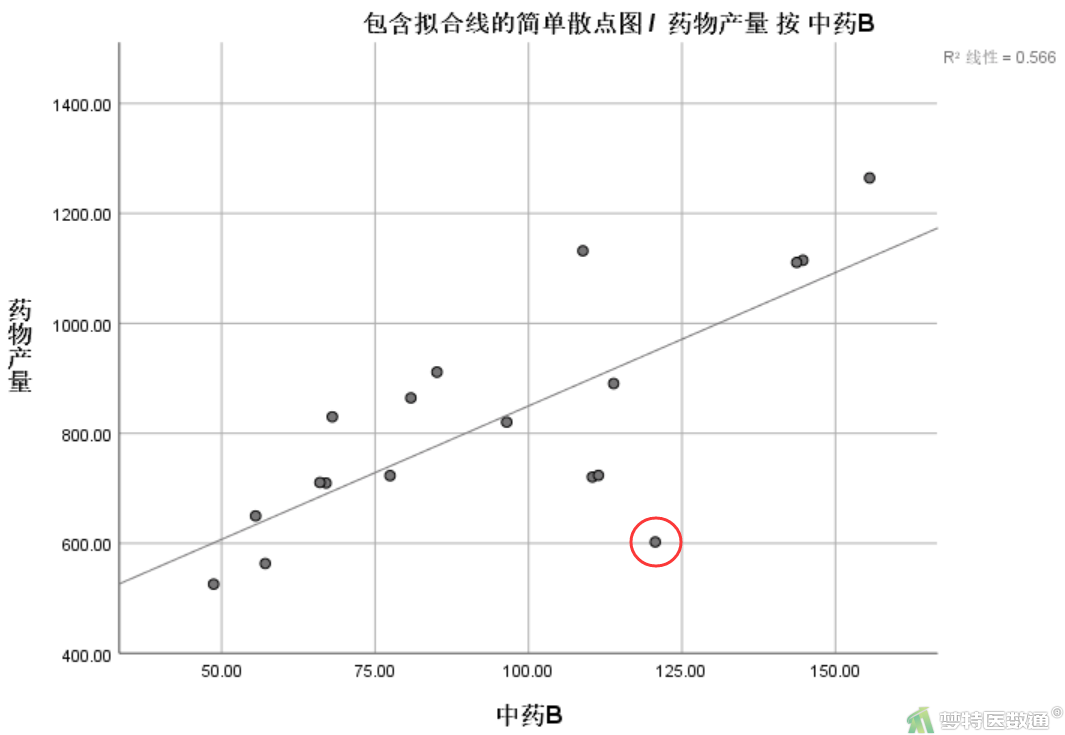
2. 异常值判断

图5和图6可以看出，各有一个散点偏离主要趋势较远，在统计模型中表现为强影响点，条件3满足。

因此，该案例选择最小一乘法进行非线性回归模型的拟合。

四、最小一乘法

(一) 软件操作

①选择“分析”—“回归”—“非线性回归”(图7)

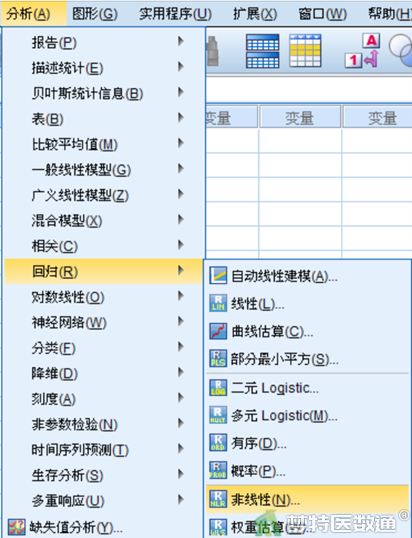
②在“非线性回归”对话框中将变量“output”选入右侧“因变量”框，在“模型表达式”框中输入“a+b1*med_a+b2*med_b” (图8)。

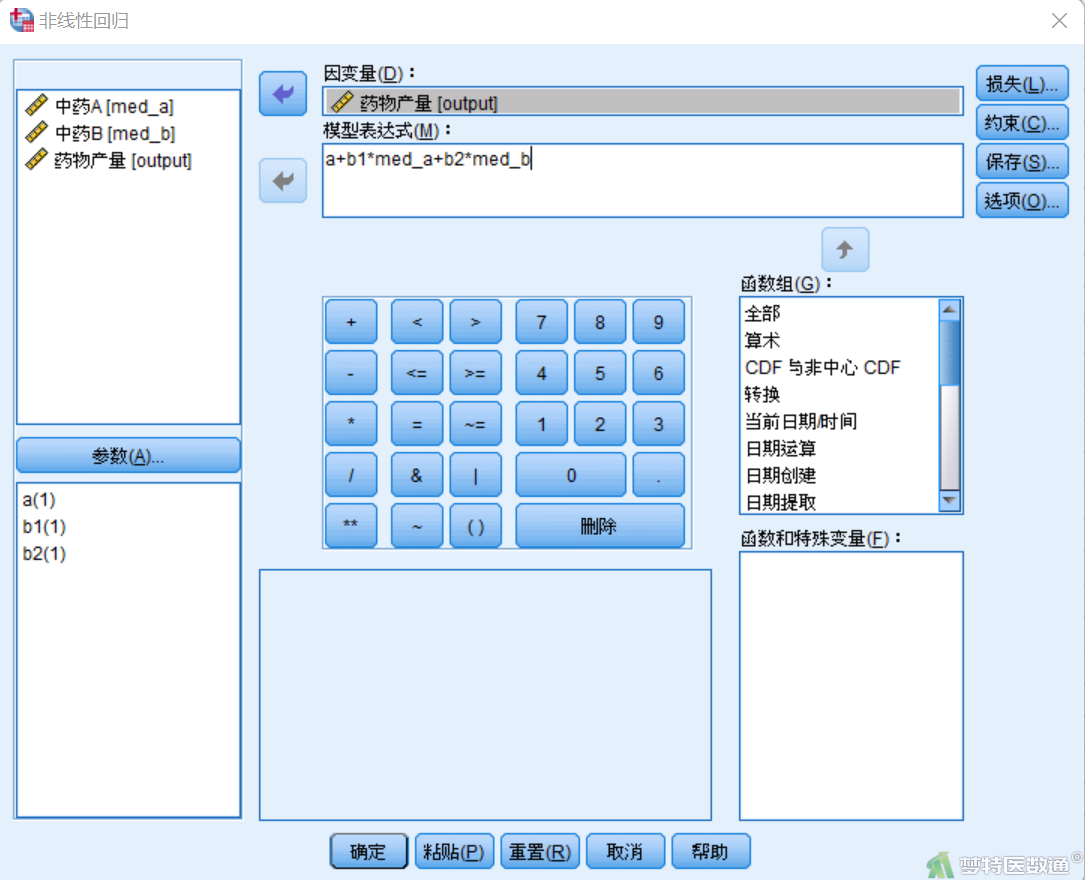
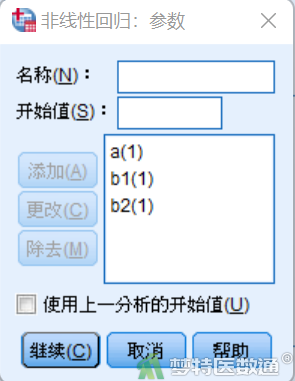
③点击“参数”按钮，将a、b1、b2的初始值均设定为“1” (图9)

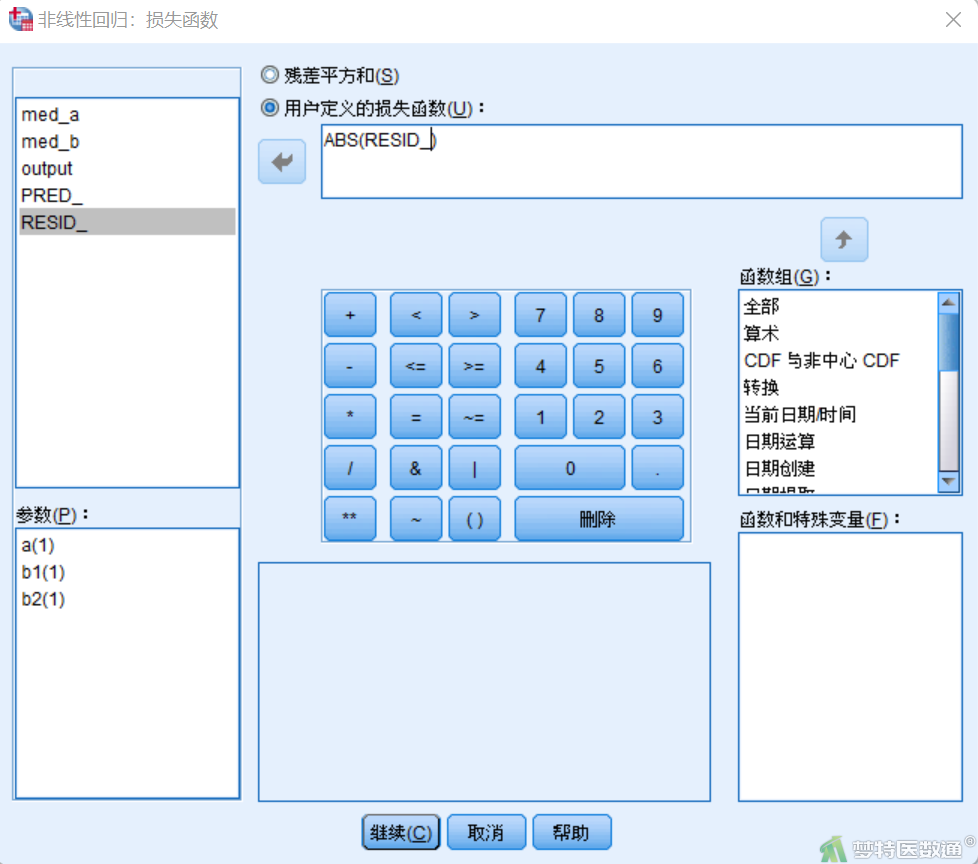
④点击“损失”按钮，在“用户定义的损失函数”框中输入“ABS(RESID_)” (图10)，其中RESID_表示变量残差，ABS()为绝对值函数。点击“继续”，将会出现图11所示提示框，继续点击“继续”即可。

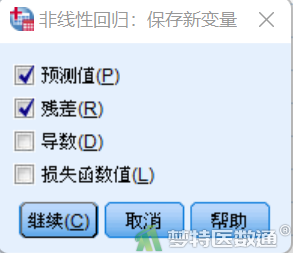
⑤点击“保存”按钮，在“保存新变量”框中勾选“预测值”和“残差” (图12)，新生成变量命名为“PRED_1”和“RESID_1”

回到主对话框后点击“确定”，则可得到统计结果。

(二) 结果解读

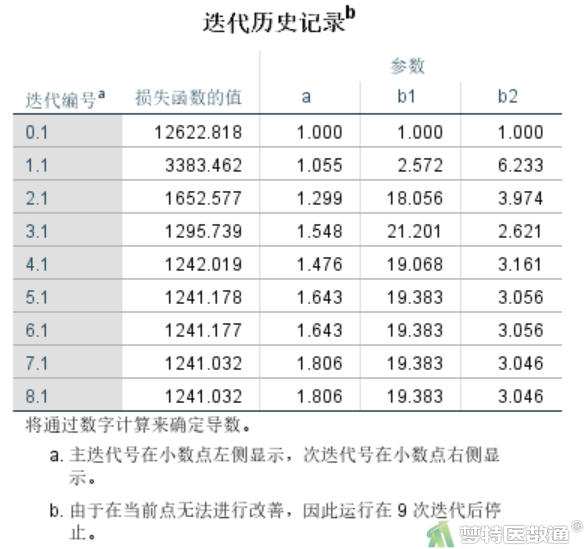
由于最小一乘法在统计理论上无法如同最小二乘法进行严密的推导，所以分析结果非常简单，仅给出了迭代计算过程，最终迭代终止时的参数值即为参数估计值。图13为结果输出的迭代计算记录，总共进行了9次迭代计算，相应的损失函数为1241.032，即残差的绝对值之和为1241.032。根据第9次的结果，可以写出经过最小一乘法拟合之后，得到的回归方程结果为：

抗抑郁药产量=1.806+19.383*中药A+3.046*中药B

根据此方程输入相关自变量数值即可对药物产量进行预测。

五、模型拟合效果验证

为了验证本案例中最小一乘法拟合非线性回归模型的效果，需要与最小二乘法进行比较。本案例如果采用最小二乘法拟合模型，结果为：

抗抑郁药产量=143.841+11.814*中药A+3.625*中药B

可见两种方法拟合的模型中，常数项和各自变量的系数均存在较大差距。但需要注意的是，常用的判断模型效果的决定系数、剩余标准差等指标都是基于最小二乘法推导而来，因此无法直接使用这些指标来判断最小一乘法结果，此时可以绘制残差分布图来直观地判断两种结果的效果。

通过上述操作，已经得到了最小一乘法的残差(RESID)和预测值(PRED)，接下来需要通过线性回归过程计算出最小二乘法的残差和预测值，接着做出两者的残差分布图，具体操作如下。

(一) 软件操作

①选择“分析”—“回归”—“线性回归”(图14)

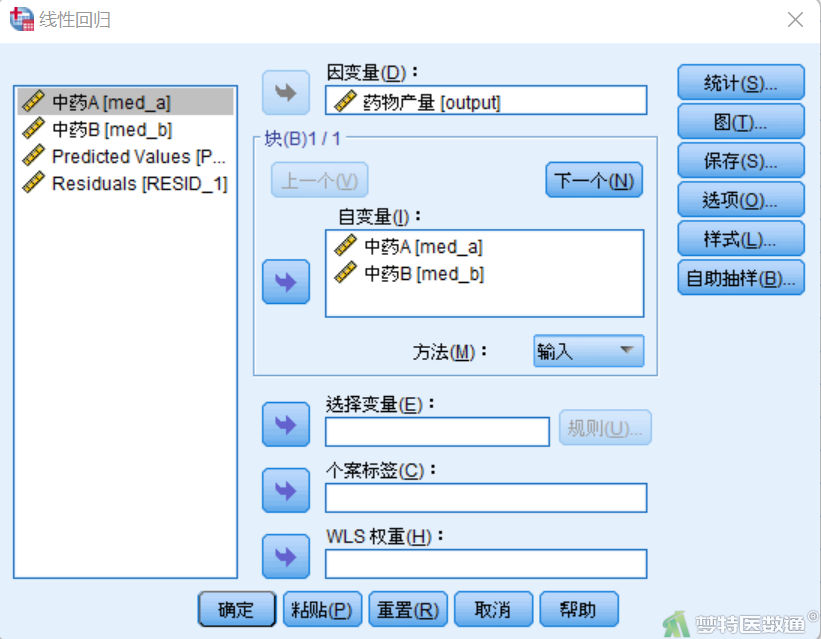
②在“线性回归”对话框中将变量“output”选入右侧“因变量”框，将变量“med_a”和“med_b”选入右侧“自变量”框 (图15)

③点击“保存”按钮，选择“预测值”中的“未标准化”选项，选择“残差”中的“未标准化”选项 (图16)，回到主对话框后点击“确定”，则可得到新生成变量并命名为“PRED_1”和“RESID_1”。

④选择“图形”—“图标构建器”，在“图表构建器”对话框的“图库”中，选择“散点图/点图”，双击选择“分组散点图”(图17)

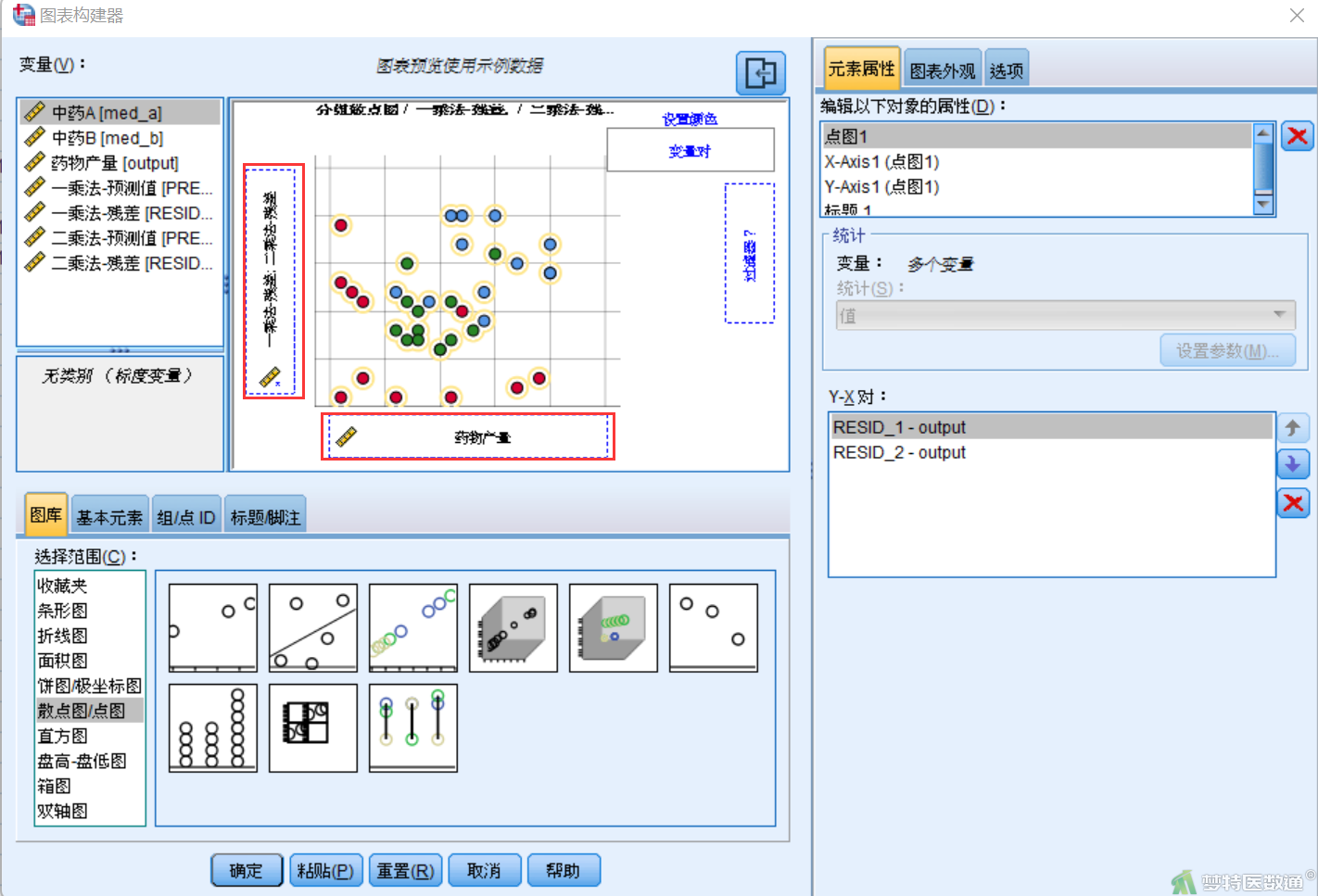
⑤将实测值作为自变量“output”拖拽到“X轴”，再将因变量“RESID”和因变量“RESID_1”分别拖拽到“Y轴”(图18)，点击“确定”，即可得散点图。

(二) 结果解读

图19展示了生成的最小一乘法和最小二乘法的残差和预测值

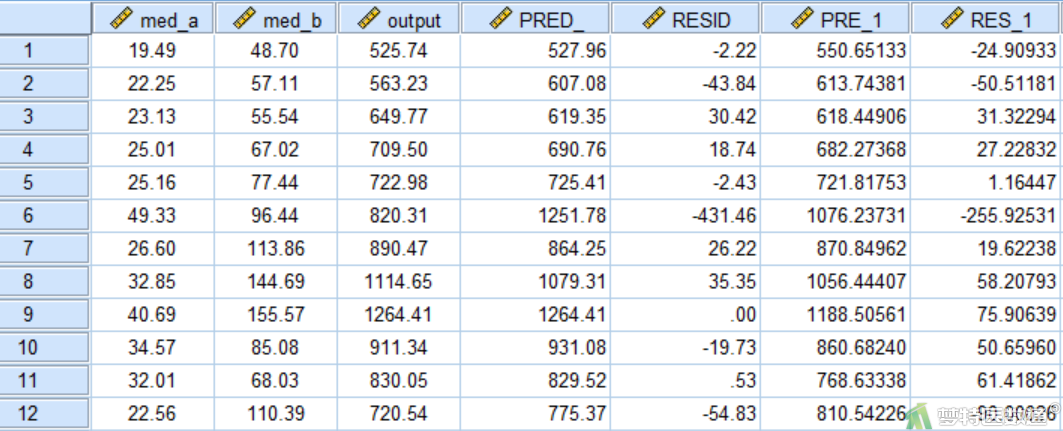
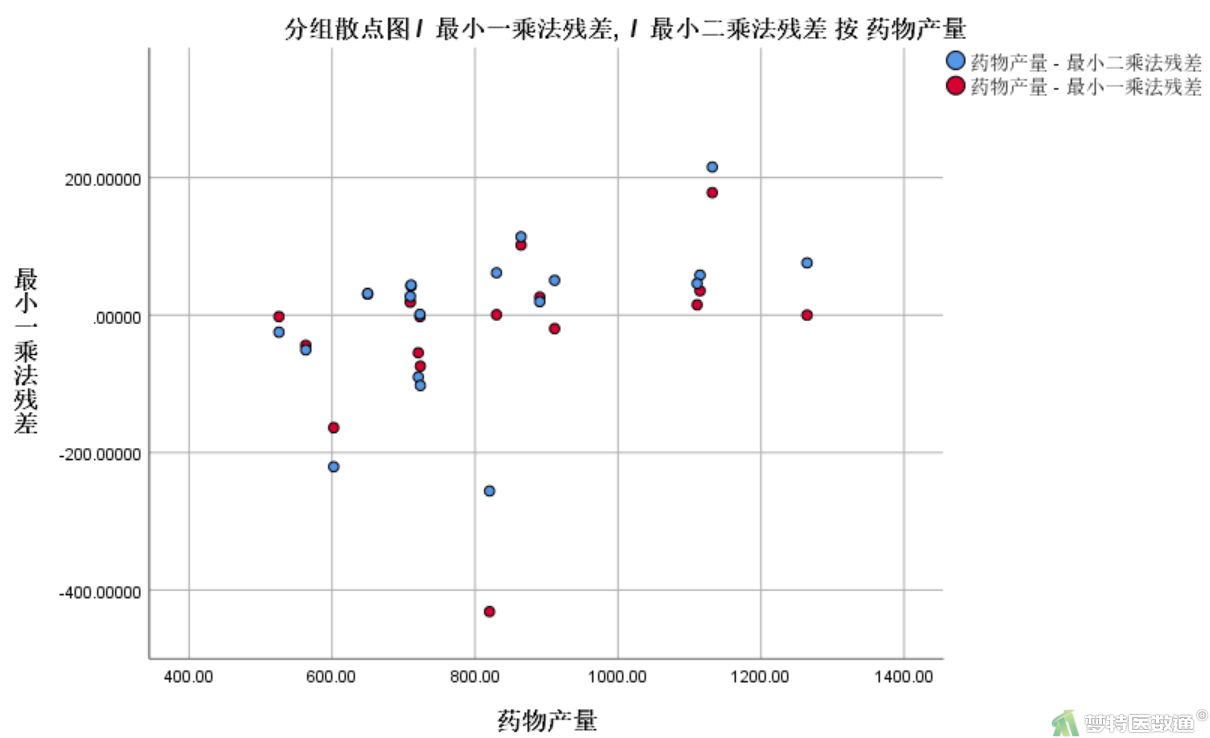
图20为将实测值作为横轴，最小一乘法和二乘法的残差作为纵轴所做的散点图，可知对于大部分记录，最小一乘法的预测残差都要小于最小二乘法残差，这说明一乘法模型对大部分散点的拟合效果是比二乘法好的。但对于红框中的两个数据点，最小一乘法的残差明显大于最小二乘法，这说明最小一乘法对于强影响点(异常值)更有耐受力。因此，最小一乘法对大多数散点的拟合效果比最小二乘法好，但对于个别强影响点的拟合效果是更差的。

六、结论

本研究采用最小一乘法分析某种抗抑郁药物产量是否受到两种中药消耗量的影响。通过绘制散点图，提示两个自变量与因变量均存在线性关系，且数据中存在强影响点(异常值)导致主要趋势发生偏移。非线性回归分析方程为：抗抑郁药产量=9.441+19.561*中药A+3.024*中药B。

七、知识小贴士

• 当数据中存在异常值(极端值)，随机误差不服从正态分布时，最小二乘法拟合效能较低，可选择一些替代方法：如最小一乘法、加权最小二乘法、自回归模型等。
• 参数初始值的设定：如果可变为线性，可以先拟合线性方程，将此结果作为初始值；如果方程可解，则代入若干样本值，解出近似取值作为初值；先拟合较简单的雏形，将结果作为初始值。
• 损失函数(loss function)或代价函数(cost function)：是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数。最小一乘法中自定义损失函数为残差绝对值。
• 最小一乘法结果仅展示参数估计值，无检验和标准误差的估计结果。