二分类Logistic回归分析(Binomial Logistic Regression Analysis)——Python软件实现

关键词：Python; 二分类logistic回归; 二项logistic回归; 二元logistic回归; 逻辑回归; EPV原则

一、案例介绍

探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素，纳入146例治疗效果“不佳”(记录为1)的患者，278例治疗效果“良好”(记录为0)的患者，并收集其余变量信息。其余变量及编码为性别(gender：0=女，1=男)、年龄(age，0=60岁以下，1=60岁及以上)、手术时间(time, min)、突出部位(part, 1=单侧，2=中央，3=极外侧)、突出分类(class, 1=膨出型，2=突出型，3=脱垂型)、Modic改变(modic, 1=I级，2=II级，3=III级)、是否钙化(cal, 0=未钙化，1=钙化)、矢状径(d, cm)、退变级别(level, 1=I-III级，2=IV级，3=V级)。部分数据见图1。本案例数可从“附件下载”处下载。

二、问题分析

本案例的分析目的是探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素，由于因变量是二分类变量，因此可以使用二分类logistic回归分析。但需要满足7个条件：

条件1：因变量为二分类变量。本研究中因变量是治疗效果“不佳”和“良好”，为二分类变量，该条件满足。

条件2：至少有1个自变量。自变量可以是分类变量也可以是连续变量。本研究中有多个自变量，类型各异，该条件满足。

条件3：各观测行间相互独立。对研究设计和数据收集的过程进行分析，可判断本案例中观测值之间不存在互相影响的情况。

条件4：例数较少类的因变量例数为自变量个数的10~15倍(EPV原则)，且经验上两组的人数最好＞30例，参照水平组不应少于30或50例。该条件需要通过软件分析后判断。

条件5：自变量之间无多重共线性。该条件需要通过软件分析后判断。

条件6：自变量不存在显著的异常值。该条件需要通过软件分析后判断。

条件7：数据未出现完全分离或拟完全分离现象。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

import pandas as pd
df = pd.read_csv(r'二分类Logistic回归.csv')  #导入CSV数据
pd.set_option('display.max_rows', 10)
df  #查看数据

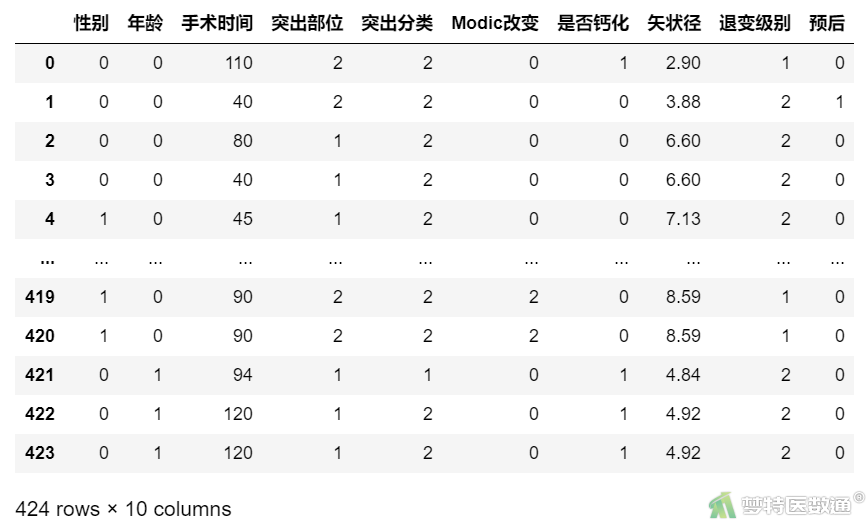
图1

在数据栏目(图1)中可以查看全部数据情况，数据集中共有10个变量和424个观察数据，10个变量分别为性别、年龄、手术时间、突出部位、突出分类、Modic改变、是否钙化、矢状径、退变级别及预后。

(二) 适用条件判断

1. 条件4判断(自变量样本例数)

为了增加结果的可读性，给部分分类变量增加标签，之后再逐一计算分类变量各类别的因变量例数，即生成R*C列联表。

(1) 软件操作

##给变量添加标签label ##

df2 = df.copy()
df2.loc[df2['性别']== 1 ,'性别']='男'
df2.loc[df2['性别']== 0 ,'性别']='女'
df2.loc[df2['年龄']== 1 ,'年龄']='60岁及以上'
df2.loc[df2['年龄']== 0 ,'年龄']='60岁以下'
df2.loc[df2['突出部位']== 1 ,'突出部位']='单侧'
df2.loc[df2['突出部位']== 2 ,'突出部位']='中央'
df2.loc[df2['突出部位']== 3 ,'突出部位']='极外侧'
df2.loc[df2['突出分类']== 1 ,'突出分类']='膨出型'
df2.loc[df2['突出分类']== 2 ,'突出分类']='突出型'
df2.loc[df2['突出分类']== 3 ,'突出分类']='脱垂型'
df2.loc[df2['Modic改变']== 0 ,'Modic改变']='I级'
df2.loc[df2['Modic改变']== 1 ,'Modic改变']='II级'
df2.loc[df2['Modic改变']== 2 ,'Modic改变']='III级'
df2.loc[df2['是否钙化']== 0 ,'是否钙化']='未钙化'
df2.loc[df2['是否钙化']== 1 ,'是否钙化']='钙化'
df2.loc[df2['退变级别']== 1 ,'退变级别']='I-III级'
df2.loc[df2['退变级别']== 2 ,'退变级别']='IV级'
df2.loc[df2['退变级别']== 3 ,'退变级别']='V级'
df2.loc[df2['预后']== 0 ,'预后']='良好'
df2.loc[df2['预后']== 1 ,'预后']='不佳'
df2

图2

#性别与预后的R*C列联表#

pd.crosstab(df2['性别'], df2['预后'])

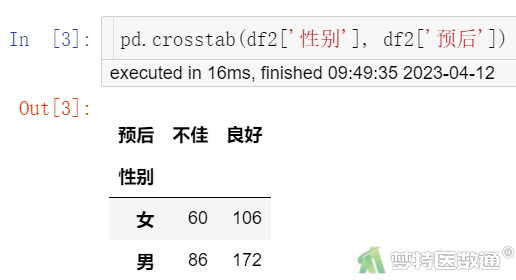
图3-1

#年龄与预后的R*C列联表#

pd.crosstab(df2['年龄'], df2['预后'])

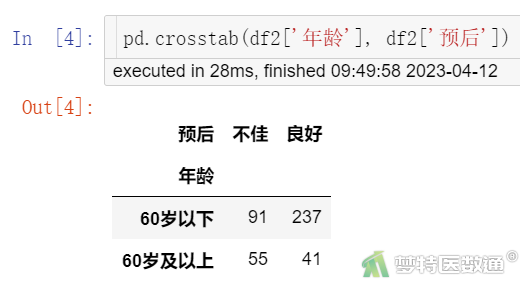
图3-2

#突出部位与预后的R*C列联表#

pd.crosstab(df2['突出部位'], df2['预后'])

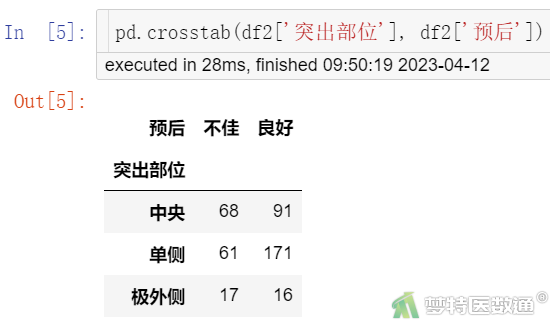
图3-3

#突出分类与预后的R*C列联表#

pd.crosstab(df2['突出分类'], df2['预后'])

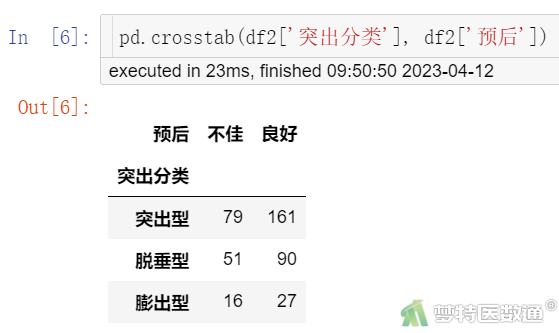
图3-4

#Modic改变与预后的R*C列联表#

pd.crosstab(df2['Modic改变'], df2['预后'])

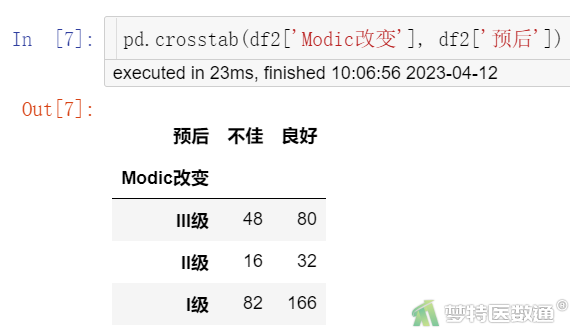
图3-5

#是否钙化与预后的R*C列联表#

pd.crosstab(df2['是否钙化'], df2['预后'])

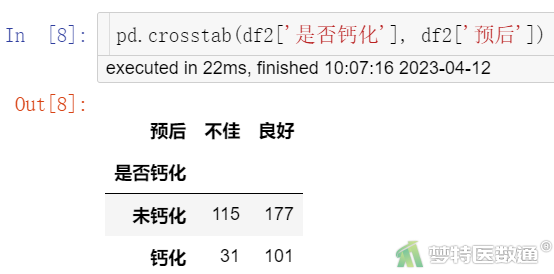
图3-6

#退变级别与预后的R*C列联表#

pd.crosstab(df2['退变级别'], df2['预后'])

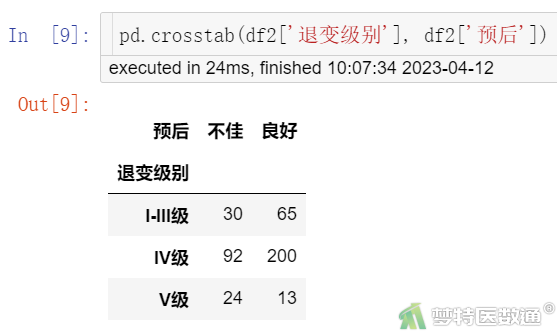
图3-7

(2) 结果解读

R*C列联表(图3-3、图3-4和图3-7)显示，突出部位水平为“极外侧”时、突出分类水平为“膨出型”时、退变级别水平为“V级”时，因变量的例数<30，如果这些变量在多因素分析过程中进入模型，应注意避免例数较少的水平被选为参照。

2. 条件4判断(因变量样本例数)

计算因变量中例数较少类的样本例数。

(1) 软件操作

##预后变量计数##

group = df2.groupby(['预后']).describe()
group

图4

(2) 结果解读

预后变量计数(图4)显示，预后不佳为146例，预后良好为278例。根据“例数较少类的因变量例数为自变量个数的10~15倍(EPV原则)”，本案例可纳入10~15个自变量进行多因素二分类logistic回归分析。

3. 条件5判断(多重共线性诊断)

详见本章后文。

4. 条件6判断(异常值检测)

详见本章后文。

5. 条件7判断(完全分离检测)

完全分离，指某一个自变量本身或者某几个自变量的线性组合，对因变量的预测结果与实际情况完全一致，常表现为OR值无穷大。通过各R*C列联表(图3-1至图3-7)可见并不存在这种情况。该条件满足。

(三) 变量筛选

1. 软件操作

因为分类变量无法直接放入模型，这里需要对其进行转换，而回归模型中对分类变量最常用的处理方法之一便是将其转化成虚拟变量(设置哑变量)。在Python中可通过删除参照水平设置哑变量。

##设置哑变量##

df3 = pd.get_dummies(df,columns=['突出部位','突出分类','Modic改变','退变级别'])
df3.drop(columns = ['突出部位_1','突出分类_3','Modic改变_0','退变级别_3'],inplace=True) #通过删除相应水平，将其设置为参考变量
df3

图5

##单因素logistic回归##

#lmreg1_性别#

import statsmodels.api as sm
x = sm.add_constant(df3.iloc[:,[0]]) #生成自变量
y = df['预后'] #生成因变量
model = sm.GLM(y, x.astype(float),family=sm.families.Binomial()) #生成模型
lmreg1 = model.fit() #模型拟合
lmreg1.summary() #模型描述

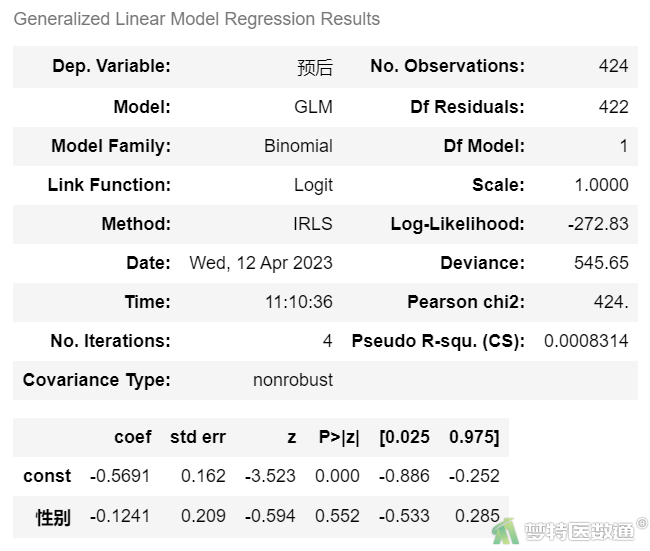
图6-1

#lmreg2_年龄#

x = sm.add_constant(df3.iloc[:,[1]]) #生成自变量
y = df['预后'] #生成因变量
model = sm.GLM(y, x.astype(float),family=sm.families.Binomial()) #生成模型
lmreg2 = model.fit() #模型拟合
lmreg2.summary() #模型描述

图6-2

#lmreg3_手术时间#

x = sm.add_constant(df3.iloc[:,[2]]) #生成自变量
y = df['预后'] #生成因变量
model = sm.GLM(y, x.astype(float),family=sm.families.Binomial())
lmreg3 = model.fit() #模型拟合
lmreg3.summary() #模型描述

图6-3

#lmreg4_是否钙化#

x = sm.add_constant(df3.iloc[:,[3]]) #生成自变量
y = df['预后'] #生成因变量
model = sm.GLM(y, x.astype(float),family=sm.families.Binomial())
lmreg4 = model.fit() #模型拟合
lmreg4.summary() #模型描述

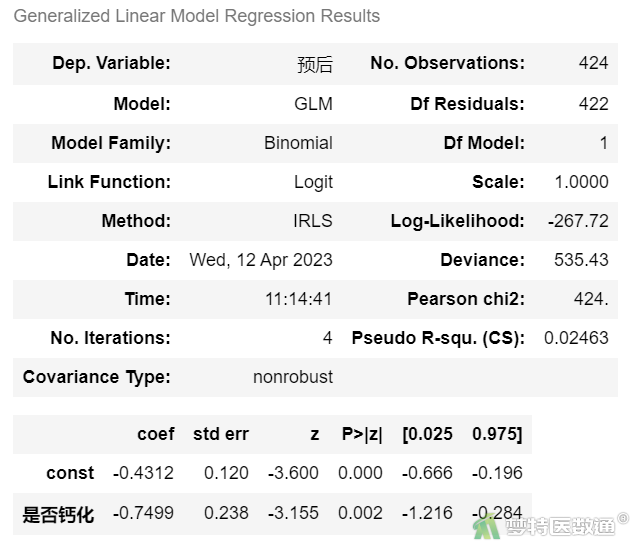
图6-4

#lmreg5_矢状径#

x = sm.add_constant(df3.iloc[:,[4]]) #生成自变量
y = df['预后'] #生成因变量
model = sm.GLM(y, x.astype(float),family=sm.families.Binomial())
lmreg5 = model.fit() #模型拟合
lmreg5.summary() #模型描述

图6-5

#lmreg6_突出部位#

x = sm.add_constant(df3.iloc[:,[6,7]]) #生成自变量
y = df['预后'] #生成因变量
model = sm.GLM(y, x.astype(float),family=sm.families.Binomial())
lmreg6 = model.fit() #模型拟合
lmreg6.summary() #模型描述

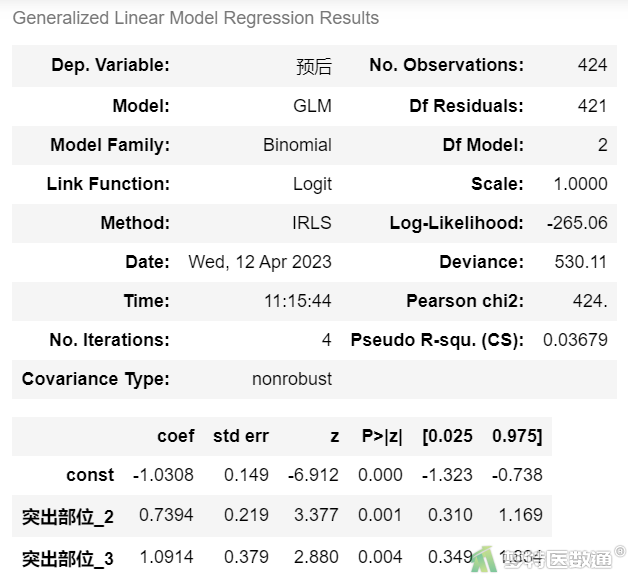
图6-6

#lmreg7_突出分类#

x = sm.add_constant(df3.iloc[:,[8,9]]) #生成自变量
y = df['预后'] #生成因变量
model = sm.GLM(y, x.astype(float),family=sm.families.Binomial())
lmreg7= model.fit() #模型拟合
lmreg7.summary() #模型描述

图6-7

#lmreg8_Modic改变#

x = sm.add_constant(df3.iloc[:,[10,11]]) #生成自变量
y = df['预后'] #生成因变量
model = sm.GLM(y, x.astype(float),family=sm.families.Binomial())
lmreg8 = model.fit() #模型拟合
lmreg8.summary() #模型描述

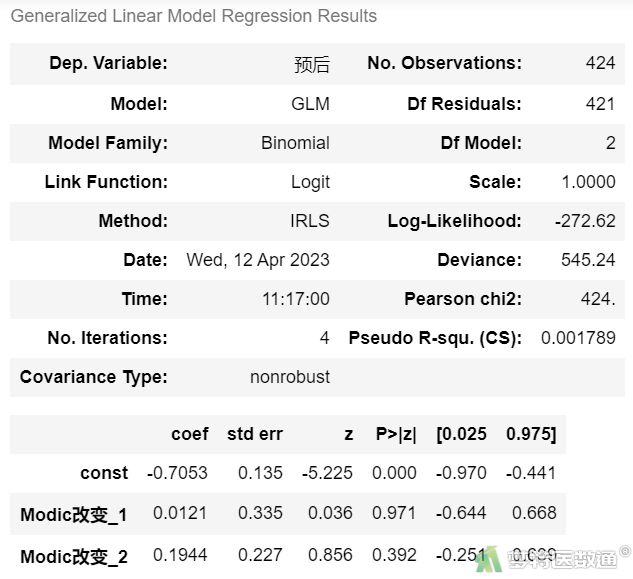
图6-8

#lmreg9_退变级别#

x = sm.add_constant(df3.iloc[:,[12,13]]) #生成自变量
y = df['预后'] #生成因变量
model = sm.GLM(y, x.astype(float),family=sm.families.Binomial())
lmreg9 = model.fit() #模型拟合
lmreg9.summary() #模型描述

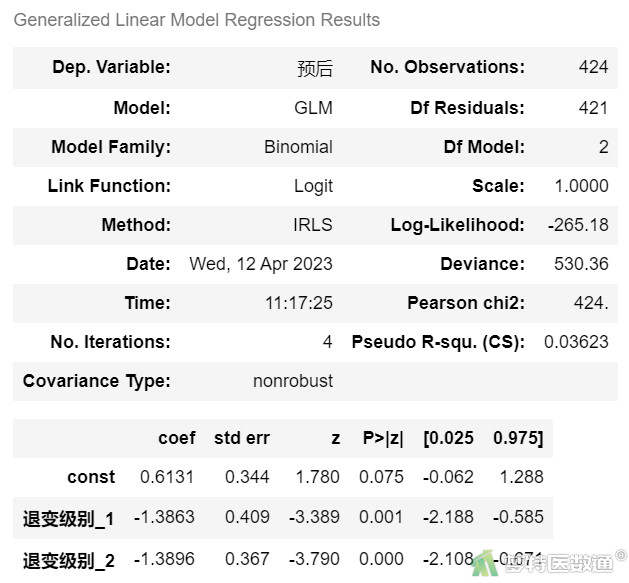
图6-9

2. 结果解读

单因素logistic回归分析结果(图6-1至6-9)显示，变量“性别”、“手术时间”、“突出分类”和“Modic改变”与因变量的关联无统计学意义，“年龄”、“突出部位”、“钙化”、“矢状经”和“退化级别”与因变量的关联有统计学意义。

(四) 适用条件判断(补充)

将“手术时间”、“性别”、“突出分类”、“Modic改变”四个无统计学意义的变量移除，建立新的回归模型后进行如下操作。

1. 条件5判断(多重共线性诊断)

(1) 软件操作

##建立新的回归模型##

#lmreg10_年龄、突出部位、钙化、矢状经、退变级别#

x = sm.add_constant(df3.iloc[:,[1,3,4,6,7,12,13]]) #生成自变量
y = df['预后'] #生成因变量
model1 = sm.GLM(y, x.astype(float),family=sm.families.Binomial())
lmreg10 = model1.fit() #模型拟合
lmreg10.summary() #模型描述

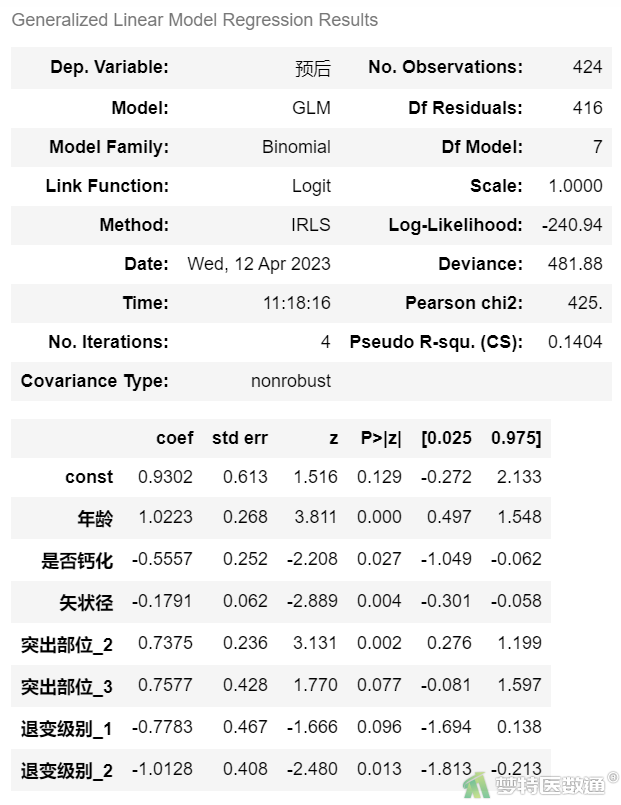
图7

##共线性诊断##

from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = [variance_inflation_factor(df3.drop(['预后','性别','手术时间','突出分类_1','突出分类_2','Modic改变_1','Modic改变_2'],axis = 1), i) for i in range(df3.drop(['预后','性别','手术时间','突出分类_1','突出分类_2','Modic改变_1','Modic改变_2'],axis = 1).shape[1])]
pd.DataFrame(data = zip(df3.drop(['预后','性别','手术时间','突出分类_1','突出分类_2','Modic改变_1','Modic改变_2'],axis = 1),vif),columns = ['变量','vif'])  #计算vif

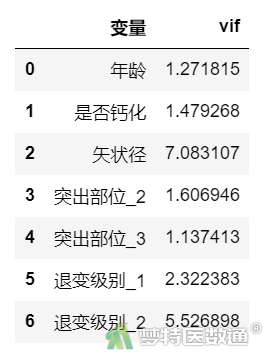
图8

(2) 结果解读

自变量的方差膨胀因子(variance inflation factor，VIF)计算结果(图8)显示，所有自变量的VIF均<10，提示自变量之间不存在严重共线性问题。

2. 条件6判断(异常值检测)

(1) 软件操作

##计算cook距离##

infl = lmreg10.get_influence()
cook_d = infl.cooks_distance[0]
print(max(cook_d))

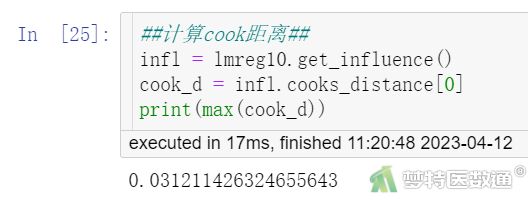
图9

(2) 结果解读

最大库克距离(cook’ distance)结果(图9)为0.031<0.5，提示不存在显著异常值，本研究数据满足条件6。

(五) 模型拟合

1. 软件操作

##计算OR ##

import numpy as np
OR = np.exp(lmreg10.params)
print(OR)

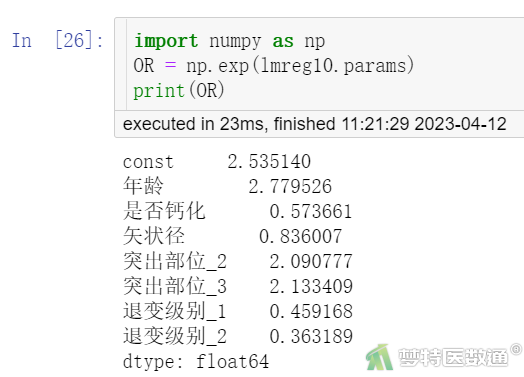
图10

2. 结果解读

模型详细参数(图7)显示了截距和自变量的“coef (非标准化系数)”、“std err(标准误)”，统计量z、P值以及模型所有变量系数的95%CI。图10计算了OR值。OR值为e^{(回归系数)}，如矢状径的OR=0.836=e^(-0.179)，表示矢状径每增加1cm，术后效果不佳的风险降低16.4% (OR=0.836，P=0.004)。

其他自变量结果的解释分别为：年龄60岁及以上的患者术后不佳的风险约为60岁以下患者的2.780倍(P<0.001)；突出部位为“中央”和“极外侧”的患者术后效果不佳的风险分别约为“单侧”患者的2.091倍(P=0.002)和2.133倍(P=0.077)；“钙化”患者术后不佳的风险约为“非钙化”患者的0.574倍(P=0.027)；退变级别为“I-III级”的患者术后效果不佳的风险与“V级”患者相比，差异无统计学意义(P=0.096)，退变级别为“IV级”的患者术后效果不佳的风险比级别为“I-III级”的患者低63.7%(OR=0.363，P=0.013)。

(六) 预测价值

1. 软件操作

##绘制ROC曲线##

import random
from matplotlib import pyplot as plt
from sklearn.metrics import roc_curve#图11
#计算模型 得预测值#
import statsmodels.formula.api as smf #加载statsmodels.formula.api库
x = df3.iloc[:,[1,3,4,6,7,12,13]]
y = df['预后']
model1 = sm.GLM(y, x.astype(float),family=sm.families.Binomial()).fit()
y_pre = model1.predict(x)  #提取预测值赋值给pre
y_true = y # 真实值
y_proba = y_pre # 预测概率
fpr,tpr,threshold = roc_curve(y_true,y_proba)
from sklearn.metrics import auc
roc_auc = auc(fpr, tpr)
plt.figure(figsize=(5, 5))
plt.plot(fpr, tpr, color='darkorange',
         lw=2, label='AUC (area = %0.3f)' % roc_auc)  ###假正率为横坐标，真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
maxindex = (tpr - fpr).tolist().index(max(tpr - fpr))  # 找到约登指数点
plt.scatter(fpr[maxindex], tpr[maxindex], c="black", s=30)  # 截断点标记
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc="lower right", fontsize=11)
plt.show()

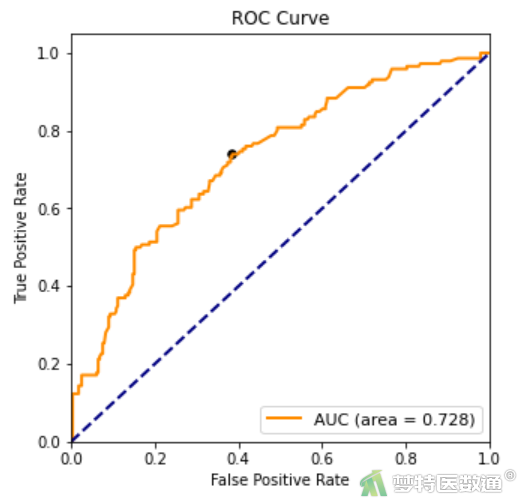
图11

2. 结果解读

ROC曲线结果(图11)显示曲线下面积为72.8%，该模型的判断效果一般。

四、结论

本研究采用二分类Logistic回归探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素。因变量例数分布满足样本量需求，变量之间不存在严重共线性和异常值，数据不存在完全分离现象。

9个自变量经过分析后，最终有5个(矢状径、年龄、突出部位、是否钙化和退变级别)进入模型。其中矢状径的OR=0.836=e^(-0.179)，表示矢状径每增加1cm，术后效果不佳的风险降低16.4% (OR=0.836，P=0.004)。年龄60岁及以上的患者术后不佳的风险约为60岁以下患者的2.780倍(P<0.001)。突出部位为“中央”和“极外侧”的患者术后效果不佳的风险分别约为“单侧”患者的2.091倍(P=0.002)和2.133倍(P=0.077)。“钙化”患者术后不佳的风险约为“非钙化”患者的0.574倍(P=0.027)。退变级别为“I-III级”的患者术后效果不佳的风险与“V级”患者相比，差异无统计学意义(P=0.096)，退变级别为“IV级”的患者术后效果不佳的风险比级别为“I-III级”的患者低63.7% (OR=0.363，P=0.013)。ROC曲线下面积为72.8%，该模型的判断效果一般。

五、多重共线性的判断及处理

• 多重共线性是指自变量间存在线性相关关系，容忍度越小、VIF越大，表明共线性越强。实际数据分析过程中，若容忍度<0.2或VIF＞5则表明存在较强共线性，若容忍度<0.1或VIF＞10则表明存在严重共线性问题。
• 在实际数据分析过程中，若存在以下情况，则暗示模型可能存在共线性问题：①整个模型的检验结果为P值≤检验水准α，但各自变量的偏回归系数检验结果却为P值＞检验水准α。②专业上认为应该有统计学意义的自变量，检验结果确无统计学意义。③自变量的偏回归系数的取值大小甚至符号明显与实际情况相违背，难以解释。④增加或删除一个自变量或一个案例，自变量偏回归系数发生较大变化。
• 自变量若存在严重多重共线性，可采取以下措施进行处理：①基于专业知识直接确认优先选择哪些变量进入模型，而将相对次要的共线性变量从模型中剔除。②逐步回归，但是当共线性比较严重时，变量自动筛选的方法并不能完全解决问题。③岭回归/lasso回归，为有偏估计，但能有效地解决共线性问题。④主成分回归法，这种方法的代价是在提取主成分时会丢失一部分信息，收益则是大大降低了共线性对参数估计值的扭曲，而且自变量间的多重共线性越强，提取主成分时丢失的信息就越少。
• 需要注意的是，多重共线性的存在不一定必然影响模型的使用价值，其理论上共线性不应当降低模型的预测效果，其影响主要是使模型的偏回归系数发生改变，从而无法得到专业上合理的解释。

六、自变量进入模型的形式

• 无序多分类自变量需要以哑变量形式进入模型，在SPSS中通过选择参照水平实现哑变量的设置，但需要注意以下事项：①参照水平要具有实际意义，否则会失去比较的目标，如“其他”一般不适宜做参照水平。②参照水平应有一定的例数(不低于30或50例)，否则将导致与其比较的其他组的置信区间较大。③哑变量整体分析无统计学意义时，所有哑变量都不用再纳入模型；整体分析有统计学意义时，尽管有些哑变量无统计学意义，但仍需要纳入模型，即“同进同出”原则。
• 有序多分类自变量进入模型有多种方式备选，但应选择最具合理性的方式：①直接以计量资料形式带入模型：此时得到的模型较为简洁，也容易解释。但应用的前提是自变量的每个水平对因变量的影响作用基本一致，可通过观察哑变量各水平的回归系数值是否存在等级变化关系进行判定。建议先将有序多分类资料分别以哑变量和连续变量的形式引入模型，观察每个哑变量的回归系数间是否存在等级关系，并对两个模型进行似然比检验，如果似然比检验无统计学意义，且每个哑变量的回归系数间存在等级关系，则可以将该自变量以连续变量形式引入模型，否则还是采用哑变量的方式引入模型。②设置哑变量：参照无序多分类资料。③当有序多分类变量的等级水平与因变量结局不成线性关系时，应采用最优尺度回归探讨效应拐点。
• 定量资料进入模型有多种方式备选，但也应选择最具合理性的方式：如果某计量资料能以计量形式进入模型(有统计学意义)，那么转化后应当同样能进入模型，且OR值会显著增加。①直接带入模型，尽管此种方法较为简单，但仍不做首选推荐。因为此时得出的OR值一般较小，即自变量变化一个单位对结局风险的影响其实是有限的，不能贴近专业解释。 如果资料分布严重失衡时(非均匀分布)尤其不能直接带入模型。但以计量资料形式直接进入模型往往模型的拟合效果较好。②根据专业意义降维后(如根据BMI指数分级标准降维为有序多分类资料)，参照有序多分类资料或者二分类资料处理方式。③如果没有专业划分标准，可以资料分布形式根据四分位数间距或等分法降维或者标准化后按Per 1 sd (每一个标准差)降维。④建立自变量和因变量之间的ROC曲线，根据约登指数进行二分类降维。⑤中位数(非正态分布)或者均数(近似正态或正态分布)降维。⑥当自变量的单位不合适导致因变量的风险改变很小时，可对自变量采取缩小(如除以100)或扩大(如乘以10)相应倍数的方式。

七、自变量的选择策略

关于自变量是否纳入多因素分析模型除了根据本章节介绍的判定方法以外，还可采取以下策略：

• 专业原则：首先需要考虑的就是专业原则，这一点最为重要。如果目前专业知识有证据表明该变量与结局发生有关，那么不论该变量单因素分析结果是否有统计学意义，都应纳入多因素分析模型。
• 以单因素分析为基础：当分析的变量较多时，可先采取单因素分析方法，对有统计学意义的变量再纳入多因素分析。此时单因素分析检验水准可设置为0.1-0.2，如果样本量较大，可将检验水准设置为较为严格；如果样本量较小可将检验水准设置较为宽松。
• 比较原则：可以尝试多种方法对该变量进行分析，如采用多种自变量进入方法分析，或将计量资料降维后再分析，如果变量在多种进入方法和不同变量类型时，均能在多因素分析模型中有统计学意义，则表明该变量的确是因变量的真正影响因素。