单因素重复测量方差分析(One-Way Repeated Measures ANOVA)——Python软件实现

关键词：Python软件; 重复测量; 重复测量资料; 重复测量方差分析; 单因素重复测量方差分析; 球形检验; 交互作用; 主效应; 单独效应

一、案例介绍

检验科研究血样放置时间对某生化指标浓度检测的影响，采集了10份人血标本，分别在放置0分钟(T0)、30分钟(T30)、60分钟(T60)和90分钟(T90)时对该指标的浓度(mmol/L)进行检测，分析放置时间是否对该生化指标检测结果有影响？数据见图1。本案例数据可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较4个时间点的生化指标浓度是否有差异。由于4个时间点的数据属于重复测量数据，可以使用单因素重复测量方差分析(One-Way Repeated Measures ANOVA)。但需要满足4个条件：

条件1：观察变量唯一，且为连续变量。本研究中观察变量为生化指标浓度，且为连续变量，该条件满足。

条件2：观察变量为重复测量数据，即不满足独立性。本研究中4个时间点测量的生化指标浓度均是针对同一批样本，因此不满足独立性，该条件满足。

条件3：观察变量不存在显著的异常值，该条件需要通过软件分析后判断。

条件4：各水平(时间点)观察变量为正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件5：各重复测量水平观察变量的协方差相等，即满足球形假设，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

import pandas as pd #导入pandas包
df = pd.read_csv('单因素重复测量方差分析.csv')
df #查看数据

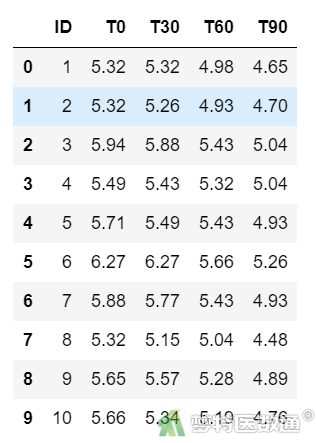
图1

在数据栏目中可以查看数据情况(图1)，在数据集中共有5个变量和10个观察数据，5个变量分别代表10个人的编号(ID)、放置0分钟(T0)、30分钟(T30)、60分钟(T60)和90分钟(T90)。

(二) 适用条件判断

1. 条件3判断(异常值判断)

(1) 软件操作

## 描述数据基本情况 ##

df.describe()  #计算基本统计量

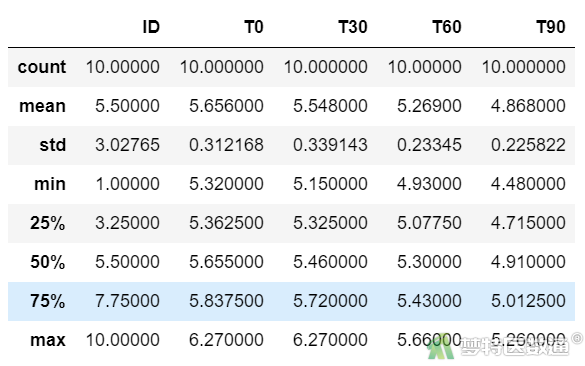
图2

## 分组绘制箱线图 ##

import matplotlib.pyplot as plt
plt.boxplot((df.T0,df.T30,df.T60,df.T90),labels=('T0','T30','T60','T90'),vert = True)
plt.show()

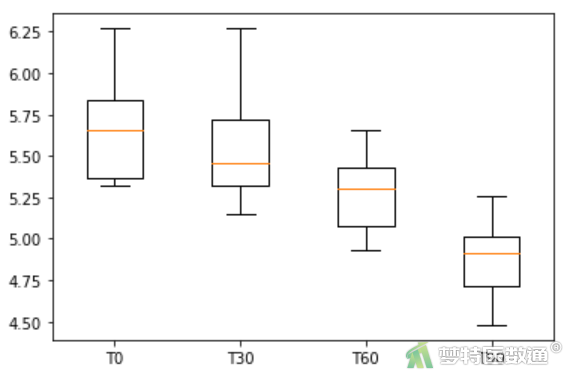
图3

(2) 结果解读

“describe (描述性分析)”命令运行结果(图2)，列出了观察变量的“mean (均数)”、“std (标准差)”、“min (最小值)”、“25% (下四分位数)”、“50% (中位数)”、“75% (上四分位数)”和“max (最大值)”，依据专业尚不能认为存在异常值的情况；此外，箱线图(图3)也未提示任何异常值。综上，本案例未发现需要处理的异常值，满足条件3。

2. 条件4判断(正态性检验)

(1) 软件操作

## 绘制Q-Q图 ##

import statsmodels.api as sm
import pylab
sm.qqplot(df.T0, line='s')  #绘制T0组的Q-Q图
pylab.show()

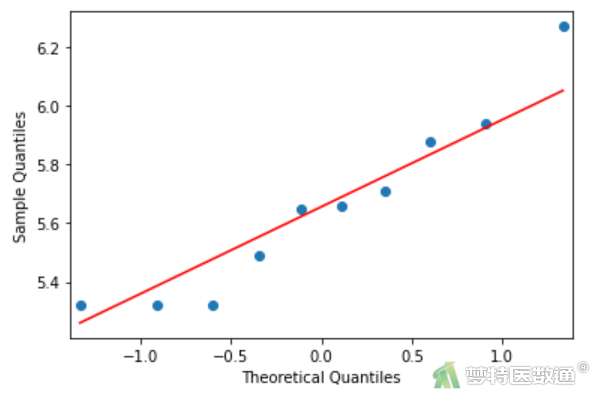
图4-1

sm.qqplot(df.T30, line='s') #绘制T30组的Q-Q图
pylab.show()

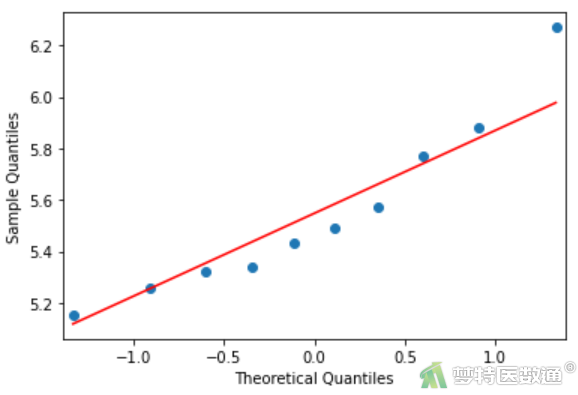
图4-2

sm.qqplot(df.T60, line='s') #绘制T60组的Q-Q图
pylab.show()

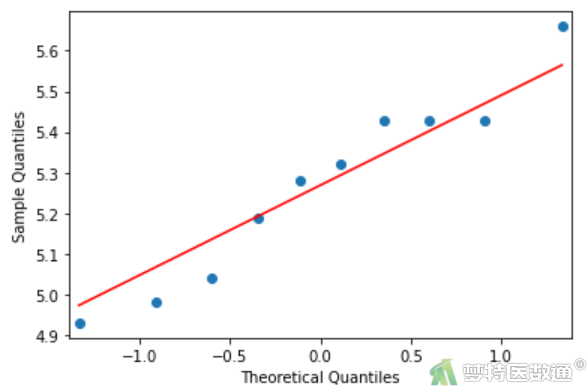
图4-3

sm.qqplot(df.T90, line='s') #绘制T90组的Q-Q图
pylab.show()

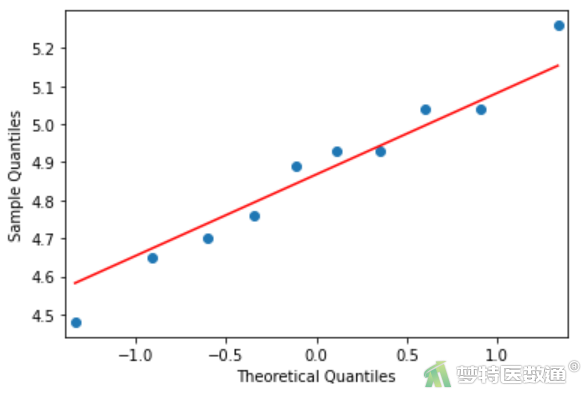
图4-4

## 正态性检验 ##

from scipy import stats
shapiro_test1 = stats.shapiro(df.T0) #检验T0的正态性
print(shapiro_test1)
shapiro_test2 = stats.shapiro(df.T30) #检验T30的正态性
print(shapiro_test2)
shapiro_test3 = stats.shapiro(df.T60) #检验T60的正态性
print(shapiro_test3)
shapiro_test4 = stats.shapiro(df.T90) #检验T90的正态性
print(shapiro_test4)

图5

(2) 结果解读

Q-Q图(图4-1~图4-4)分别显示各组(T0、T30、T60、T90)的数据基本服从正态性；同时，各组数据正态性检验结果(图5)显示，P值分别为0.3269、0.3229、0.6325、0.9724，均>0.1，提示四组数据均服从正态分布。综上，本案例满足条件4。

3. 条件5判断(球形假设检验)

(1) 软件操作

## 球形检验 ##

df2 = df.melt(id_vars=['ID']) #将宽数据转化为长数据
df2

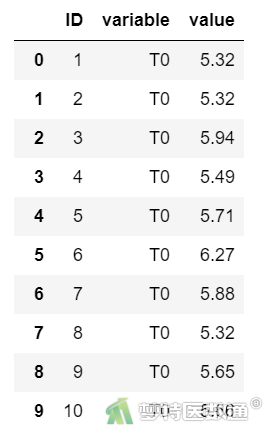
图6

import pingouin
pingouin.sphericity(df2,dv='value',within='variable',subject='ID',method='mauchly') #球形检验

图7

(2) 结果解读

“SpherResults (球形度检验)”结果(图7)显示，W=0.252，P=0.061，>0.05，满足条件5。因此，本案例可以直接采用非校正方法分析的结果。

(三) 统计学推断

1. 软件操作

## 重复测量的方差分析 ##

from statsmodels.stats.anova import AnovaRM
print(AnovaRM(data=df2, depvar='value', subject='ID', within=['variable']).fit()) #重复测量方差分析

图8

2. 结果解读

重复测量方差分析结果(图8)显示，非校正法分析自由度为3，F=116.1027，P<0.001；提示不同时间点该生化指标浓度差异有统计学意义。

(四) 事后检验(两两比较)

上面分析得出了“不同时间点生化指标浓度差异有统计学意义”的结论，但是到底是哪些组别之间存在差异尚不清楚，因此需要进行事后检验，开展两两比较。

1. 软件操作

## 事后检验 ##

from statsmodels.stats.multicomp import pairwise_tukeyhsd,tukeyhsd,MultiComparison
print(pairwise_tukeyhsd(df2['value'], df2['variable'])) #事后两两比较

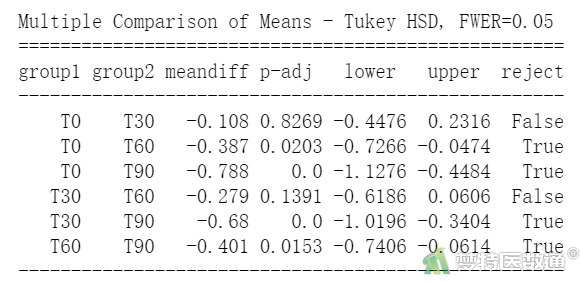
图9

2. 结果解读

“TukeyHSD (事后检验比较)”结果(图9)显示了各组两两比较的“meandiff (均数差)”、“lower (95%置信区间下限)”、“upper (95%置信区间上限)”和“p-adj (调整后的P值)”。可知，随着时间的延长，T90及T60时刻与T0时刻相比，均值差逐渐增加，差异均有统计学意义(P<0.05)；T60及T30时刻与T90时刻相比，均值差增加，差异均有统计学意义(P<0.05)。

四、结论

本研究采用单因素重复测量方差分析判断四个时间点的生化指标浓度是否有差异。通过专业知识判断，数据不存在异常值；通过Shapiro-Wilk检验，提示各组数据服从正态分布；球形度检验提示满足球形假设(W=0.252，P=0.061)，使用未校正法进行数据分析。

各时间点(T0、T30、T60、T90)的生化指标浓度均值分别为5.66±0.31、5.55±0.34、5.27±0.23、4.87±0.23 mmol/L。分析提示，不同时间点生化指标浓度差异有统计学意义(F=116.1，P<0.001)。进一步进行两两比较(TukeyHSD法)，可知随着时间的延长，T90及T60时刻与T0时刻相比，均值差逐渐增大，且均有统计学意义(P<0.05)；T60及T30时刻与T90时刻相比，均值差增加，差异均有统计学意义(P<0.05)。综上可知，放置时间对该生化指标检测结果具有较大的影响。

五、知识小贴士

重复测量设计常见于同一组研究对象多次、多个部位或多个维度测量数据间的比较，包括时间重复测量、部位重复测量和维度重复测量。时间重复测量如，同一组患者用药后多个时间点某疗效指标的比较；部位重复测量如，相同研究对象，身体多个部位某指标(如皮质厚度)的比较；维度重复测量如，使用某量表测量同一批研究对象不同生理或心理状态，其不同状态维度之间的比较(如生活质量SF-36量表各个维度之间的比较)。

六、分析小技巧

(一) 球形度检验

重复测量数据的方差分析过程中，需要先考察数据的球形分布特征，当违背了球形假设条件时，需要进行epsilon (ε)校正。epsilon (ε)值越低，说明违反球形假设的程度越大，当epsilon (ε)=1时，完全服从球形假设。当Greenhouse-Geisserepsilonε<0.75时，使用Greenhouse-Geisser方法校正；当Greenhouse-Geisserepsilonε>0.75时，使用Huynh-Feldt方法校正。

(二) 基线数据处理

重复测量数据分析往往会遇到基线数据和后续测量数据的条件不一致的情况，如针对某种治疗方法对镇痛效果的影响，测量了治疗前和治疗后多次时间点的镇痛效果，此时基线数据和后续多个测量数据的条件则不一致。对于这种情况，基线数据一般不应作为重复测量的第一次纳入重复测量方差分析。