单样本Wilcoxon符号秩检验(One Sample Wilcoxon Signed Rank Test)——Python软件实现

关键词：Python软件; 非参数检验; 秩和检验; 单样本Wilcoxon符号秩检验; 单样本秩和检验

一、案例介绍

某地正常人尿氟含量的中位数为45.20 μmol/L。今在该地某厂随机抽取12名工人，测得尿氟含量。问该厂工人的尿氟含量是否与当地正常人的尿氟含量有差异？数据见图1。本案例数据可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较样本的水平是否与已知的总体中位数有差异，属于单样本设计的假设检验范畴。计量资料的单样本设计假设检验，主要有单样本t检验和单样本Wilcoxon符号秩检验。对于计量资料，若不满足正态性或数据分布情况未知以及一端或两端是不确定数值时，选用秩转换的非参数检验更为恰当。

对于本案例，首先进行正态性检验，若发现不服从正态分布，则选用单样本Wilcoxon符号秩检验。

三、软件操作及结果解读

(一) 导入数据

import pandas as pd #导入pandas包
df = pd.read_csv('单样本Wilcoxon符号秩检验.csv')  #导入CSV数据
pd.set_option('display.max_rows', 10)
df  #查看数据

图1

在数据栏目中可以查看全部数据情况(图1)，数据集中共有2个变量和12个观察数据，2个变量分别代表被调查者的编号(ID)及其对应的尿氟含量(F)。

(二) 适用条件判断

1. 异常值判断

(1) 软件操作

##查看最大值和最小值##

df.F.describe() #F描述性统计分析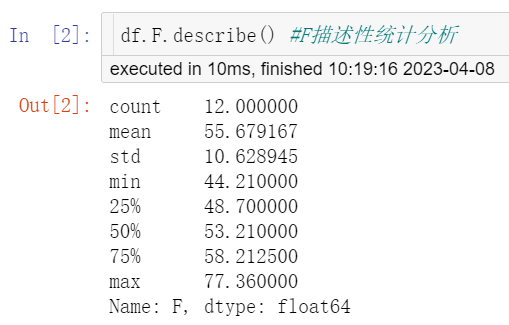

图2

##绘制F的箱线图##

import matplotlib.pyplot as plt
plt.boxplot((df.F),labels=('F'),vert = True) #绘制箱式图
plt.show()

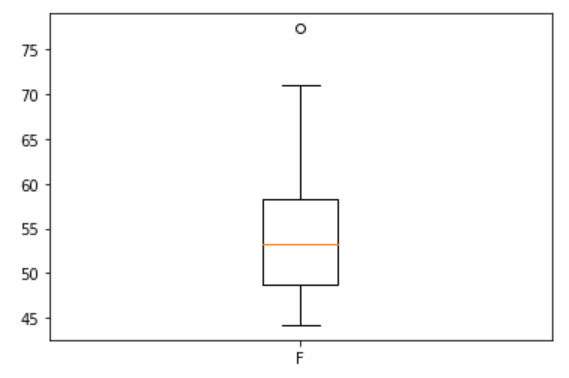
图3

(2) 结果解读

“describe (描述性分析)”命令运行结果 (图2) 列出了观察变量的“mean (平均值)”、“std (标准差)”、“min (最小值)”、“25%(下四分位数)”、“50% (中位数)”、 “75% (上四分位数)”和“max (最大值)”，依据专业可判断尿氟含量均可能存在44.21μmol/L和77.36 μmol/L的情况；此外，箱线图也未提示任何异常值 (图3)。综上，本案例未发现需要特殊处理的异常值。

2. 正态性检验

(1) 软件操作

## 绘制Q-Q图##

import statsmodels.api as sm
import pylab
sm.qqplot(df.F, line='s')
pylab.show()

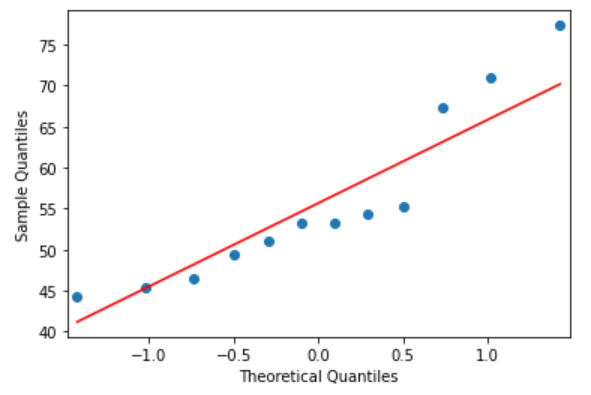
图4

##正态性检验##

from scipy.stats import shapiro
shapiro(df.F) # shapiro-Wilk正态性检验

图5

(2) 结果解读

Q-Q图上散点与对角线的分布重合度较低(图4)，提示数据不服从正态分布；“Shapiro-Wilk normality test (S-W正态性检验)”结果显示P=0.06188<0.1 (图5)，也提示数据不服从正态分布。综上，本案例宜选用单样本Wilcoxon符号秩检验。关于正态性检验的注意事项详见 (正态性假设检验(Normality Hypothesis Test)——SPSS软件实现)(链接)。

(三) 统计描述及推断

1. 软件操作

##Wilcoxon检验##

y=[45.20]*len(df.F)
from scipy import stats
stats.wilcoxon(df.F,y) #对比中位数为45.20

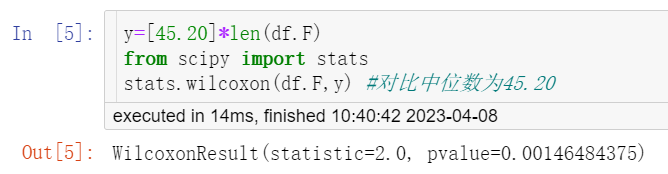
图6

2. 结果解读

Wilcoxon符号秩检验结果 (图6) 显示P = 0.00146，可以认为该厂工人尿氟含量与当地正常人尿氟含量水平之间的差异有统计学意义 (P<0.05)。

四、结论

本案例欲比较某厂工人的尿氟含量与当地正常人的尿氟含量水平是否存在差异，对该厂工人的尿氟含量进行正态性检验发现不服从正态分布，故选用单样本Wilcoxon符号秩检验。

经分析，该厂工人的尿氟含量为53.21 (P₂₅~P₇₅：48.70~58.21) μmol/L。采用单样本Wilcoxon符号秩检验分析显示：P = 0.00146，差异有统计学意义 (P<0.05)。本案例结果提示该厂工人的尿氟含量高于当地正常人的尿氟含量水平。