在因子分析过程中,探索性因子分析(exploratory factor analysis, EFA)主要是为了初步找出因子个数以及因子下各个观测变量的组成、相关程度,以进一步为改进因子结构提供依据。而验证性因子分析(confirmatory factor analysis, CFA)则主要用于测量因子维度与条目之间的对应关系是否与研究者预期保持一致,主要用于验证对应关系。本篇文章将实例演示在SPSS软件中进行验证性因子分析的操作步骤。
关键词:jamovi; 主成分分析; 探索性因子分析; 验证性因子分析; 多元统计分析
验证性因子分析(confirmatory factor analysis, CFA)主要用于测量因子维度与条目之间的对应关系是否与研究者预期保持一致。与CFA相对应的为探索性因子分析(e xploratory factor analysis, EFA),二者的区别在于:CFA用于验证对应关系,而EFA用于探索这种对应关系。如果是成熟的量表,研究者可同时使用CFA和EFA分析验证量表的效度。如果量表的权威性较弱,通常使用EFA进行分析。
一、案例介绍
有一份调查了242名研究对象的量表数据,该量表的维度已经通过初步测试和EFA,其共由4个因子表示,第一个因子共4项,分别是A1~A4;第二项因子共5项,分别是B1~B5;第三个因子共5项,分别是C1~C5;第4个因子共5项,分别是D1~D5。现验证此量表的聚合效度和区分效度,并且希望进行共同方法偏差分析。部分数据见图1,本案例数据可从“附件下载”处下载。
二、问题分析
由于本研究的量表是一个已经通过初步测试的量表,并已形成了对应的维度和条目,因此分析时最好选用CFA。但需要满足4个条件:
条件1:数据是以量表形式进行呈现,对于非量表类数据不合适。本研究是一个初步量表,并设置了相应维度和对应的条目,该条件满足。
条件2:样本例数>分析条目数的5~10倍,总样本通常不低于100。本研究19个条目,其10倍数量为190,总样本242满足该条件。
条件3:量表数据已经通过了初步测试,并形成了相应的专业维度和条目。该条件满足。
三、分析步骤
(一) 模型构建
将因子(潜变量)与条目(显变量)对应关系放置规范;此步骤需要注意的是,在进行CFA分析前需要进行EFA分析,首先清理掉对应关系出现严重偏差的条目。
(二) 聚合(收敛)效度分析
1. 专业判断
如果因子与条目间的对应关系出现严重偏差,此时可考虑删除该条目。
2. 载荷系数判断
因子载荷系数值表示因子和条目之间的关联关系,一般查看标准载荷系数值。某条目与因子间的载荷系数值过低(比如<0.7),说明该条目与因子间关系较弱,需要删除该条目。
3. 修正指数判断
修正指数(modification indices,MI)表示两项间的关联强度,MI值越大说明两项间的关联性越强,如果两项之间的关联性过强会干扰模型,导致模型拟合指标不佳,对于MI值过大,如果>10或者>15可考虑删除条目,对于稍微偏高的MI值条目,可考虑建立关联关系,进行微调。
4. 平均方差提取值和组合信度
平均方差提取值(average variance extracted,AVE)是因子包含条目的方差量的量度,与测量误差引起的方差量有关。AVE值>0.5,组合信度(composite reliability,CR)值>0.7,说明测量量表数据具有优秀的聚合效度。
5. 因子协方差
因子协方差可展示因子与因子之间的关联性,可通过标准系数进行分析。
6. 其他判断指标
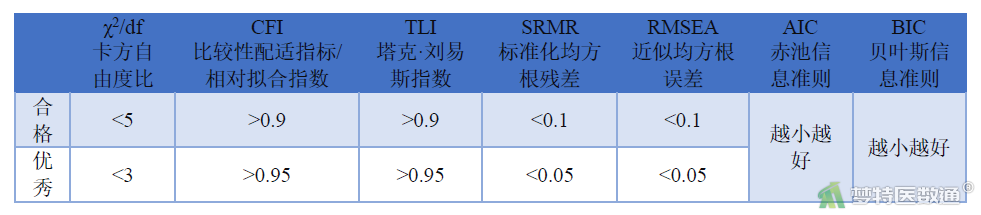
其他拟合指标判断标准见表1。
(三) 区分效度分析
区分效度的测量是使用AVE的平方根值,然后与各个因子的相关系数进行对比,如果AVE平方根值大于“该因子与其它因子间的相关系数”,说明具有良好的区分效度。AVE平方根值可表示该因子的“聚合性”,而相关系数表示相关关系,如果该因子自己“聚合性”很强(明显强于与其它因子间的相关系数),则能说明具有较好区分效度。
区分效度首先需要进行相关分析(因为每个因子对应多个条目,可将因子内的各个条目得分平均,将其概括成一个整体变量后再进行两两相关分析)。
(四) 共同方法偏差
共同方法偏差(common method variance,CMV)常见有两种验证方式,一种是使用EFA分析进行检验(也称作“Harman单因子检验方法”),即把所有条目进行EFA分析时,如果只得出一个因子或者第一个因子的解释力(方差解释率)特别大,通常以50%为界,此时可判定存在共同方法偏差(同源方差),反之说明没有共同方法偏差问题。另一种则是使用CFA分析进行验证,将所有因子对应的条目放在一个因子里面,然后进行分析,如果测量出来显示模型的拟合指标(χ2/df、RMSEA、RMR、CFI等)无法达标,则说明模型拟合不佳,即表示所有条目不应同属于一个因子,因而说明数据不存在共同方法偏差问题。
在量表效度分析过程中,CFA通常有三个用途:一是通过聚合(收敛)效度分析,检验本应在同一因子下的条目,是否确实在同一因子下,主要查看AVE、 CR和因子载荷 (factor loading);二是通过区分效度分析检验本不应在同一因子下的条目,确实不在同一因子下,主要对比AVE的根号值和相关系数;三是通过CMV,也称同源方法分析,检验量表数据是否需要产生多个因子,常采用Harman单因子检验方法(Harman's Single-Factor Test,通过EFA分析实现)或CFA单个因子分析的拟合效果判断。
四、软件操作及结果解读
(一) 模型构建
选择“分析”—“因子”—“验证性因子分析”(图2);
将“A1~A4”选入“因子1”框(图3),点击“添加新的因子”;同理,将“B1~B5”选入“因子2”框,将“C1~C5”选入“因子3”,将“D1~D5”选入“因子4”框。
(二) 聚合(收敛)效度分析
1. 专业判断
如果因子与条目间的对应关系出现严重偏差,此时可考虑删除某条目,此步骤主要在EFA过程完成。
2. 载荷系数判断
(1) 软件操作
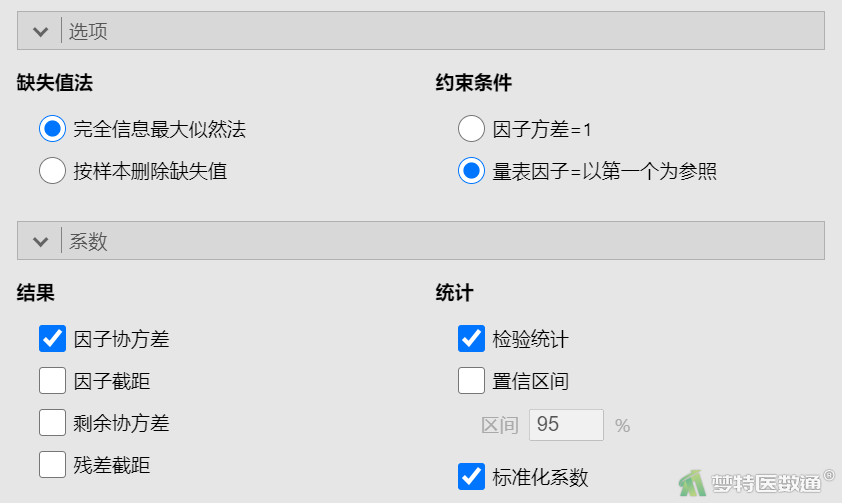
在“选项”下的“缺失值法”中选中“完全信息最大似然法”;在“约束条件”中选中“量表因子=以第一个为参照”;在“系数”下的“结果”中勾选“因子协方差”,在“统计”中勾选“检验统计”和“标准化系数”(图4)。

(2) 结果解读
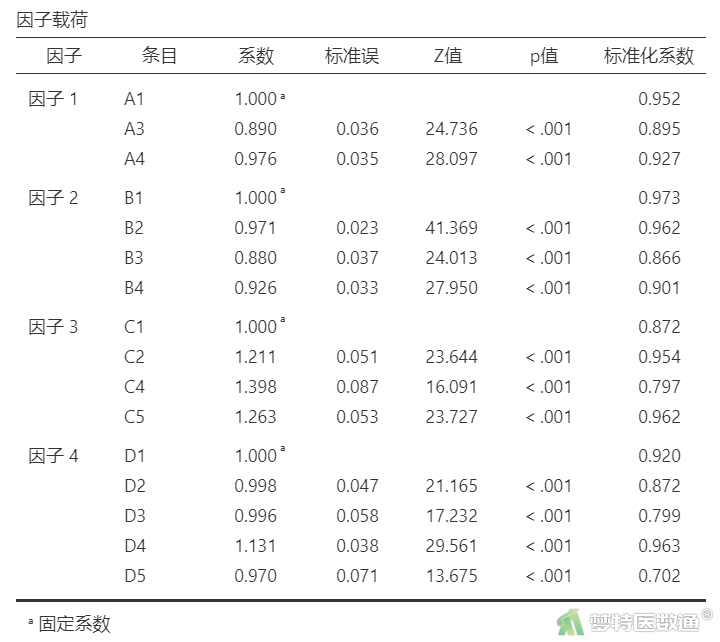
“因子载荷”结果(表2)表明,条目C3在因子3下的“标准化系数”为0.582 < 0.7,说明对应关系较弱,可考虑将此项从因子3中移除。
另外从整体上看,各个条目均呈现出0.001水平的显著性(P<0.001),而且标准载荷系数值均大于0.7(除C3外),说明整体上因子与条目之间有着良好的对应关系,聚合效度较好。
3. 修正指数判断
(1) 软件操作
将C3从因子3中移除,再次分析。在“附加输出结果”下的“事后模型性能”中勾选“修正指数”,在“突出显示高于此值的结果”中填写“15”(图5),结果见表3。
(2) 结果解读
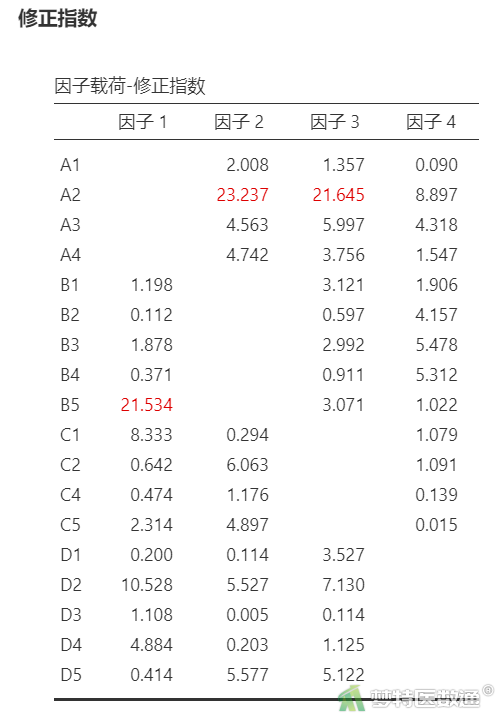
“因子载荷-修正指数”结果(表3)展示了因子与条目的对应关系的MI值,可见A与因子2、因子3两个因子间的MI指标均大于15,说明A2与因子2、因子3之间可能有着较强的关联性;同时,B5与因子1之间的MI值为21.532,说明二者有较强的关联性。综合可知,可考虑将A2、B5这两个指标从模型中移除。
如果不希望对MI值较大的条目进行删除(如从专业角度来看该条目必须保留,或者该因子下所剩条目不多时),可将该条目选入MI值较大的因子下进行微调(如本案例中将A2选入“因子2”下,将B5选入“因子1”下),此时可解决MI值过大的问题,并且模型各项拟合指标会有所改善。但这种处理措施也存在一定问题,一是会导致标准因子载荷系数出现改变(如<0.7),甚至异常(如>1);二是很多情况下并不会显著提升模型的拟合指标(以上过程请感兴趣的作者自行操作)。因此,对于MI值较大的条目,最根本的处理措施应该是删除不合理的对应关系,找出因子与条目的真实对应关系,才能建立合理的CFA模型。
4. 平均方差提取值和组合信度
(1) 软件操作
将A2、B5从因子2和因子1中移除,再次分析,结果见表4。
使用λ代表条目的标准载荷系数,那么AVE和CR的计算公式分别为:
\(\mathrm{AVE}=\frac{\sum \lambda^{2}}{\left[\sum \lambda^{2}+\sum\left(1-\lambda^{2}\right)\right]}\)
\(\mathrm{CR}=\frac{\left(\sum \lambda\right)^{2}}{\left[\left(\sum \lambda\right)^{2}+\sum\left(1-\lambda^{2}\right)\right]}\)
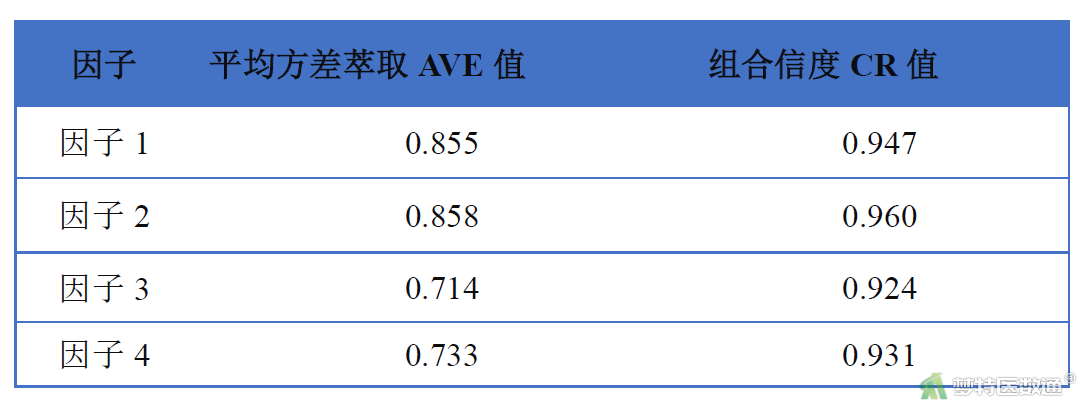
“因子载荷”结果(表4)显示,每个因子内各条目的“标准化系数”按照上述计算公式,可计算AVE值和CR值,结果见表5。
(2) 结果解读
本次研究量表共由四个因子表示(表5),对应的AVE值全部均大于0.7,最小是0.714,明显高于0.5这一标准;而且组合信度CR值均大于0.9,明显高于0.7这一标准。因而说明本次研究量表具有优秀的聚合效度。
如果AVE和CR值较低,可尝试以下解决方案:
按照标准因子载荷系数从低至高的顺序,逐步依次移除载荷系数值较低的条目;
逐步依次移除修正指数较高的条目;
加大样本量,一般情况下样本量越大模型拟合效果越佳。
5. 因子协方差
(1) 软件操作
在“系数”下“结果”中勾选“因子协方差”(图4)。
(2) 结果解读
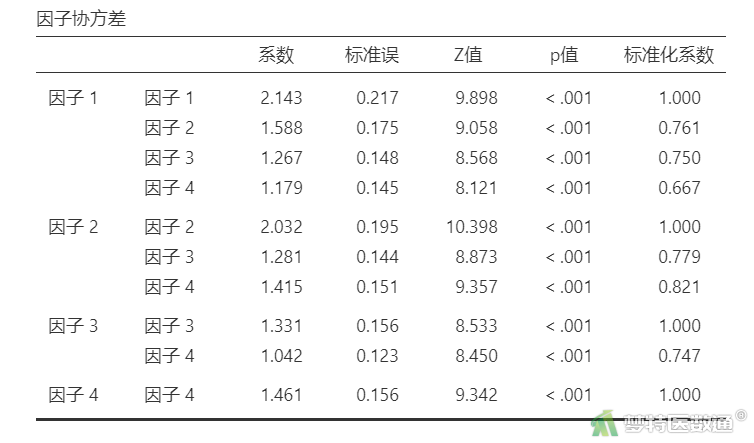
“因子协方差”结果(表6)显示,“标准化系数”展示了因子与因子之间的关联性。可知,本研究4个因子两两之间的标准系数值介于0.667~0.821之间,说明因子之间具有较强的关联性。
6. 其他判断指标
(1) 软件操作
在“模型拟合”中勾选所有选项(图6),结果见表7、表8。

(2) 结果解读
“精确拟合检验”结果(表7)显示,χ²=493.095,P<0.001,提示模型拟合较差。但是CFA分析过程中的卡方检验对样本量非常敏感,当样本量较大时,尽管模型拟合较好往往也会出现P<0.05的情况,因此需要结合其他指标进行综合判断。

“拟合评价”结果(表8)显示,相对拟合指数(CFI)=0.921>0.9,为合格;TLI指数=0.904>0.9,为合格;标准化均方根残差(SRMR)=0.038<0.05,为优秀;近似均方根误差(RMSEA)=0.129>0.1,欠佳;综合可知模型拟合为合格。

(三) 区分效度分析
1. 软件操作
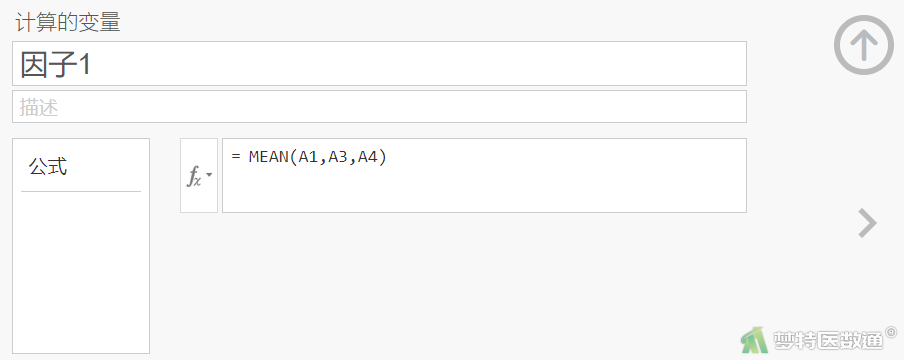
①将各因子下的条目(删除条目不纳入)得分取平均值,生成新的变量,计算各变量的相关系数。如在“计算变量”的“公式”框中输入“= MEAN(A1,A3,A4)”,可得到因子1的数值(图7);依此可计算条目B1、B2、B3、B4的平均值因子2,条目C1、C2、C4、C5的平均值因子3,条目D1、D2、D3、D4、D5的平均值因子4;
②选择“分析”—“回归”—“相关矩阵”,将“因子1”“因子2”“因子3”“因子4” 同时选入右侧框(图8);
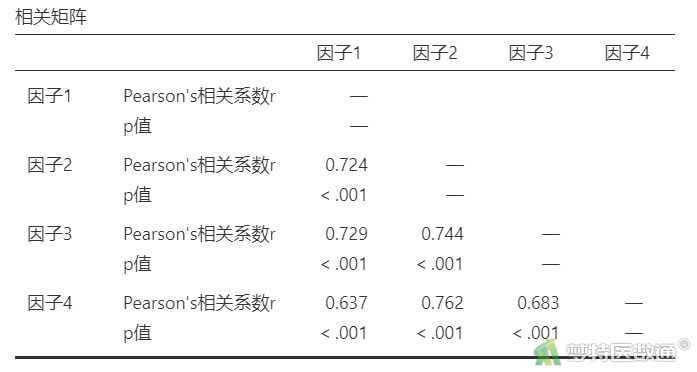
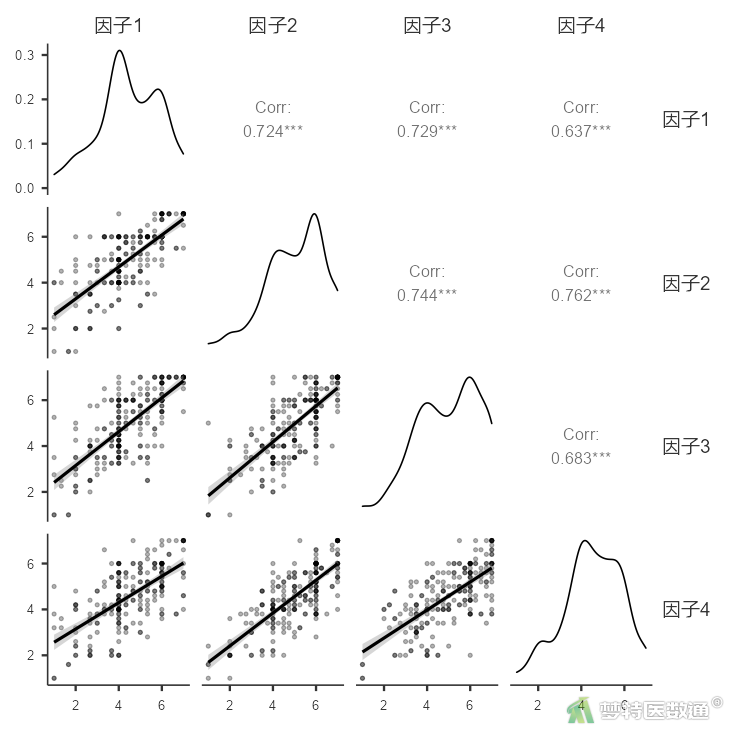
③在“相关系数”中勾选“Pearson系数”,“假设检验”中选则“相关”,“附加选项”中勾选“报告p值”,“图”中勾选“相关矩阵”“变量概率密度”“统计”(图9),结果见表9、图10。
2. 结果解读
区分效度分析时,常会将“相关矩阵”表格(表8)中斜对角线的“—”换成“AVE值的平方根”,然后再进行对比分析,见表10。
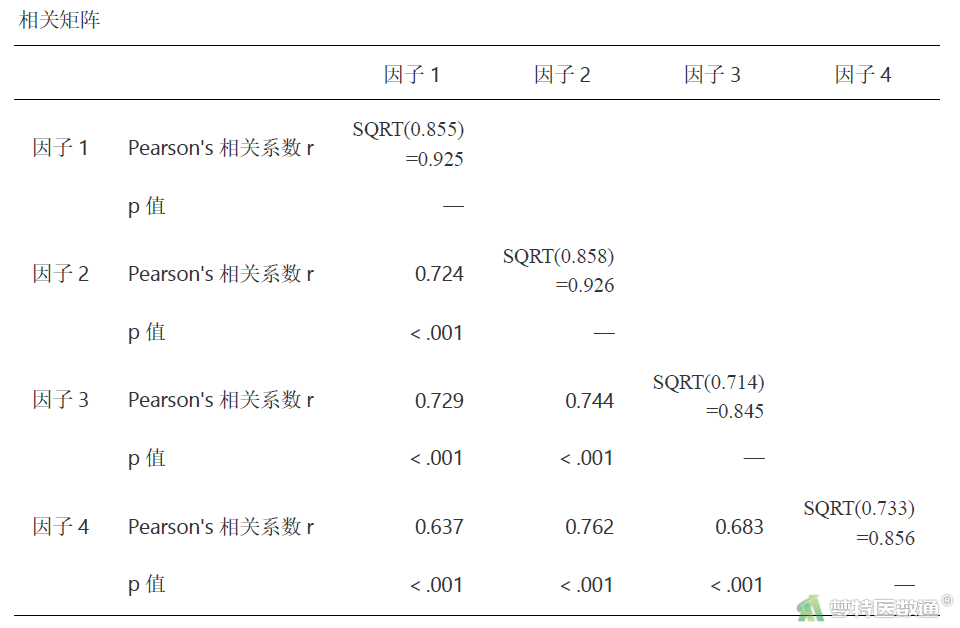
“相关矩阵”结果(表10)显示,因子1的AVE根号值为0.925,大于因子1与另外3个因子之间的相关系数值(最大为0.729);因子2的AVE根号值为0.926,大于因子2与另外3个因子之间的相关系数值(最大为0.762);类似地,因子3与因子4的AVE根号值(0.845和0.856)均大于它们与其它因子的相关系数值。因而说明研究量表数据的区分效度良好。
区分效度不达标,通常是由于出现“错位”现象,比如某因子里面有一个或多个条目放在其他因子里面更适合。一般结合载荷值判断出此类条目,然后进行删除或将其移位即可。
(四) 共同方法偏差(也称同源方法,CMV)
1. 软件操作
①选择“分析”—“因子”—“探索性因子分析”,将需要分析的19个条目选入右侧“变量”框(图11);
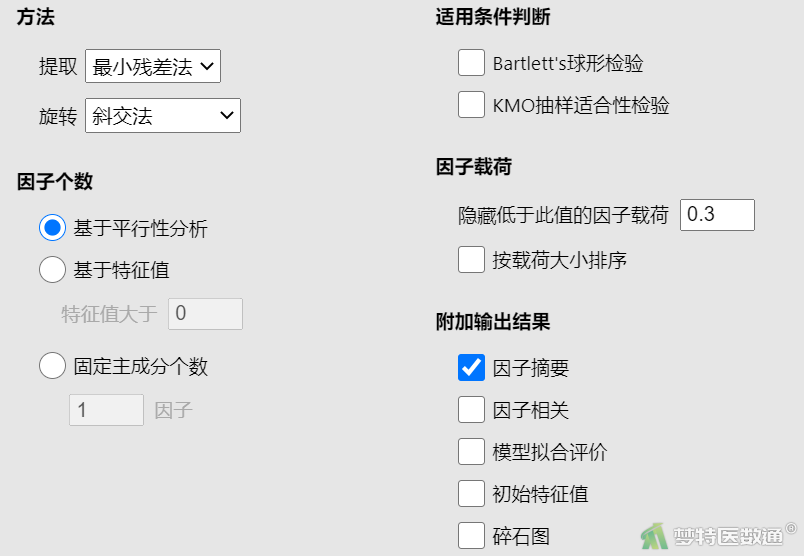
②在“因子个数”中选择“基于平行分析”,在“附加输出结果”中,勾选“因子摘要”(图12),结果见表11。
2. 结果解读
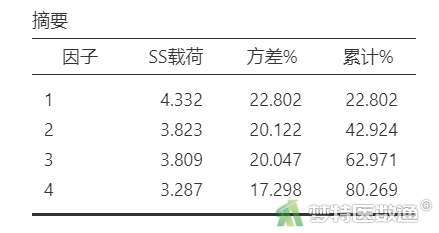
在“摘要”表格(表11)中提取了4个因子,并且没有因子的方差解释率>50%,说明没有共同方法偏差问题。
此外,将所有的条目放在一个因子里面进行CFA分析(感兴趣的读者请自行分析),发现各项拟合指标均较差(表12和表13),也说明所有的条目并不应该同属于一个因子,因此提示没有共同方法偏差问题。


五、结论
本研究通过CFA分析检验量表的聚合效度、区分效度及共同方法偏差问题。
通过载荷系数判断将条目C3从因子3中移除,通过修正指数判断将条目A2、B5分别从因子2和因子1中移除。对剩余的16个条目计算平均方差提取值和组合信度,发现4个因子的AVE值全部均大于0.7,CR值均大于0.9。因子协方差分析显示4个因子两两之间的标准系数值介于0.667~0.821之间。模型拟合指标显示,CFI=0.921,TLI=0.904,SRMR=0.038,RMSEA=0.129,模型拟合为合格。因此,本量表具有较好的聚合效度。所有因子的AVE根号值均大于它们与其它因子的相关系数值,因而说明研究量表数据的区分效度良好。对所有条目进行EFA,可提取4个因子,并且没有因子的方差解释率>50%;将所有条目放在一个因子里面进行验证性因子分析,发现各项拟合指标均较差,因而说明没有共同方法偏差问题。综上,本研究量表数据具有较好的聚合效度和区分效度,不存在共同方法偏差问题。
六、分析小技巧
- 如果是非经典量表,通常情况下研究人员会使用EFA分析进行效度验证,该验证方法一般称作结构效度分析;同时还会使用内容效度进行分析,即用文字描述量表的来源设计过程等,用于论证研究量表的有效性。当然如果还想进一步分析,亦可使用CFA进行深入研究。
- 如果是经典量表需要进行效度验证,其内容效度确认无疑,而且使用EFA进行分析时,也具有良好的结构效度。所以研究人员更偏好于使用CFA进行深入分析,即进行聚合(收敛)效度和区分效度分析。
- 如果使用CFA进行聚合(收敛)效度,或区分效度分析,建议首先进行EFA分析,然后再进行CFA分析;原因在于CFA对于数据质量要求高,如果EFA分析就发现因子与条目对应关系出现偏差,需要首先进行处理,确认好因子与条目对应关系后,再进行CFA分析。