Kaplan-Meier生存分析(Kaplan-Meier Survival Analysis)——Python软件实现

关键词：Python; Kaplan-Meier生存分析; 生存分析; KM生存分析; Log-rank检验; 生存曲线

一、案例介绍

某肿瘤研究中心收集了2010—2015年确诊为宫颈癌的患者生存数据，包括结局(Status：0=删失，1=死亡)、随访时间(Time，月)和组织学分级(Hist_stage：1=原位癌，2=早期浸润癌，3=浸润癌)，部分数据见图1，欲探究不同组织学分级的宫颈癌患者的生存结局有无差异。本案例数据可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较3种组织学等级的宫颈癌患者的生存结局有无差异，可以采用Kaplan-Meier生存分析。但需要满足4个条件：

条件1：结局为互斥的二分类变量。本案例结局变量为删失和死亡，是互斥的二分类变量，该条件满足。

条件2：随访时间或生存时间定义明确，并为量化数据，即以天、周、月、年等为单位的具体数值。本案例数据的生存时间为准确可测量的月数，该条件满足。

条件3：不宜有长期变异存在。对于动态队列，研究对象不是同时进入队列的，那么如果后期进入队列的研究对象使用了新的治疗方案和药物，生存率提高，那么整个队列的生存结果就会发生偏倚。该条件需要根据实际情况来判断，这里默认无长期变异。

条件4：删失事件在各组的分布相似。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

import pandas as pd
df = pd.read_csv(r'Kaplan-Meier生存分析.csv')   #导入CSV数据
df

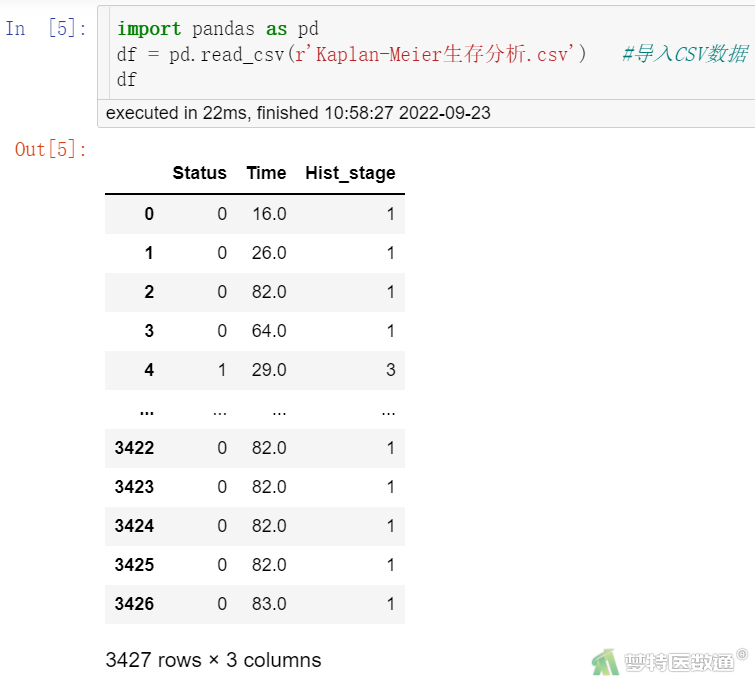
在数据栏目(图1)中可以查看全部数据情况，数据集中共有3个变量和3427例观察数据，3个变量分别为结局(Status：0=删失，1=死亡)、随访时间(Time)和组织学分级(Hist_stage:1=原位癌，2=早期浸润癌，3=浸润癌)。

(二) 条件4判断(删失事件的占比与分布)

1. 软件操作

##生存数据统计##

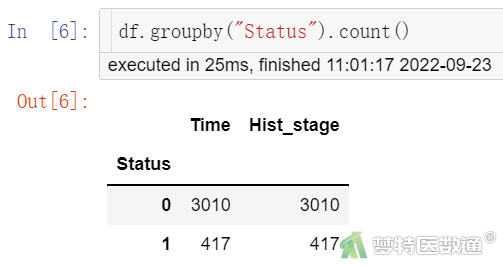
df.groupby("Status").count()

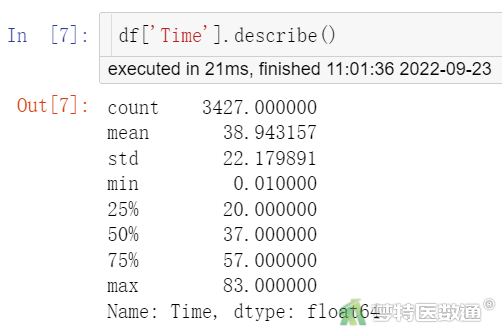
df['Time'].describe()

##筛选结局为删失的患者##

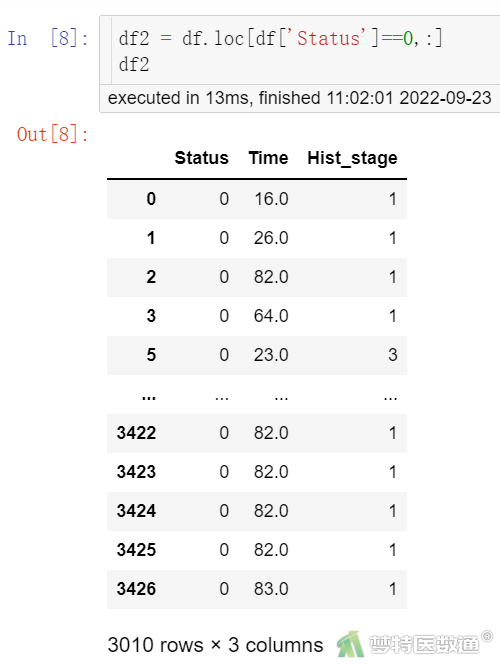
df2 = df.loc[df['Status']==0,:]
df2

##绘制删失数据在不同级别组织中的分布图##

import matplotlib.pyplot as plt
import numpy as np
x = df2.Time 
y = df2.Hist_stage     # 定义数据 
plt.figure(figsize=(8,5))     # 确定画布
plt.xlabel("Time")
plt.ylabel("Hist_stage")
plt.scatter(x,      # 横坐标
            y,      # 纵坐标
            c='green',     # 点的颜色
            s=8,      # 调整点的大小
            label='S')      # 标签即为点代表的意思
plt.legend()     # 显示图例
plt.show()     # 显示所绘图形

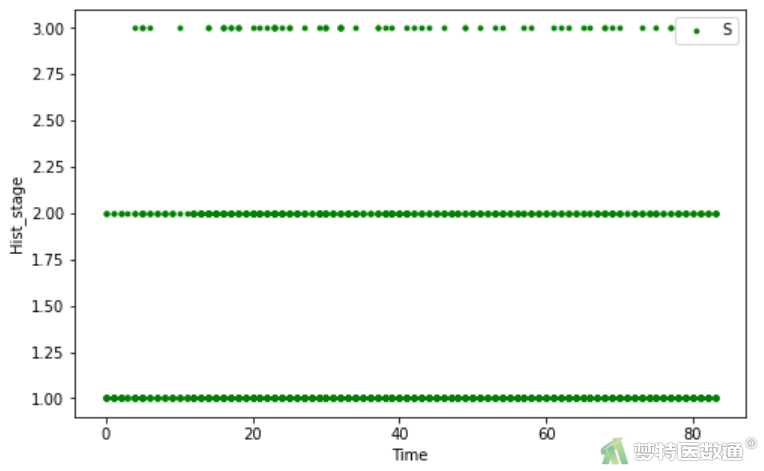
2. 结果解读

由图2~3可知，有417例患者发生终点事件，随访时间最长患者随访了83个月，平均随访时间39个月。筛选结局为删失的患者(图4)后，绘制删失数据在不同级别组织中的分布图(图5)显示，整个随访期间内不同组织学分级组内删失的分布相似，即满足条件4。

(三) 统计学描述及推断

Log-rank检验是比较不同组患者生存曲线的非参数检验，属于单因素分析。若想校正其他因素则需要采用Cox比例风险模型进行分析。

1. 软件操作

##计算每组的中位生存时间##

from lifelines.datasets import load_waltons
from lifelines import KaplanMeierFitter
from lifelines.utils import median_survival_times
##计算中位生存时间##
kmf = KaplanMeierFitter()
for name, grouped_df in df.groupby('Hist_stage'):
    kmf_temp = KaplanMeierFitter()
    kmf_temp.fit(grouped_df["Time"], grouped_df["Status"])
    median = median_survival_times(kmf_temp)
    print(f"{name}组的中位生存时间:{median}")

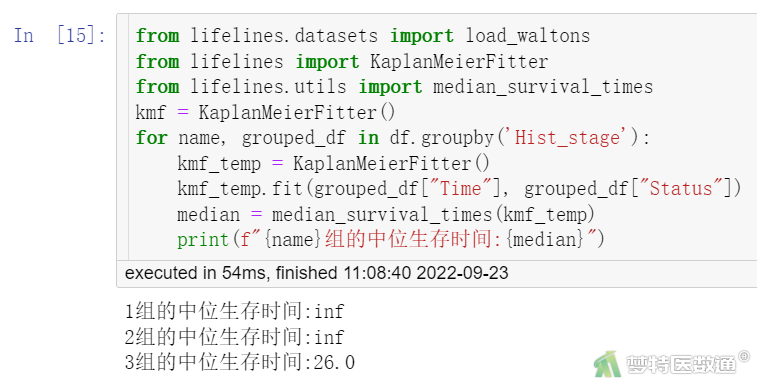
##比较3组的生存曲线差异是否有统计学意义##

from lifelines.statistics import multivariate_logrank_test
kmf = KaplanMeierFitter()
for name, grouped_df in df.groupby('Hist_stage'):
    kmf.fit(grouped_df["Time"], grouped_df["Status"], label=name)
    kmf.plot_survival_function()
results = multivariate_logrank_test(df['Time'], df['Hist_stage'], df['Status'])
results.print_summary()
print(results.p_value)

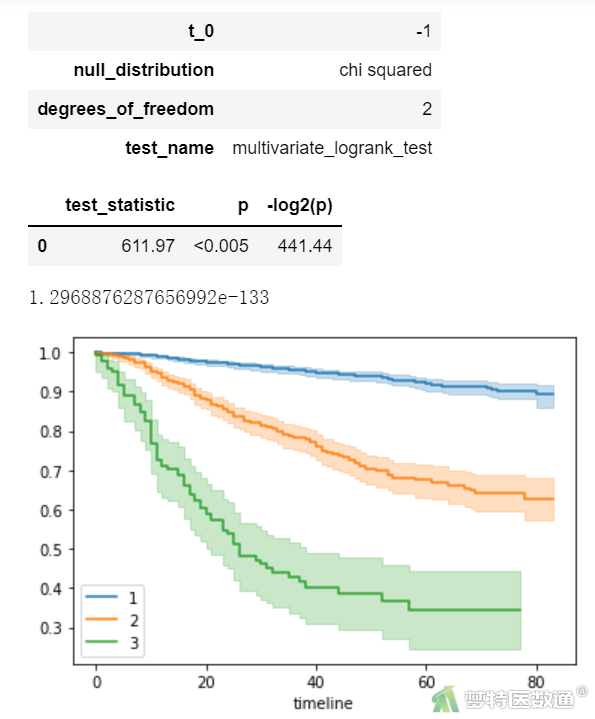
##两两比较##

from itertools import combinations
from lifelines.statistics import logrank_test
from statsmodels.sandbox.stats.multicomp import multipletests
##分别计算1-2,1-3,2-3三组的logrank检验P值##
dict_p = {}
for i in list(combinations(pd.unique(df.Hist_stage),2)):
    logrank = logrank_test(df.loc[df.loc[:,'Hist_stage'].isin(i),"Time"], df.loc[df.loc[:,'Hist_stage'].isin(i),'Hist_stage'], df.loc[df.loc[:,'Hist_stage'].isin(i),'Status'])
    dict_p[str(i)] = logrank.p_value
dict_p

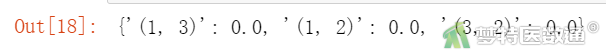
##P值进行矫正##

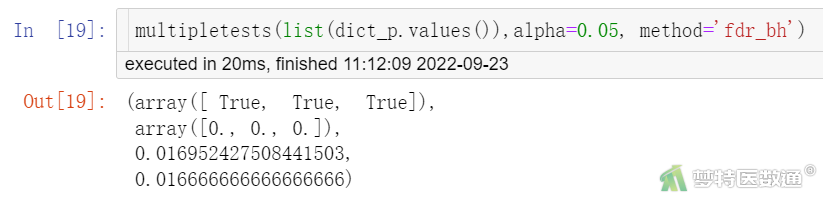
multipletests(list(dict_p.values()),alpha=0.05, method='fdr_bh')

2. 结果解读

统计学描述结果(图6)显示，原位癌(Hist_stage=1)患者和早期浸润癌(Hist_stage=2)患者的中位生存时间没有数值，表示这两组患者的死亡人数尚未达到50%；浸润癌(Hist_stage=3)患者的中位生存时间为26月。log-rank检验的结果以及Kaplan-Meier生存曲线图(图7)显示，不同组织学分级的宫颈癌患者的生存分布差异有统计学意义(χ²=611.97，P<0.005)。Kaplan-Meier生存曲线也表明，3组患者的生存分布有差异，需进行两两比较。两两比较的结果见图8~9，3组患者两两之间的生存分布差异均有统计学意义(True为拒绝原假设)。图9最后两列的检验水准分别为使用sidak法和Bonferroni法校正后的检验水准。可知浸润癌患者的生存概率要低于同一时间段早期浸润癌患者，而早期浸润癌患者低于原位癌患者。

四、结论

本研究采用Kaplan-Meier曲线和log-rank检验对不同组织学分级的宫颈癌患者的生存结果进行比较。不同组织学分级组内删失值分布情况类似。原位癌和早期浸润癌患者的中位生存时间没有数值，表示这两组患者的死亡人数尚未达到50%；浸润癌患者的中位生存时间为26个月。Log-rank检验结果表明不同组织学分级的癌症患者生存分布的差异有统计学意义(χ²=611.97，P<0.005)。进一步进行事后两两比较，结果显示3组宫颈癌患者生存分布差异均有统计学意义(True为拒绝原假设)，原位癌患者生存状况最好，早期浸润癌患者次之，浸润癌患者最差。

五、知识小贴士

(一) 删失数据

在规定的随访期内，未能观察到一些研究对象结局事件的发生，即不能得知结局事件确切的发生时间，称这类研究对象的随访时间/生存时间为删失数据，根据原因可分为3种类型：(1)研究结束时(已达到规定的最长观察期/随访期)，研究对象仍未出现结局事件；(2)由于研究对象在研究期间不再继续就诊，或拒绝访视，或失去联系等，未能观察到结局事件；(3)研究对象出现了竞争事件(如其他原因的死亡)，观察不到既定的结局事件而终止随访。

(二) 中位生存时间

中位生存时间表示累积生存率为50%所对应的时间，是生存分析中最常用的概括性统计量。生存分析中较少使用平均生存时间。

(三) log-rank检验

log-rank检验中的“log”并非“对数”，而是表示count、register或record。在中文描述中可以直接写为“log-rank检验”，或者译为“时序检验”。 log-rank检验是比较不同组患者生存曲线的非参数检验，属于单因素分析。若想校正其他因素则需要采用Cox比例风险模型进行分析。