在SPSS中,对于无序分类资料的组间比较,常选用卡方检验。当数据不满足卡方检验的适用条件时,或者计算出的近似P值接近检验水准界值时,常选用Fisher确切概率法。SPSS输出结果只对四格表默认输出确切概率法的结果,更大的表格则不默认进行该检验方法的计算。这是由于Fisher确切概率法的计算量大、极其耗时,当数据更复杂时,需要很长运行时间,影响操作效率。此时,对于单元格较多,样本量较大的表格我们可选用蒙特卡洛法进行计算。
关键词:SPSS; 蒙特卡洛法; 列联表卡方检验; Fisher确切概率法
蒙特卡洛法是利用给定样本集通过模拟方法重复取样来计算显著性水平,该方法不要求渐进方法中的假设。对于数据不满足渐进假设,或由于计算超负荷而无法得到精确的显著性水平时,可以选择该方法。
一、案例介绍
某研究分析患者年龄和患病类型是否有关联,部分数据见表1。“age”为年龄,赋值为1、2、3、4,分别代表18~25岁、26~30岁、31~40岁、≥41岁。“type”为患病类型,赋值为1、2、3、4、5,分别代表A型、B型、C型、D型、E型。“Frequency”为频数。本案例数据可从“附件下载”处下载。

二、问题分析
本案例的分析目的是比较不同年龄的患病类型构成是否有差异,可以采用R×C χ2检验(渐进法),如果不满足χ2检验(渐进法)适用条件,可以选择Fisher确切概率法,如果Fisher确切概率法耗时太多可以选择蒙特卡洛法。
三、卡方检验(渐进法)
(一) 软件操作
本案例为频数资料,需要先进行加权处理,详细操作详见(个案加权—SPSS实现)。
加权个案后进行卡方检验。
选择“分析”—“描述统计”—“交叉表”(图2)
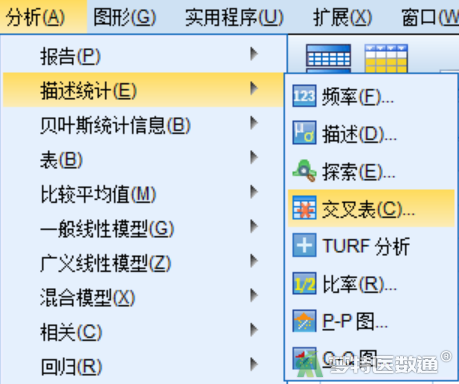
打开“交叉表”对话框,将分组变量“age”放入右侧“行”下方的变量框中,将结果变量“type”放入右侧“列”下方的变量框中(图3),“行”和“列”中的变量可以互换位置,不影响检验结果。
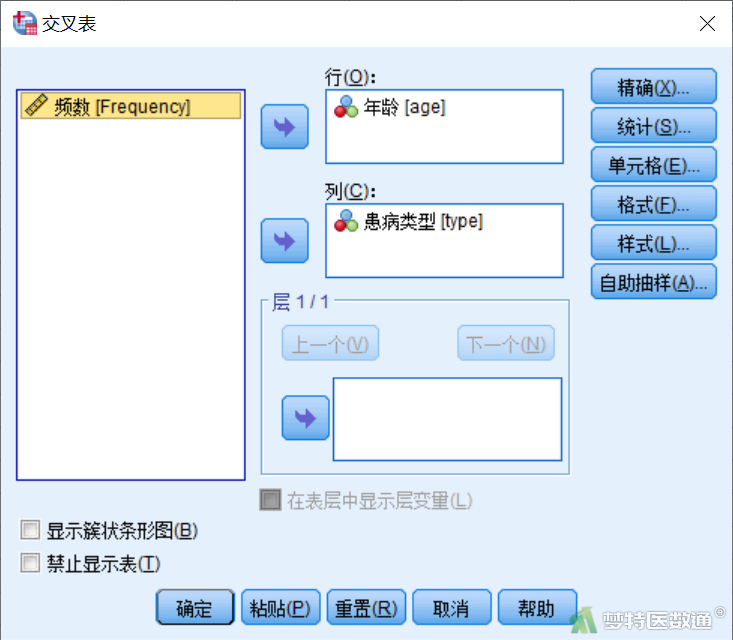
在“精确检验”对话框(图4)中,默认选择“仅渐进法”,点击“继续”回到“交叉表”对话框。
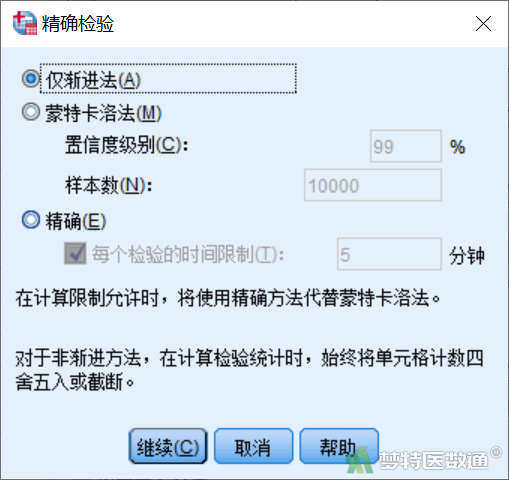
在“交叉表”对话框中点击右侧“统计”,打开“统计”子对话框(图5),勾选“卡方”,点击“继续”,回到“交叉表”对话框。
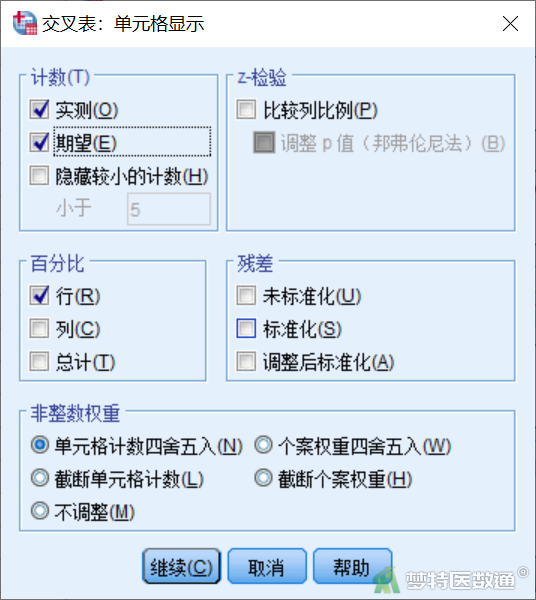
在“交叉表”对话框中点击右侧“单元格”,打开“单元格显示”子对话框(图6),勾选“实测”“期望”和“行”,其他保持默认不变。点击“继续”,回到“交叉表”对话框,点击“确定”即可。
(二) 结果解读
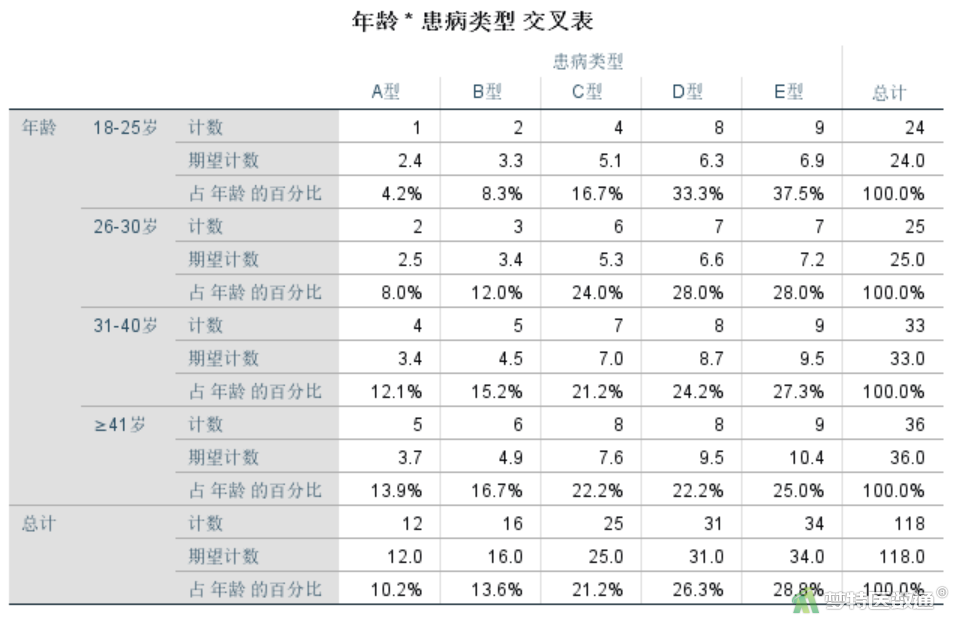
“年龄*患病类型交叉表”结果(图7)给出了不同年龄组不同患病类型的患者观察值、期望频数及组内占比。
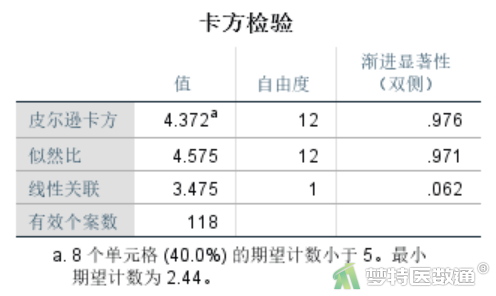
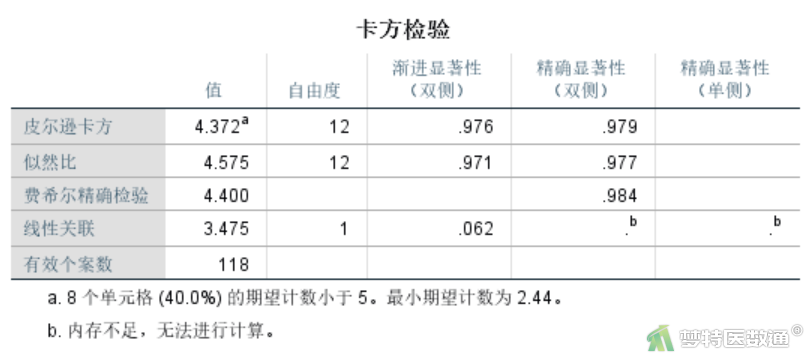
“卡方检验”结果(图8)给出了R×C χ2检验的统计量、自由度和P值。其表格下方显示最小期望频数为2.44,有40%的单元格期望频数<5。因此本案例需要使用Fisher确切概率法。如果使用Pearson χ2检验结果,可知χ2=4.372,P=0.976。即不同年龄组的患病类型构成差异无统计学意义。
四、Fisher确切概率法
(一) 软件操作
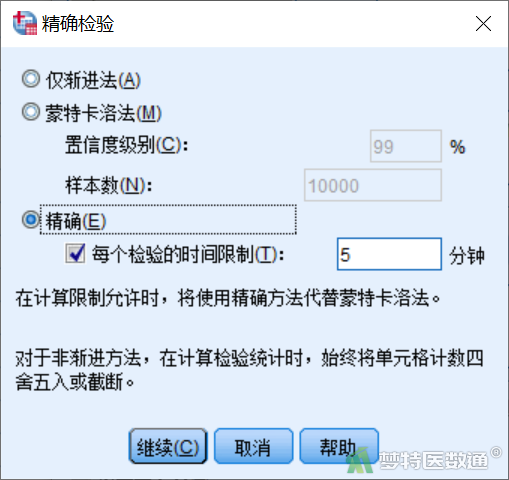
在“精确检验”对话框(图9),选择“精确”,时间限制为“5”分钟。其他操作同渐进法分析。对于本案例单元格较多,因此非常耗时(读者可自行操作)。
(二) 结果解读
Fisher确切概率法检验结果(图10)显示,χ2=4.400,P=0.984。和Pearson χ2检验结果的P值存在一些差异。
五、蒙特卡洛法
(一) 软件操作
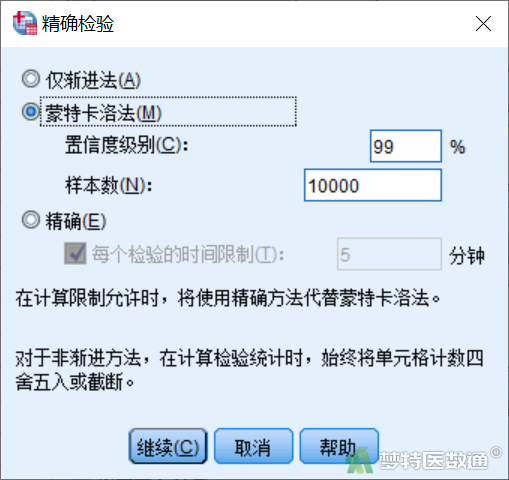
在“精确检验”对话框(图11),选择“蒙特卡洛法”,“置信度级别”和“样本数”保持默认。
(二) 结果解读
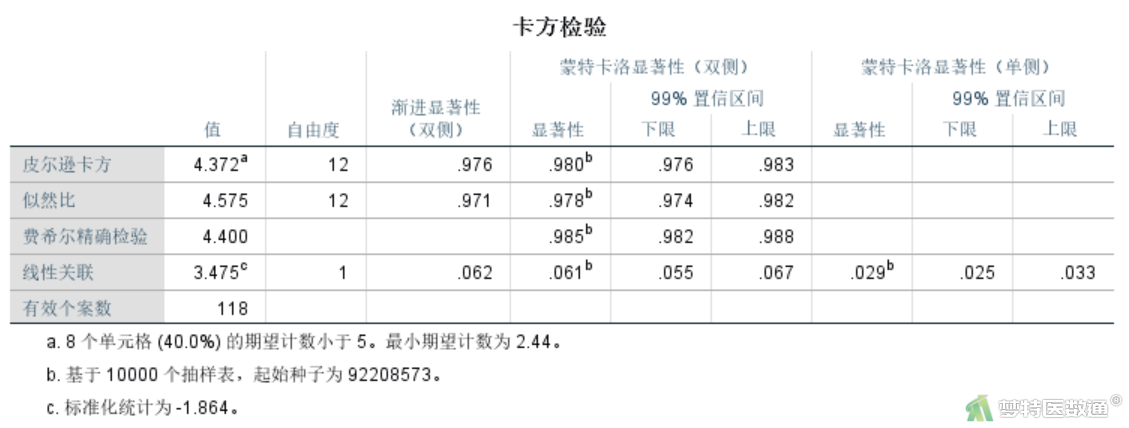
Fisher精确检验一行的蒙特卡洛模拟结果(图12)显示,χ2=4.400,P=0.985。可见和Fisher确切概率法检验结果非常接近。
六、结论
本研究分析患者年龄和患病类型是否有关联,数据不满足Pearson渐进卡方检验的适用条件,采用Fisher确切概率法计算太耗时,遂采用蒙特卡洛法进行分析。
蒙特卡洛法分析结果显示χ2=4.400,P=0.985,表明不同年龄组的患病构成差异无统计学意义。