缺失值填补——期望最大法(EM算法)填补

关键词：缺失值; 缺失值类型; 缺失值填补; EM算法; 复杂填补

一、案例介绍

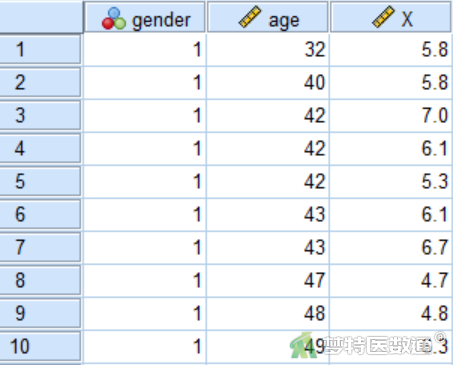
此处仍以缺失情况基本分析一文中生成的缺失数据为例。调查了33名研究对象的性别(gender)、年龄(age)和某生化指标(X)，分析性别和年龄对生化指标浓度是否有影响？人为生成一个有缺失值(生化指标缺失10个个案，并且都是在高年龄组缺失)的数据(见图1)，然后再进行填补分析。本案例数据可在“附件下载”处下载。

二、回归算法填补

（一） 软件操作

选择“分析”—“缺失值分析”(图2)。

将“年龄”和“生化指标”选入“定量变量”，“性别”选入“分类变量”，勾选“EM”(图3)。

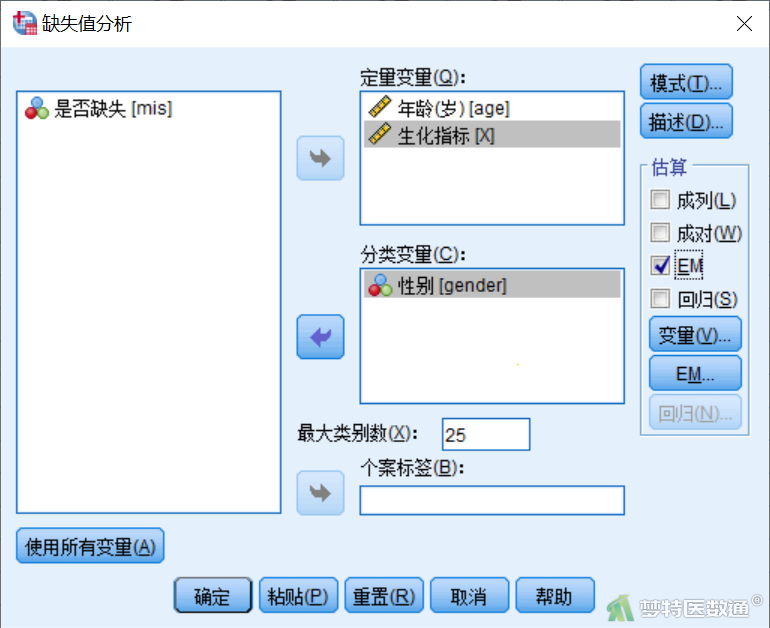
点击“变量”，进入“缺失值分析：EM的变量以及回归”对话框 ，选择“使用所有定量变量”。此处默认情况下为使用所有定量变量进行估计。如果不希望这样做，可以选择“选择变量”，将因变量(缺失变量)选入上方的“预测变量(D)”框，将自变量选入下方的“预测变量(R)”框。如果一个变量可以同时成为因变量和自变量，此时可以使用中间的“两者”按钮将其同时选入两个框(图4)。

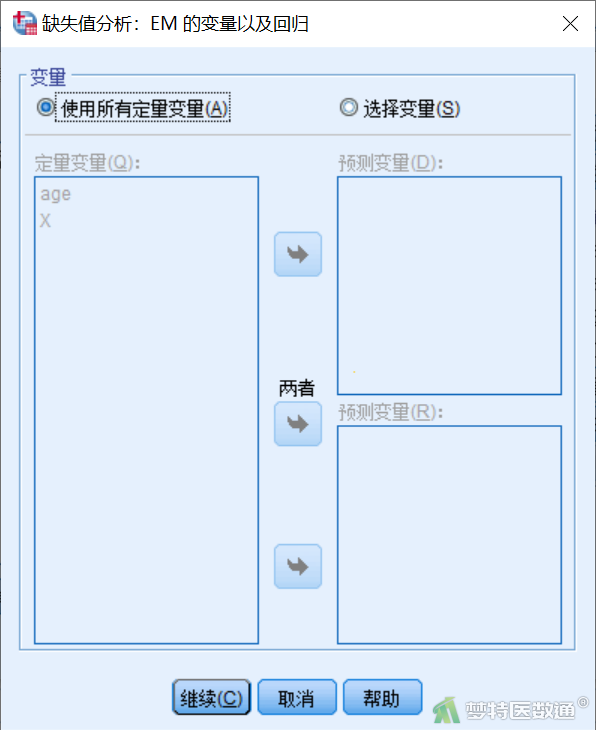
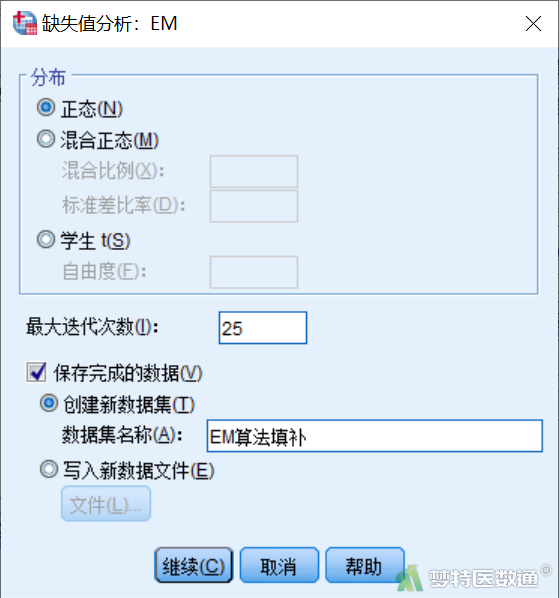
点击“EM”，进入“缺失值分析：EM”对话框，其中的“分布”框用于设置变量的分布形式，默认为正态分布。可以更改为混合正态分布或者t分布。后两种情况需要进一步设定相应的参数，如混合正态分布中的混合比例、标准差比以及t分布中的自由度(图5)。“保存完成的数据”复选框用于要求替换后的数据集生成新的数据集。

最后可生成一个新的数据集“EM算法填补”，可在“附件下载”处下载比较。

（二）效果比较

替补后可出现Little’s MCAR检验，结果为无效假设(P=0.018)，认为数据缺失不是完全随机缺失。

对数据集“EM算法填补”进行重新分析，然后与缺失值填补——回归算法填补法(链接)分析结果进行对比见表1。

表1

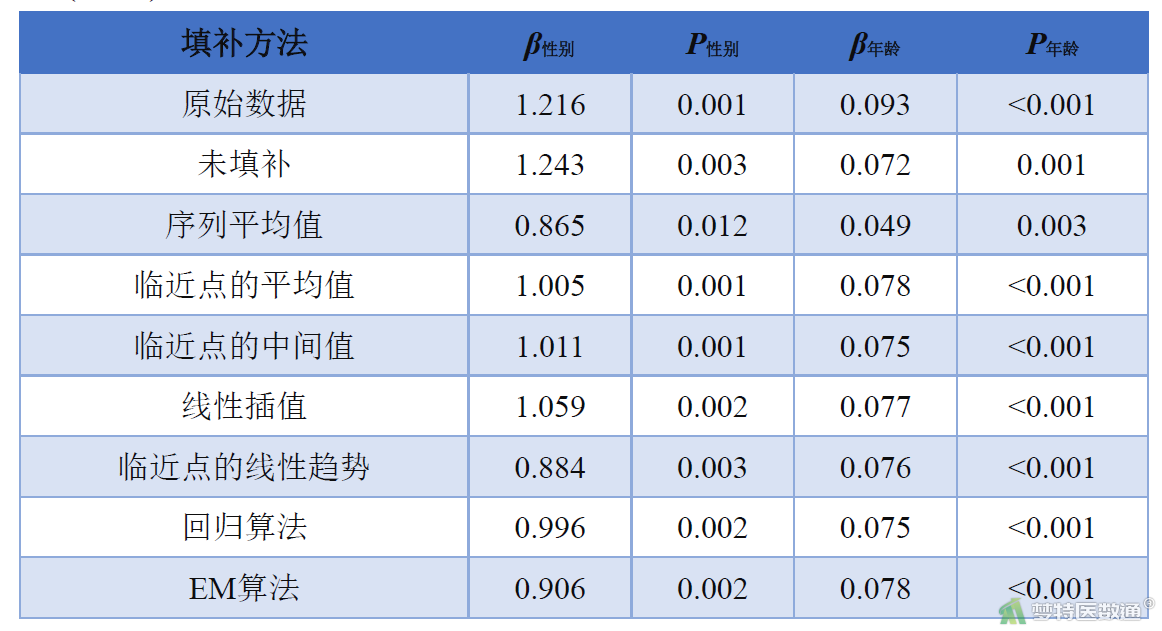
通过对比可知，EM算法只比“序列平均值”效果好，与其他几种方法相比并未体现出明显优势。