对数据缺失情况进行分析是后续进一步选择合适的数据处理措施的前提。本文将实例演示在SPSS软件中对缺失数据进行基本分析的步骤。
关键词:SPSS; 缺失数据; 缺失机制; 缺失值填补
一、案例数据
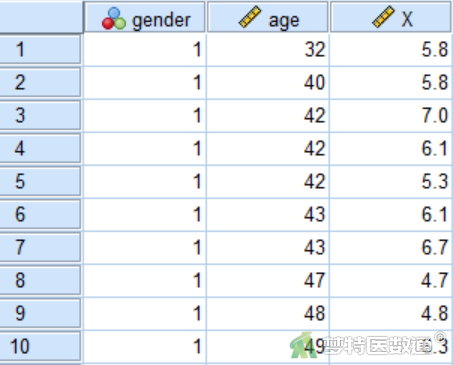
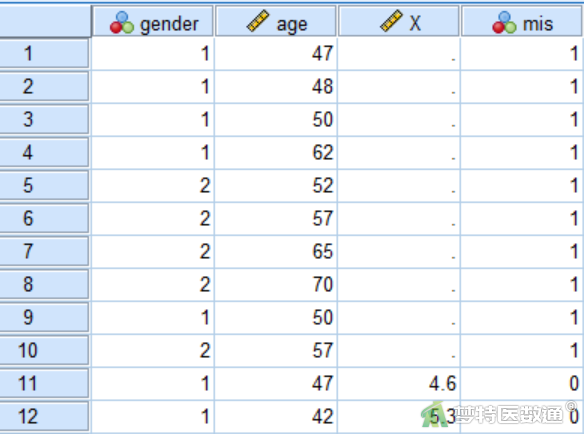
调查了33名研究对象的性别(gender)、年龄(age)和某生化指标(X),分析性别和年龄对生化指标浓度是否有影响?部分数据见图1,本案例数据可从“附件下载”处下载。
二、生成缺失数据
现对完整数据进行多重线性回归分析,操作详见多重线性回归分析(Multiple Linear Regression Analysis)——SPSS软件实现(链接),的到如图2结果:
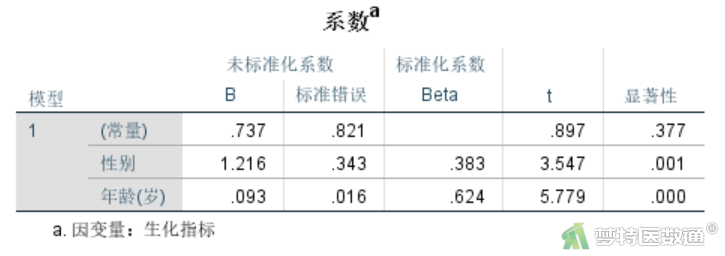
为了使分析结果有对照标准,这里人为生成一个有缺失值(生化指标缺失10个个案,并且都是在高年龄组缺失)的数据(图3),缺失数据集也可在“附件下载”处下载,然后再进行填补分析。
分析未经过任何填补方法处理的情况(此时对缺失值采取“成对排除个案”,图4),结果见图5。


可见未经填补处理的数据分析结果,年龄的回归系数与原始数据之间存在较大差异。
三、缺失模式分析
(一) 软件操作
选择“分析”—“缺失值分析”(图6)。
将“年龄”“生化指标”选入“定量变量”框;将“性别”选入“分类变量”框(图7)。
在“缺失值分析:模式”子对话框中选中所有的复选框(图8)。
(二) 结果解读
图9为单变量统计结果,该表格为每个变量显示非缺失值的样本量、平均值、标准差,同时会显示缺失值的计数和百分比。从中可见在三个变量中只有生化指标X有10个缺失值,缺失比例为30.3%。gender由于被指定为分类变量,因此不会输出平均值和标准差。
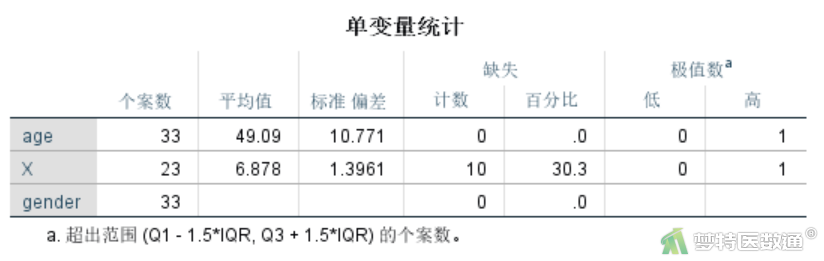
图10“数据模式(所有个案)”结果,给出了所有案例的缺失值,S表示缺失,+号表示极值。该表格的信息和图11“缺失模式(具有缺失值的个案)”完全相同。
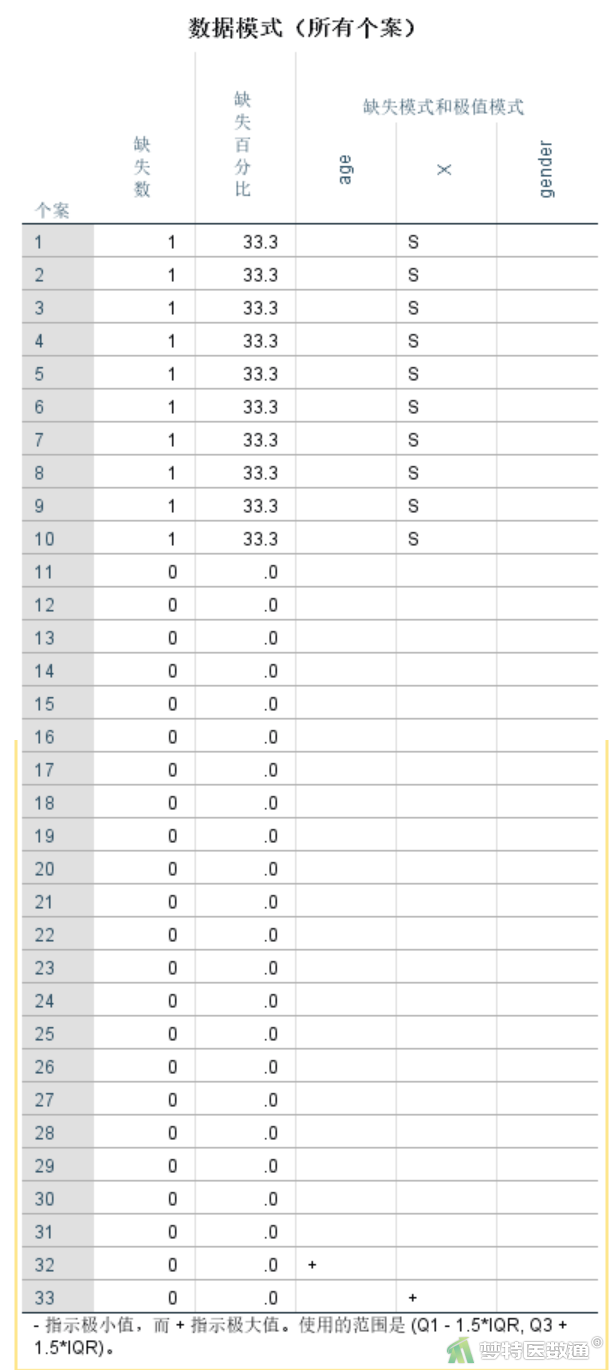
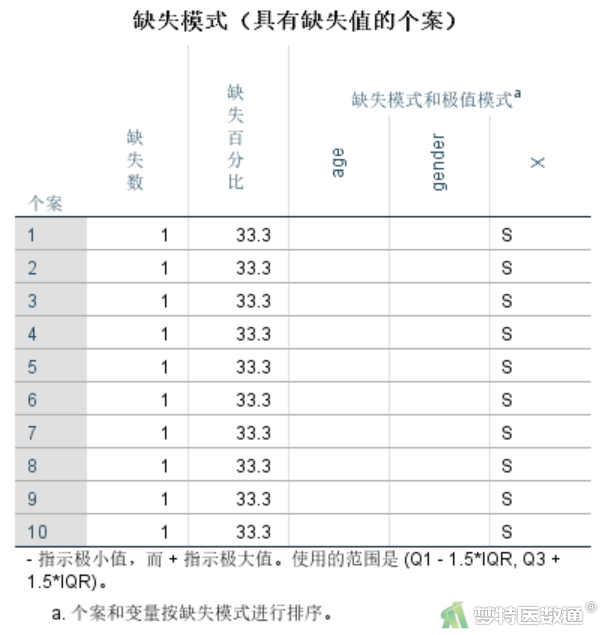
图12“制表模式”结果为全部进入缺失值分析的变量。可见33个案例中共有10个案例的生化指标X存在缺失值,其他两个变量则均无缺失情况出现。

四、数据缺失性质分析
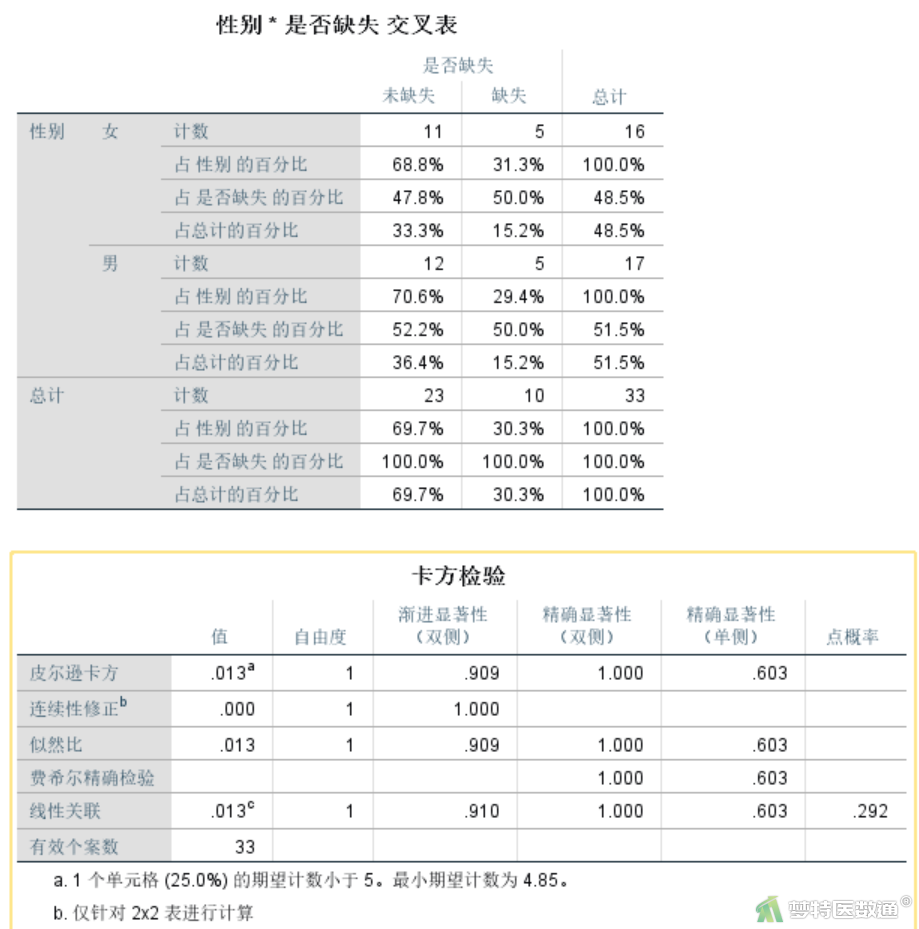
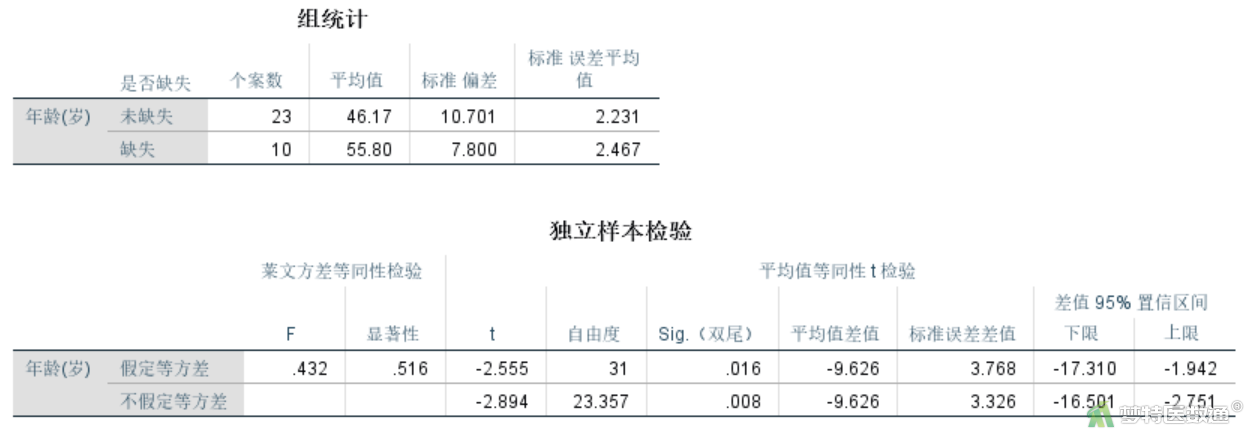
下面对上述案例的缺失类型进行分析,对缺失值与性别之间的关系使用fisher’s精确概率法(操作详见2×2 Fisher确切概率法(2×2 Fisher’s Exact Test)——SPSS软件实现,链接),对缺失值与年龄之间的关系使用两独立样本t检验(操作详见独立样本t检验(Independent Samples t-test)——SPSS软件实现,链接)。
性别的缺失情况(图13)分析显示,男、女性中缺失的比例分别为29.4%和31.3%,差异无统计学意义(P=0.603)。年龄的缺失情况(图14)分析显示,缺失组和非缺失组的年龄分别为(55.8±7.8)岁、(46.2±10.7)岁,差异有统计学意义(P=0.016)。说明缺失数据与年龄有关,并不是属于完全随机缺失,而可以认为是属于随机缺失。