在前面文章中介绍了(提高诊断试验效率:多变量综合诊断——SPSS软件实现),本文使用同样的案例介绍在Medcalc软件中实现多变量综合诊断的步骤。
关键词:Medcalc; 诊断试验; 多变量综合诊断; logistic回归
由于多个指标之间通常具有一定的互补作用,所以利用多个指标进行综合诊断能够在一定程度上提高诊断的准确度。在进行多指标联合诊断时,对于具有明确诊断阈值或定性诊断的情况,可以使用平行诊断和序贯诊断提高诊断试验效率;对于检测结果为定量或有序的情况,使用多变量诊断模型更为合适。临床医生可以选择合适的多变量模型(如logistic回归等)或机器学习方法(如支持向量机、随机森林等)构建诊断模型。
一、案例简述
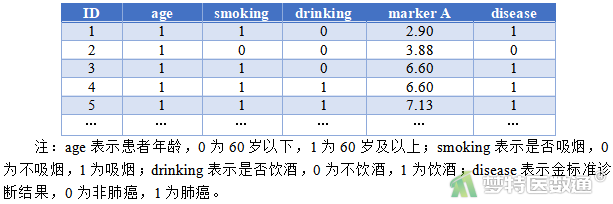
某课题组预通过就诊者的基本特征、实验室检查等多个指标判断其是否患有肺癌,并评价该综合诊断方法的准确度。研究共纳入424例就诊者,诊断指标包括就诊者的年龄、是否吸烟、是否饮酒、肿瘤标志物A;肺癌诊断的金标准为穿刺活检病理检查。部分数据见图1,本文案例可从“附件下载”处下载。
二、问题分析
本案例的分析目的是评价通过就诊者的基本特征、实验室检查等多个指标综合诊断是否患肺癌的准确性,可以金标准诊断结果为因变量,多个诊断指标为自变量构建logistic回归模型,然后根据该多变量诊断模型计算得到的预测值绘制多变量综合诊断的ROC曲线,通过ROC曲线下面积评价模型准确性。
三、软件操作及结果解读
(一) 单因素分析
1. 软件操作
- 打开Medcalc软件,导入数据如图2所示。
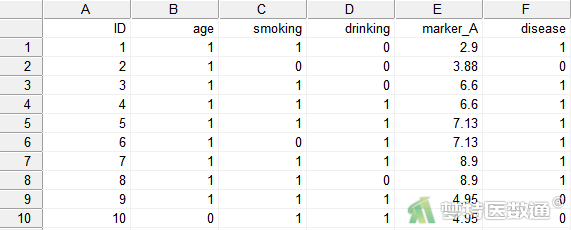
- 为相应变量名称和水平设置中文标签。如图3所示。
- 点击“统计”-“回归”-“逻辑回归”(图4)。
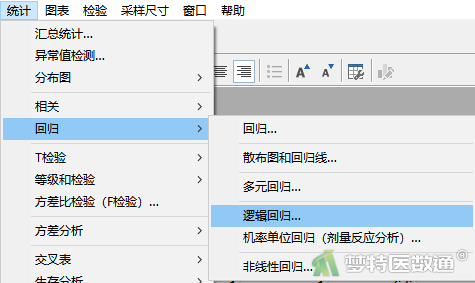
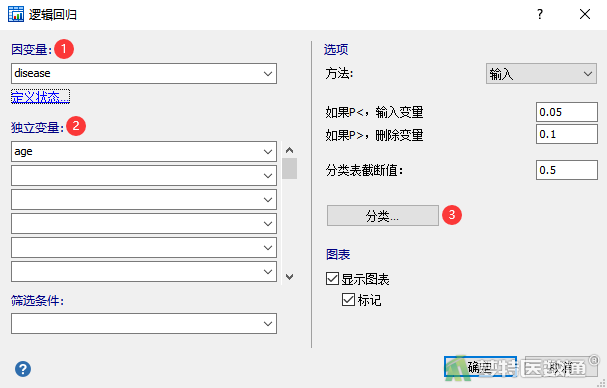
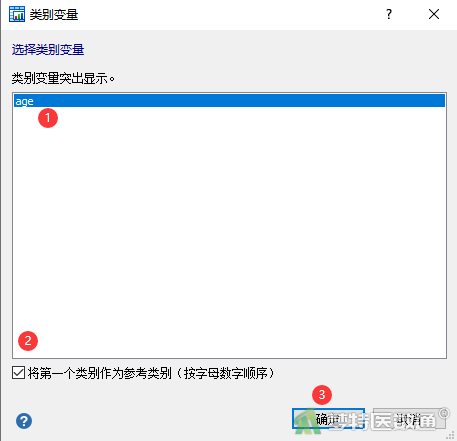
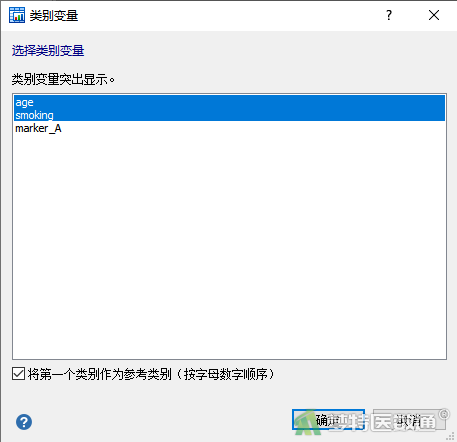
- 在“逻辑回归”对话框中,“因变量”下选择金标准诊断结果“disease”,“独立变量”处选择进行单因素分析的变量“age”。注意虽然在“独立变量”处设置了多个选择框,但单因素分析时每次只能选择一个变量,如果同时选择多个独立变量,就是多因素分析。因为“age”为分类变量,所以点击右侧“分类”按钮(图5),在“类别变量”对话框中选中分类变量“age”,如果要将分类变量的参照类别改为以第一类为参照,则勾选下方的“将第一个类别作为参考类别”(图6),然后点击确定回到“逻辑回归”对话框,最后点击“确定”。
- 按照以上“逻辑回归”对话框中的操作步骤,分别将其他要进行单因素分析的变量“smoking”、“drinking”“marker_A”依次选入“独立变量”中。此处还要注意的是,当独立变量中是分类变量时(“smoking”、“drinking”)需要点击“分类”进行哑变量设置,是连续变量时(“marker_A”)则不需要设置。
2. 结果解读
完成以上步骤后可以得到单因素分析结果,单因素分析时,可以将检验水准提高到0.1。
图7显示了“age”的单因素分析结果,P<0.001,有统计学意义,故考虑在多因素分析时纳入该变量。下方还给出了OR值及其95%CI,在单因素分析中不必过多关注。
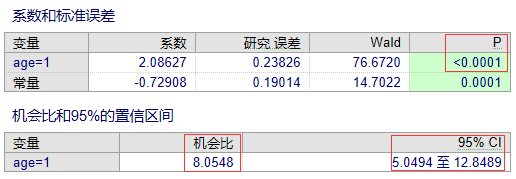
图8显示了“drinking”的检验结果,P=0.1156,没有统计学意义,故考虑在多因素分析时不纳入该变量。

图9显示了“smoking”的检验结果,P<0.001,有统计学意义,故考虑在多因素分析时纳入该变量。

图10显示了“marker_A”的检验结果,P<0.001,有统计学意义,故考虑在多因素分析时纳入该变量。

综合以上单因素分析结果,得出变量“age”、“smoking”和“marker_A”可以纳入多因素分析模型。
(二) 多变量综合诊断
1. 软件操作
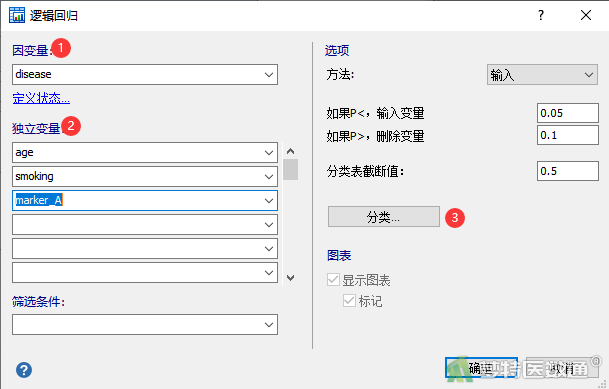
- 多因素分析也在“逻辑回归”对话框中进行,和单因素分析不同的是,多因素分析时可以在“独立变量”中同时选择多个进行多因素分析的变量,此处选择变量“age”、“smoking”和“marker_A”,因为存在分类变量,所以点击右侧“分类”按钮(图11),在“类别变量”对话框中选中分类变量“age”和“smoking”,勾选下方的“将第一个类别作为参考类别”,然后点击确定回到“逻辑回归”对话框,最后点击“确定”(图12)。
2. 结果解读
图13是多因素分析结果,显示年龄“age”、是否吸烟“smoking”和肿瘤标志物A“marker_A”都与“是否发生肺癌”有统计学关联(P<0.05),高年龄组的肺癌发生风险是低年龄组的5.036 (95%CI:2.944~8.613)倍,吸烟者的肺癌发生风险是不吸烟者的6.925 (95%CI:4.126~11.622)倍,肿瘤标志物A每增加一个单位,肺癌发生风险增加1.521 (95%CI:1.303~1.777)倍。据此,可得到每个就诊者根据“年龄”、“是否吸烟”和“肿瘤标志物A”三个因素,诊断“是否患肺癌”的危险得分Logit(P):
Logit(P) = -4.068 + 1.617×年龄 + 1.935×是否吸烟(不吸烟=0,吸烟=1)+ 0.420×肿瘤标志物A
然后在模型实际应用中可以按照以下公式,计算得到每一个就诊者诊断为肺癌的预测概率:
\(P=\frac{e^{\operatorname{Logit}(P)}}{1+e^{\operatorname{Logit}(P)}}\)
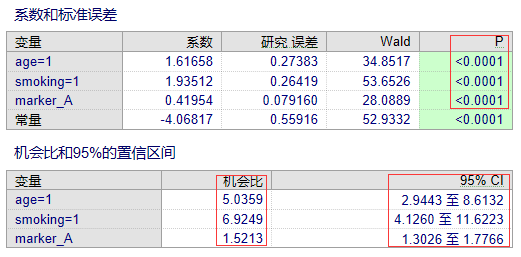
图14是多因素分析结果中的ROC曲线分析结果,得到该多因素模型的ROC曲线下面积(AUC)及其95%CI为0.859 (95%CI:0.823~0.891),此时就完成了多变量综合诊断模型的构建及其AUC的计算。

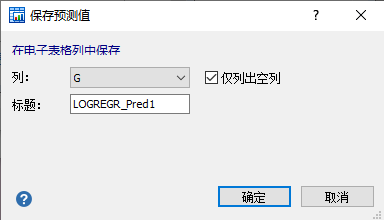
如果需要进一步绘制多变量诊断模型的ROC曲线及对单因素和多因素诊断模型进行比较,则需要先生成多因素回归模型预测的患病概率。点击多因素分析结果最下方的“保存预测概率”(图14),出现“保存预测值”对话框,在此处可以设置新变量在表格中的保存位置及名称(图15),点击“确定”后就可以在数据表中看到新变量“LOGREGR_Pred1”(图16)。

(三) ROC曲线比较
1. 软件操作
- 点击“统计”-“ROC曲线”-“ROC曲线对比”(图17)。
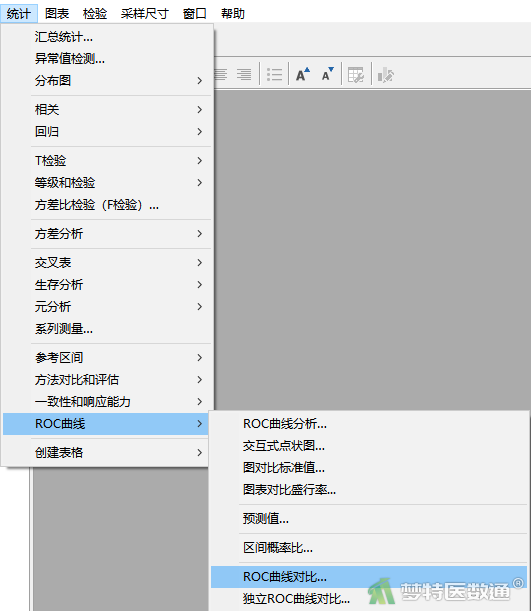
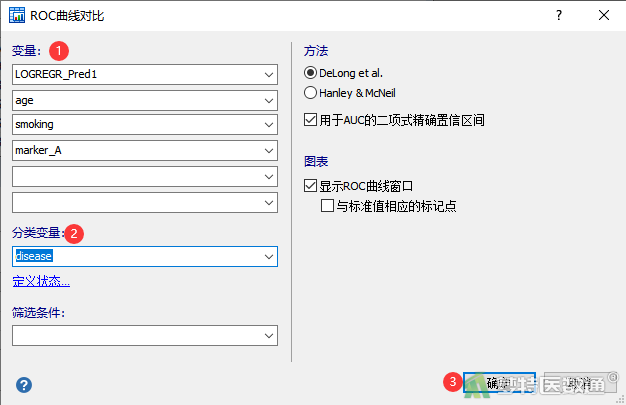
- 在“ROC曲线对比”对话框中,“变量”下选择“LOGREGR_Pred1”、“age”、“smoking”和“marker_A”,“分类变量”下选择金标准诊断结果“disease”最后点击“确定”(图18)。
2. 结果解读
图19是单变量诊断和多变量综合诊断的ROC曲线,从图中可以大致看出综合诊断的曲线下面积明显大于单变量诊断(图19)。

图20显示了多个单变量诊断和多变量综合诊断对应的ROC曲线下面积(AUC)及其95%CI。其中综合诊断曲线下面积为0.859 (95%CI:0.823~0.896),和上述多因素Logistic回归分析中得到的AUC值一致。其他三个单变量诊断的AUC均不足0.8(图20)。
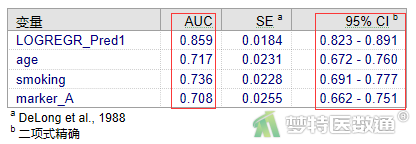
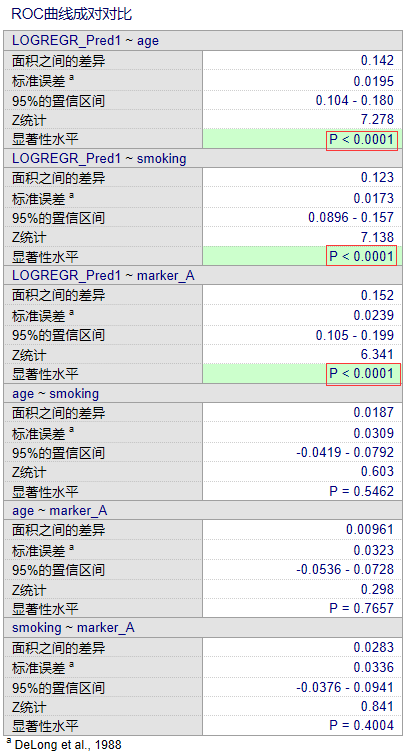
图21是对上述四个诊断模型进行两两比较的结果,重点观察综合诊断模型和单变量诊断模型的AUC是否有差异。结果显示,综合诊断分别和三个单变量诊断模型的AUC进行比较时,两者之间的差异均有统计学意义(P<0.001),综合诊断模型的准确度大于三个单变量诊断模型。SPSS不能在ROC分析模块中直接给出各诊断模型ROC曲线下面积比较的P值(提高诊断试验效率:多变量综合诊断——SPSS软件实现)。
四、结论
本案例通过单因素分析,筛选出年龄、是否吸烟和肿瘤标志物A与“是否发生肺癌”可能存在统计学关联(P<0.1),将这三个变量纳入多因素Logistic模型进行分析,得到这三个变量都与“是否发生肺癌”有统计学关联(P<0.05),高年龄组的肺癌发生风险是低年龄组的5.036 (95%CI:2.944~8.613)倍,吸烟者的肺癌发生风险是不吸烟者的6.925 (95%CI:4.126~11.622)倍,肿瘤标志物A每增加一个单位,肺癌发生风险增加52.1% (OR=1.521,95%CI:1.303~1.777)倍。多因素模型的ROC分析曲线下面积(AUC)及其95%CI为0.859 (95%CI:0.823~0.891)。通过生成预测概率,同时绘制了单因素和多因素诊断模型的ROC曲线并进行了ROC曲线分析,结果显示多变量诊断模型AUC显著高于单变量模型(P<0.001),可以认为该多变量诊断试验准确性显著高于其他三个单变量诊断模型。
五、知识小贴士
(一) 预测模型
多变量预测模型分为两大类:诊断模型和预后模型。两者的主要区别是时间的概念。诊断模型是多个预测因素(通常为诊断测试结果)被组合在一起来估计预测时,是否存在某种疾病或状况的概率,通常是横断面的。而预后模型是多个预测因素被结合起来估计未来某个时期发生特定事件(如死亡、疾病复发、出现并发症等)的概率,通常是纵向的。个体预后或诊断的多变量预测模型的透明报告 (TRIPOD)是为了改进不论以诊断或预后为目的而开发、验证或更新预测模型的研究报告。质量较高的多变量预测模型都会遵循TRIPOD的指导研究。
(二) 变量筛选
本案例分析结果显示利用多变量进行ROC诊断的效率优于单变量,其实这是建模中普遍存在的真理,即随着纳入变量的增多,诊断模型的准确性总会变得越高。但在多变量模型构建时并不是纳入变量越多越好,因为要从专业角度综合考虑,纳入有专业意义且影响较大的变量,要避免出现过度拟合从而影响模型外推。同时从模型的实用性角度考虑,因为预测概率需要通过模型计算得出,而非可观测的指标,纳入变量越多,模型越复杂,计算难度越大,不利于模型推广。
(三) 模型验证
评价多变量诊断模型的诊断准确度,可以采用内部数据验证的方法,即通过建立预测模型,比较不同组之间预测值分布之间的差别,或者使用交叉验证(LOO-CV)的方法,但更可信的方法是使用前瞻性研究数据验证诊断准确度。为了避免模型的过度拟合,有些模型必须要进行外部数据验证,III期诊断试验的评价需要使用外部数据进行验证。
(四) 模型应用
上述模型需要通过将就诊者各参数信息代入公式后计算得到Logit(P),再通过与模型截断值比较,做出是否患病的判断。