医学研究之生存分析的样本量计算——指数模型的两风险率差的非劣效性检验

关键词：样本量计算; PASS; 生存分析;两风险率差的非劣效性检验

一、案例数据

某研究者计划开展一项两组1：1平行对照设计的临床研究，以研究新疗法治疗某癌症的效果是否不比传统疗法差。已知传统疗法治疗某癌症的风险率为0.6。计划让受试者进组的时间为1年，且期望全部受试者能够均匀地进入研究。随访时间为2年，预计两组的失访率均为0.05，风险率差为0。若非劣效性差值为0.2，取α=0.05，β=0.1，试估计所需的样本含量？

二、案例分析

本研究中已知对照组的风险率，欲研究新疗法组治疗某癌症的风险是否非劣效于传统治疗组，假设生存时间遵循指数分布，可采用两风险率差的非劣效性检验，其样本量计算需要以下几个参数：

• 受试者入组时间(年)，本例中为1
• 研究者入组模式，本例为期望全部受试者能够均匀地进入研究
• 随访时间(年)，本例为2
• 对照组的风险率，本例为0.6
• 处理组和对照组的风险率差，本例为0
• 非劣效性差值，本例为0.2
• 两组失访率，本例均为0.05
• 检验水准α (通常取0.01至0.1)，本例取0.05
• 检验功效1-β (通常为0.8或更高)，本例取0.9

三、软件操作

(一) 方法选择

在左侧界面中依次选择“Procedures (程序)”—“Survival (生存分析)”—“Two Survival Curves (两样本生存曲线)”—“Non-Inferiority(非劣效性检验)”—“Non-Inferiority Tests for the Difference of Two Hazard Rates Assuming an Exponential Model (假设指数模型的两风险率差的非劣效性检验)”。

(二) 参数设置

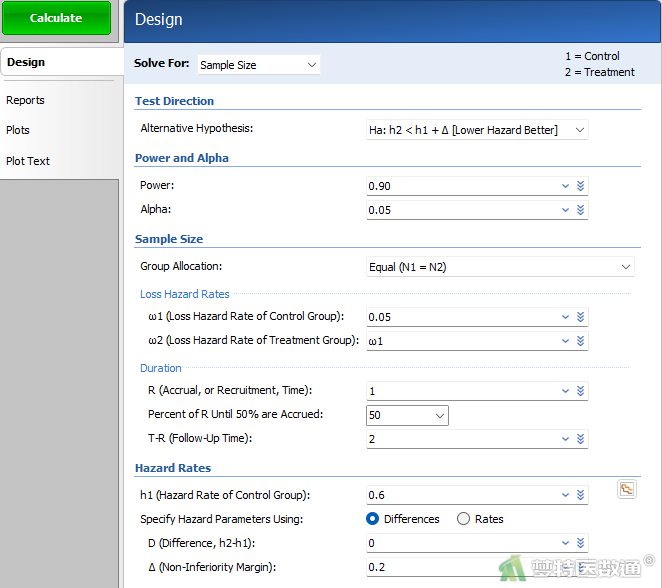
在“Design (设置)”模块中按以下参数设置相应选项(图2)：

• Solve For：选择“Sample Size”，表示本分析的目的是用于计算样本量。
• Alternative Hypothesis：指定备择假设的方向。选择“H_a ： h₂< h₁ + Δ [Lower Hazard Better]”，表示较低的风险率更优。
• Power and Alpha：Power为把握度，填0.90；Alpha为检验水准，填0.05。
• Group Allocation：选择“Equal (N1=N2)”，表示每组的样本量相等。
• Loss Hazard Rate：ω₁(Loss Hazard Rate of Control Group)：表示对照组失访风险率，可为任意非负数。本例均填0.05；ω₂(Loss Hazard Rate of Treatment Group)：表示处理组失访风险率，已知两组失访率相等，本例填“ω₁”。
• R (Accrual, or Recruitment, Time)：即入组时间，表示受试者进入研究的时间长度。本例填1。
• Percent of R Until 50% are Accrued：即招募50%的受试者的累积时间百分比，以控制受试者的入组模式。若期望受试者均匀入组，则设置为50；若期望更多的受试者早期入组，则设置为小于50的值；若期望更多的受试者后期入组，则设置为大于50的值。本例中填50。
• T-R (Follow-Up Time)：即随访时间，指最后一个受试者入组到研究结束之间的时间长度。本例填2。
• h₁ (Hazard Rate of Control Group)：即对照组的风险率(瞬时失效率)。在此过程中使用的指数生存分布假设风险率在整个实验中是恒定的，且风险率等于每单位时间平均事件数目的倒数。本例填0.6。
• Specify Hazard Parameters Using： 指定计算处理组风险率的参数。包括【Differences】和【Rate】，本例选择“Diifferences”。

D (Difference, h₂-h₁)：表示处理组和对照组的风险率差，本例填0。

Δ (Non-Inferiority Margin)：即非劣效性差值，表示仍可得出处理组非劣效于 对照组的h₂低于(或高于) h₁的最小距离。本例填0.2。

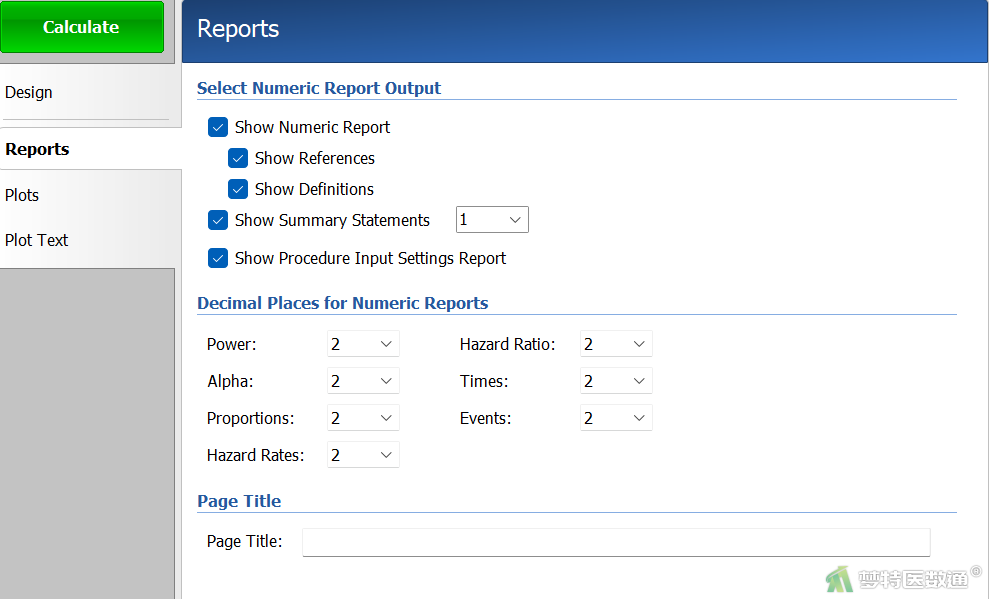
(三) 报告设置

在“Reports (结果报告)”模块中按图3设置输出结果格式，然后点击“Calculate (计算)”。

四、结果及解释

图4列出了该研究设计的相关参数和样本量计算结果，可知计算的每组样本例数(N)为209，总例数为418。

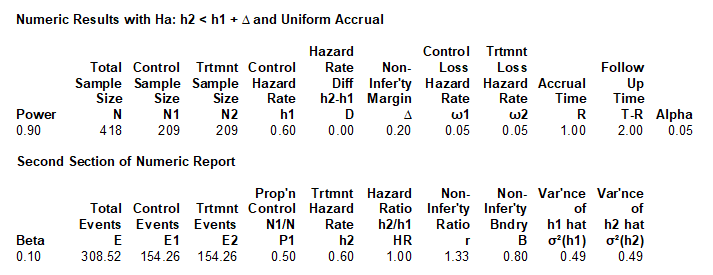
图5“References (参考文献)”列出了该计算过程中参考的相关文献；“Report Definitions (报告定义)”列出了各个参数的具体解释；“Summary Statements (报告概述)”为整个分析报告的摘要。

图6为此次样本量估算整个过程的详细参数设置汇总。

五、结论

该案例为指数模型的两风险率差的非劣效性检验的样本量计算。欲比较新疗法(处理组)治疗某癌症的风险不比传统疗法(对照组)差，采用1：1平行组设计。已知两组样本量相等，且均匀地在1年内进入研究，共随访2年，预计在结束时两组受试者失访率均为0.05。已知非劣效性差值为0.2，对照组治疗的风险率为0.6，两组风险率差为0，若取检验水准α取0.05、把握度β取0.90。则每组至少需要209例患者参与研究，共至少需要418例研究对象。