医学研究之回归分析的样本量计算——多重线性回归分析的决定系数法

关键词：样本量计算; PASS; 回归分析; 直线回归; 多重线性回归分析的样本量计算

一、案例数据

某研究者欲进行糖尿病患者人群血糖的影响因素研究，主要纳入胰岛素、血压、血脂、生长素等影响因素。研究者期望有足够的样本含量来检验决定系数R²至少为0.2，而R²实际值为0.5。取α =0.05，β=0.1，试估计所需的样本含量。

二、案例分析

本研究欲调查一个因变量与多个自变量的关系，采用多重线性回归分析，已知回归分析的决定系数值，可使用决定系数法估计样本量。多重线性回归分析决定系数样本量计算需要以下几个参数：

1. 控制变量数，本例中为0。

2. 显著性检验的自变量数，本例为4。

3. 原假设H₀下复相关系数的平方，本例为0.2。

4. 备择假设H₁下复相关系数的平方，本例为0.5。

5. 检验水准α (通常取0.01至0.1，本研究取0.05)。

6. 检验功效1-β (通常为0.8或更高，本研究取0.9)。

7. 脱失率DR (通常不宜超过20%，本研究取10%)。

三、软件操作

(一) 方法选择

在左侧界面中依次选择“Procedures (程序)”—“Regression (回归)”—“Multiple Regression (多重回归)”—“Multiple Regression (多重回归)”，见图1。

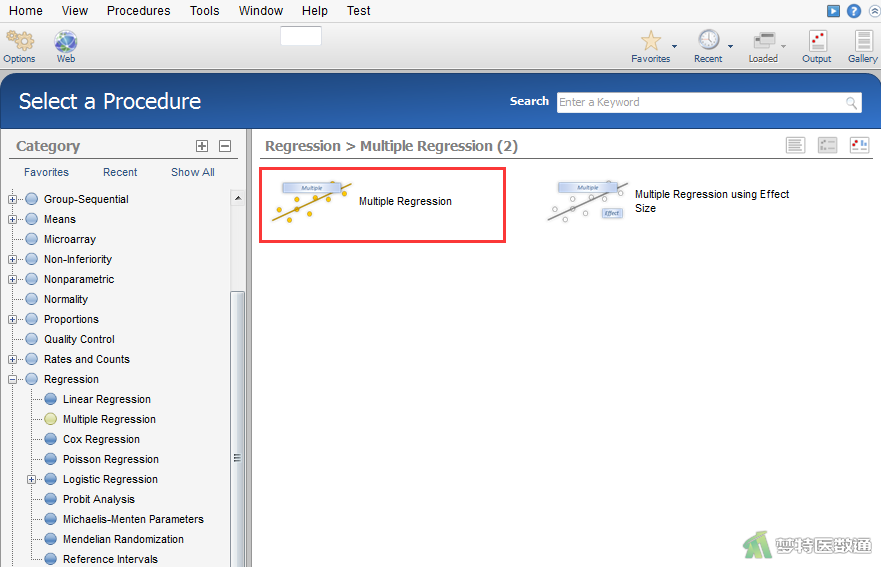
(二) 参数设置

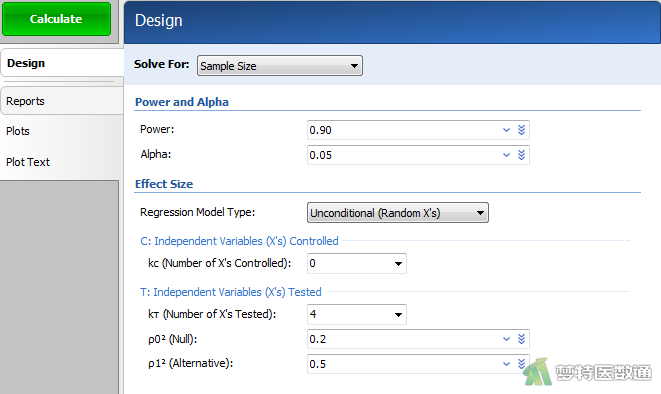
在“Design (设置)”模块中按以下参数设置相应选项(图2)：

①Solve For：选择“Sample Size”，表示本分析的目的是用于计算样本量。

②Power and Alpha：Power为把握度，填写“0.90”；Alpha为检验水准，填写“0.05”。

③Regression Model Type：表示多重回归数据的建立和分析的两种方法，包括【Unconditional (Random X's)】无条件法和【Conditional (Fixed X's)】条件法。无条件法假设Y和X服从多元正态分布，因此在研究过程中直到观察到X值才能知道X的值，是最实际的方法。条件法假设X值在计划阶段已知，而这种情况在现实中很少发生，所以这种方法通常是不合理的。本例选择无条件法。

④kc (Number of X’s Controlled)：即控制变量数，kc ≥ 0且kc + k_T < N-1。本例填“0”。

⑤k_T (Number of Independent Variables Tested)：即进行显著性检验的自变量数，k_T ≥1且kc + k_T < N-1。本例填“4”。

⑥ρ₀² (Null)：即原假设H₀下复相关系数的平方，仅在无条件模型中显示。ρ₀²是R²的总体值，如果指定了控制变量X，该值即为偏相关系数的平方。范围介于0~1。Cohen将该值解释为0.02 =小，0.13 =中，0.26 =大。本例填“0.2”。

⑦ρ₁² (Alternative)：即备择假设H₁下复相关系数的平方，仅在无条件模型中显示。Ρ₁²是R²的总体值，如果指定了控制变量X，该值即为偏相关系数的平方。范围介于0~1。Cohen将该值解释为0.02 =小，0.13 =中，0.26 =大。本例填“0.5”。

(三) 脱失率设置

在“Reports (结果报告)”模块中，勾选“Show Dropout-Inflated Sample Size Report (报告脱失样本量)”，在“Dropout Rate”中填写“10%”(图3)，表示按照10%的脱失率计算样本量。设置好上述参数后点击“Calculate (计算)”。

四、结果及解释

图4列出了该研究设计的相关参数和样本量计算结果，可知计算的样本例数(N)为60。

图5“References (参考文献)”列出了该计算过程中参考的相关文献；“Report Definitions (报告定义)”列出了各个参数的具体解释；“Summary Statements (报告概述)”为整个分析报告的摘要。

图6“Dropout-Inflated Sample Size (脱失样本量)”为考虑了脱失率的样本量(N')，也是研究实际开展过程中需要达到的最低样本量，本研究中为67。

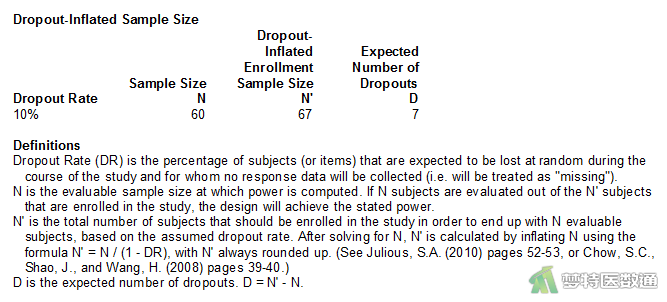
图7为此次样本量估算整个过程的详细参数设置汇总。

五、结论

本研究中血糖、胰岛素、血压、血脂和生长素均为连续性变量，欲研究血糖与其他4个变量之间的关系，可采用多重线性回归分析。已知实际决定系数为0.5，期望决定系数不小于0.2，若取检验水准0.05，检验功效0.90，至少需要60例研究对象。若考虑10%的脱失率，则至少需要67例研究对象。