在前面文章中介绍了泊松回归分析(Poisson Regression Analysis)的假设检验理论,本文将实例演示在SPSS软件中实现泊松回归分析的操作步骤。
关键词:SPSS; 泊松回归; Poisson回归; 等离散
一、案例介绍
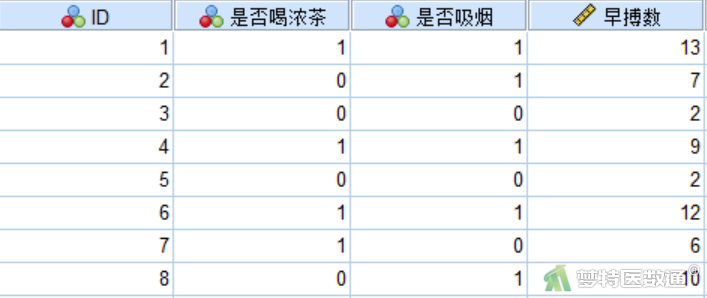
某临床医师对39名有胸闷症状的非器质性心脏病男性患者的24小时早搏数进行了临床研究记录,每个患者的研究因素包括是否喝浓茶、是否吸烟。请利用该资料对24小时早搏数的影响因素进行分析。
创建代表患者编号的变量“ID”;代表患者喝浓茶情况的分类变量“是否喝浓茶”,赋值为“0”和“1”(0为不喝浓茶1为喝浓茶);代表患者吸烟情况的分类变量“是否吸烟”,赋值为“0”和“1”(0为不吸烟,1为吸烟),以上变量测量尺度均设为“Nominal(名义)”;创建代表患者24小时早搏数的计数变量“早搏数”,测量尺度设为“Scale(标度)”。部分数据见图1。本文案例可从“附件下载”处下载。
二、问题分析
本案例的分析目的是了解有胸闷症状的非器质性心脏病男性患者24小时早搏数的影响因素。了解单位时间、单位面积或单位空间内某事件发生数的影响因素,可以考虑使用Poisson回归分析。但需要满足以下6个条件:
本案例的分析目的是了解有胸闷症状的非器质性心脏病男性患者24小时早搏数的影响因素。了解单位时间、单位面积或单位空间内某事件发生数的影响因素,可以考虑使用Poisson回归分析。但需要满足以下6个条件:
条件1:观察变量为计数变量。本研究中心脏病男性患者的24小时早搏数为计数变量,该条件满足。
条件2:观测值的发生相互独立。本研究中各研究对象的每次早搏事件发生都是独立的,不存在互相干扰的情况,该条件满足。
条件3:至少有1个自变量,可以是分类变量,也可以是连续变量。本研究中有两个分类自变量,分别为是否喝浓茶和是否吸烟,该条件满足。
条件 4:观察变量不存在显著的异常值,该条件需要通过软件分析后判断。
条件5:观察变量服从Poisson分布,即满足等离散性,表现为计数值的平均值(近似)等于方差。该条件可以通过数据特征进行初步判断,本研究的观察变量为心脏病男性患者24小时早搏数(计数资料),从专业知识可知,早搏发生频数较低,各单位时间内的发生情况相互独立,基本满足Poisson分布的条件。同时还也可以结合软件分析进行判断。
条件6:自变量之间无多重共线性。该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 适用条件判断
1. 条件4判断(异常值检测)
(1) 软件操作
① 点击“分析”—“描述统计”—“探索”(图2)。
② 在“探索”对话框中将变量“早搏数”选入“因变量列表”,点击“确定”(图3)。
(2) 结果解读
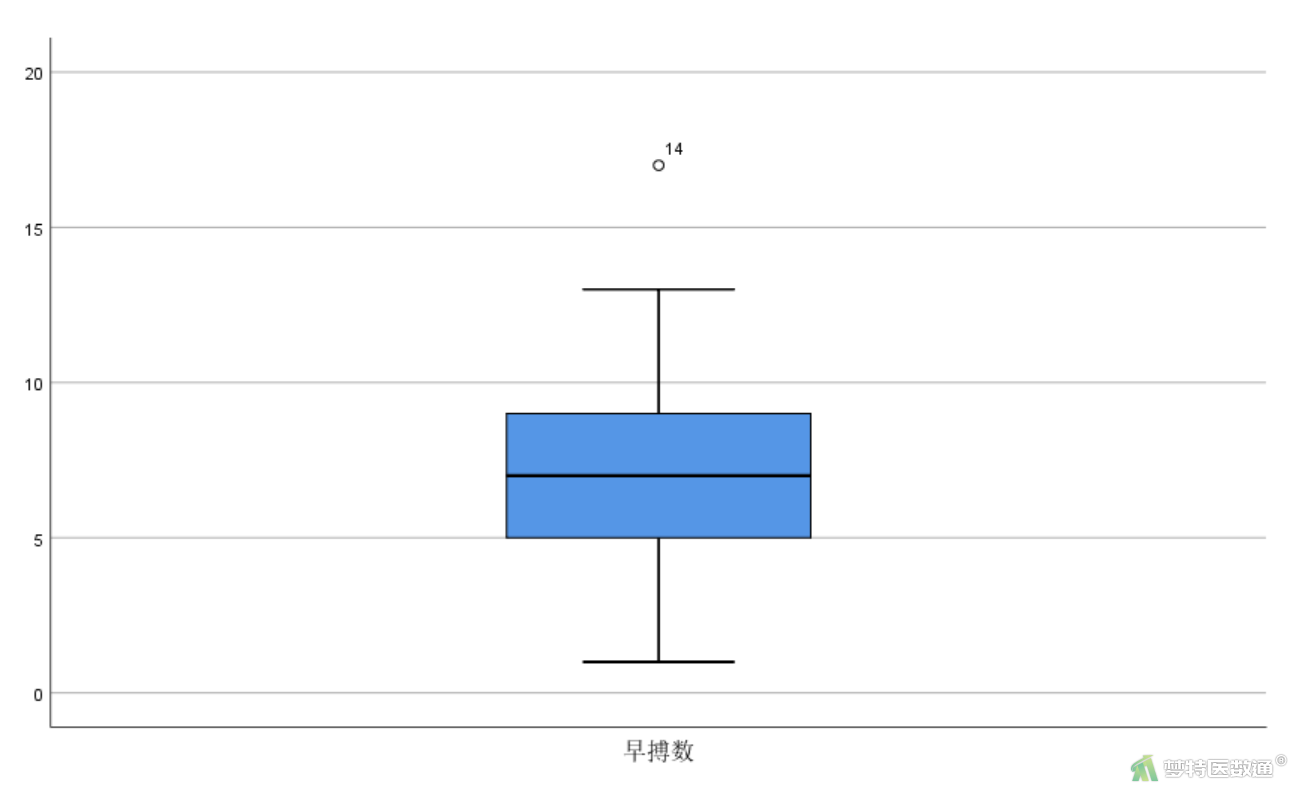
异常值通过箱线图和专业知识进行判断,图4箱线图提示存在一个异常值。查看数据表可以发现在早搏数的第14位数值为17,依据专业可判定该值可以保留。综上,本案例未发现需要处理的异常值,满足条件4。
2. 条件5判断(Poisson分布检验)
(1) 软件操作
① 点击“分析”—“非参数检验”—“旧对话框”—“单样本K-S检验”(图5)。

② 在“单样本K-S检验”对话框中将变量“早搏数”选入“检验变量列表”。下方“检验分布”中已默认勾选了“正态”进行正态性检验,本案例中需要进行Poisson分布检验,所以勾选“泊松”,然后点击“确定”(图6)。
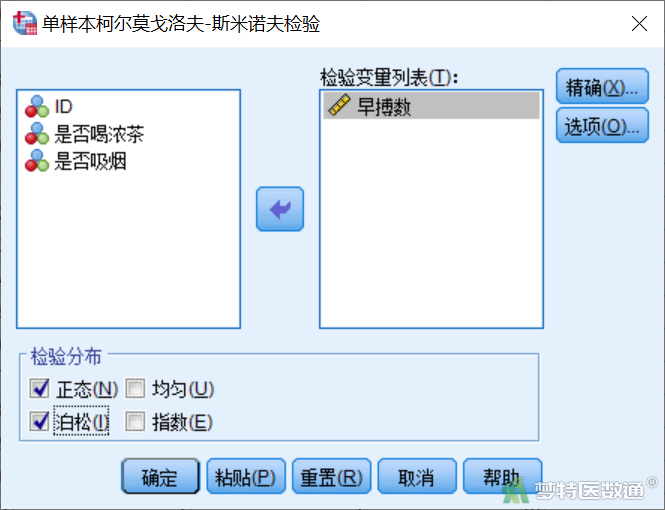
(2) 结果解读
结果分别输出了正态性检验和Poisson分布检验的结果。图7为Poisson分布检验结果,可以发现P=1.000>0.1,服从Poisson分布,满足条件5。此外,通过描述性分析也可发现早搏数的均数为7.31,方差为10.692,均数近似等于方差,也提示数据满足等离散性。
3. 条件6判断(多重共线性诊断)
(1) 软件操作
① 点击“分析”—“回归”—“线性”(图8)。
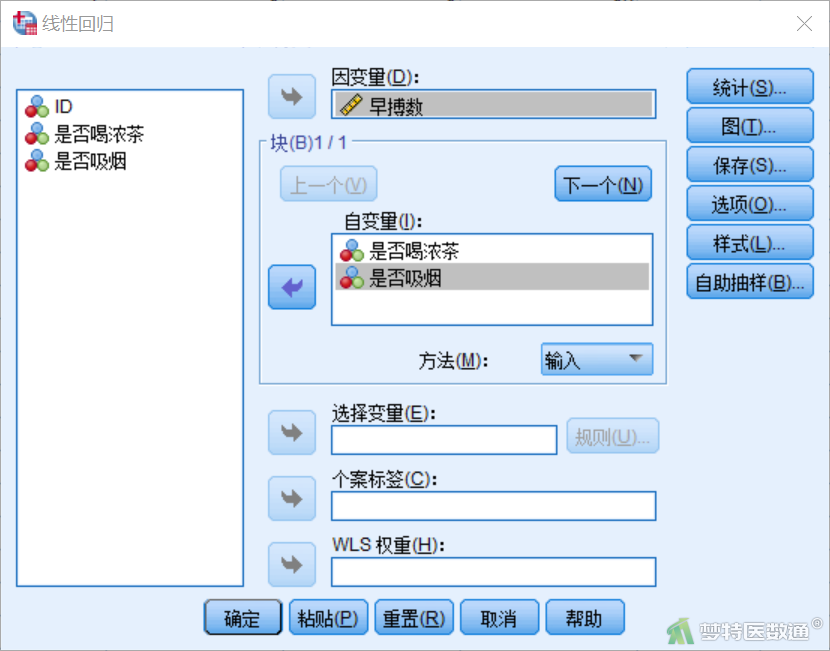
② 将变量“早搏数”选入“因变量”,变量“是否喝浓茶”和“是否吸烟”选入“自变量”(图9)。
③ 点击“统计”,在“统计”页面中勾选“共线性诊断”(图10),其他保持默认不变,点击“继续”后回到主对话框,点击“确定”。

(2) 结果解读
如果“容差”小于0.1或“VIF(方差膨胀因子)”大于10,则表示存在严重共线性。本例中,图11结果显示容忍度均为1,远大于0.1,方差膨胀因子均为1,远小于10,表明不存在严重多重共线性。

(二) 统计描述及推断
1. 软件操作
① 选择“分析”—“广义线性模型”—“广义线性模型...”(图12)。
② 在“广义线性模型”对话框中选择“模型类型”,在该页面下的“计数”部分选择“泊松对数线性”(图13)。

③ 在“广义线性模型”对话框中选择“响应”,在该页面下将变量“早搏数”选入右侧“因变量”框中(图14)。
④ 在“广义线性模型”对话框中选择“预测变量”,在该页面下将分类变量“是否喝浓茶”和“是否吸烟”选入右侧“因子”框中(图15)。点击下方的“选项”,在“选项”页面的“因子类别顺序”下选择“降序”,这样在构建模型时就是以“不喝浓茶”和“不吸烟”作为参照。然后点击“继续”回到主对话框。

⑤ 在“广义线性模型”对话框中选择“模型”,把页面中间的构建项类型选为“主效应”,然后将左侧变量“是否喝浓茶”和“是否吸烟”选入右侧“模型”框中(图17)。

⑥ 在“广义线性模型”对话框中选择“估算”,在该页面下的“协方差矩阵”部分选中“稳健估算量”,其他保持默认不变,如图18所示。
⑦ 在“广义线性模型”对话框中选择“统计”,在该页面下的“打印”部分选中“参数估计”下的“包括指数参数估计”,其他保持默认不变,如图19所示,然后点击“确定”。
2. 结果解读
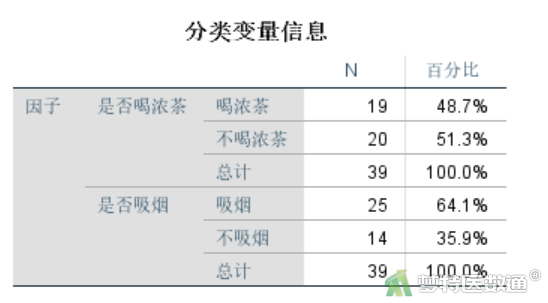
(1) 变量信息
图20和图21分别是对模型中的分类变量和连续变量的统计描述结果。

(2) 拟合优度检验
图22为拟合优度检验结果,AIC和BIC值用于多次分析时的对比,图中注释提示信息准则是越小越好,这两个值对于单独一个模型的信息准则意义不大。如果多次进行模型分析,可对比两个值的变化情况,综合说明模型构建的优化过程。
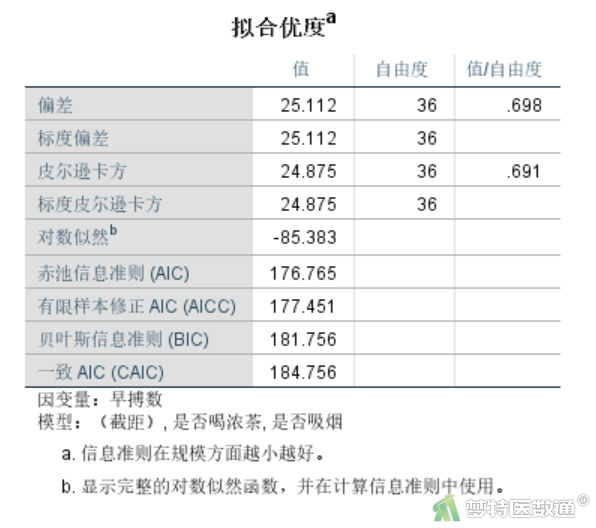
图23是Omnibus检验结果,可见似然比χ2值为32.884,P<0.001,表明所给资料拟合相应的Poisson回归模型是合适的,模型有统计学意义,模型中至少有一个自变量有统计学意义。

(3) 参数估计
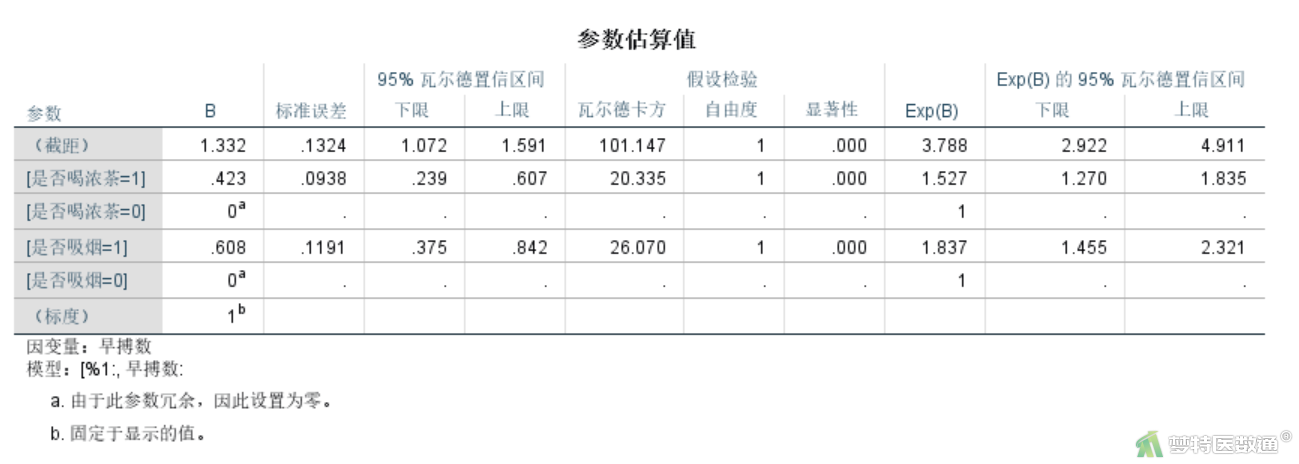
图24是模型效果检验结果,其中截距和变量“是否喝浓茶”和“是否吸烟”对应的P值均小于0.001,有统计学意义。该结果在图25“参数估算值”中也同样可以体现。
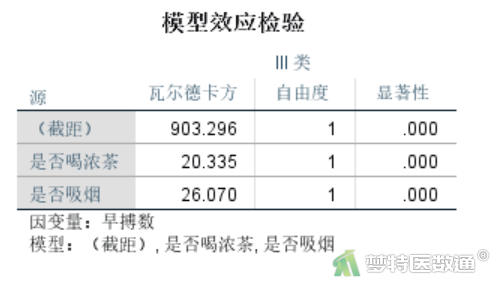
图25还展示了回归系数(β)和exp(β),后者即发生率比值(incidence-rate ratios,IRR,意同RR)。如果用Y表示早搏数,用X1表示是否喝浓茶,X2表示是否吸烟,可以得到模型的公式为:
Log(Y)=1.332+0.423*X1+0.608*X2
由图25可知,对于有胸闷症状的非器质性心脏病男性患者24小时早搏发生风险,喝浓茶者是不喝浓茶者的1.527倍(95%CI:1.270~1.835;P<0.001),吸烟者是不吸烟者的1.837倍(95%CI:1.455~2.321;P<0.001)。
四、结论
本研究采用Poisson回归探讨有胸闷症状的非器质性心脏病男性患者24小时早搏数的影响因素。观察变量早搏数为计数变量,且单位时间内其发生相互独立,经过软件判断服从Poisson分布,不存在需要处理的异常值,且自变量之间不存在严重共线性,数据满足Poisson回归分析的条件。
经过Poisson回归分析发现,Omnibus检验结果的似然比χ2值为32.884,P<0.001,说明纳入“是否喝浓茶”和“是否吸烟”的回归模型有统计学意义。对于有胸闷症状的非器质性心脏病男性患者24小时早搏发生风险,参数估计结果表明喝浓茶和吸烟都是导致早搏发生的危险因素,喝浓茶者是不喝浓茶者的1.527倍(95%CI:1.270~1.835;P<0.001),吸烟者是不吸烟者的1.837倍(95%CI:1.455~2.321;P<0.001)。
五、知识小贴士
(一) Poisson分布
人类稀有疾病或一些卫生事件,如恶性肿瘤、某地在一个月内因交通事故死亡人数、1ml水中大肠杆菌数等计数资料,具有发病率低或者不像二项分布资料有分母能计算比例等特点。因此,这些事件数的多少除了取决于事件的实际发生数,还取决于计数时研究者所观察的范围,即观察多长时间、多大人群、多大面积等。使用发病密度等密度指标描述这些事件的群体特征比较合适。对于此类罕见事件的发生,如果事件之间彼此相互独立,观察样本含量较大时,则具有平均计数等于方差的特点。这类事件的发生次数往往服从Poisson分布。
(二) Poisson回归
- Poisson回归主要用于单位时间、单位面积、单位空间内某事件发生数的影响因素分析。在进行稀有事件等计数资料的影响因素分析时,应首先对资料的过离散情况进行判断或检验分析,然后选择正确的回归模型分析,才能得到正确的结果。一般先从专业方面判断,然后用统计学方法检验资料是否存在过离散现象。如果资料存在过离散情况,选用负二项回归模型;如果资料无过离散情况,选用Poisson回归模型分析。Poisson回归和多重线性回归、Logistics回归、Cox比例风险模型、负二项回归等都是医学领域中应用最多的广义线性模型之一。
- SPSS中协方差矩阵下,“稳健估算量(Robust estimator)表示修正泊松回归法,其计算的效应量置信区间比“基于模型的估计量(Model-based estimator)更窄。本案例使用修正泊松回归计算结果为:喝浓茶者是不喝浓茶者的1.527倍(95%CI:1.206~1.933;P<0.001),吸烟者是不吸烟者的1.837倍(95%CI:1.397~2.416;P<0.001)。