主成分分析(Principal Component Analysis)——理论介绍

关键词：主成分分析；因子分析；降维；特征提取；数据简化

在实际工作或科研中，通常需收集众多变量以全面分析问题。然而，变量增多意味着需要更大的样本量和更复杂的模型，且可能引发变量间的严重多重共线性。为了充分有效地利用数据，人们希望用较少的新指标代替原来较多的旧变量，同时要求这些新指标尽可能地反映原始变量的信息。主成分分析和因子分析正是解决此类问题的有效方法，它们能够充分提取变量信息，减少分析变量个数，从而使问题更加简单直观，数据更加容易进行分析和处理。

举个简单例子，假设一个百万人的大型公司要对某项改革措施征询所有员工的意见，在传统的纸质函询时代，对每一个人都询问一遍显然太过费事，如果能对一部分具代表性的人进行询问，结果既具代表性又具高度可行性。在这个过程中有两个关键点：一是被询问的部分人群如何尽可能代表这百万人的意见，如果代表性不强，那么结果会存在较大偏差。二是被询问的人数如何尽可能的少，如果还要调查50万人，那么显然工作量并未显著降低，如果调查1万人，甚至1000人就可以，那实际操作性明显高多了！主成分分析的核心其实就体现在这个信息浓缩过程中，如何保障信息少丢失、又使提取的变量不要过多。

一、基本原理

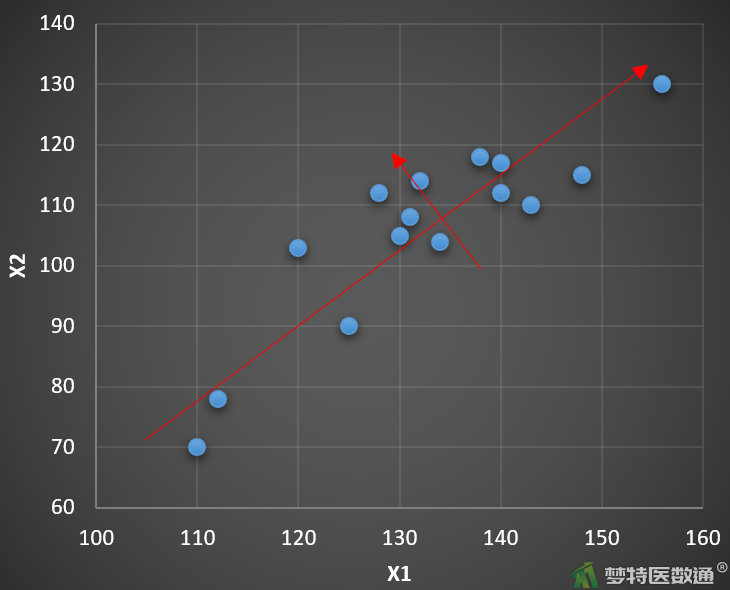
假设X1、X2两个变量之间存在高度共线性，用散点图表示其关系如图1所示。显然，两个变量之间存在明显相关性，如果直接将它们纳入模型，将难以避免多重共线性问题。要多这两个变量进行信息浓缩，其本质就是处理数据变异。在图中，散点构成了一个明显的椭圆形，该椭圆长轴方向上数据的变异明显大于短轴方向。沿着椭圆的长短轴方向设定一个新的坐标系，如图红线所示，则新产生的这两个变量和原始变量间存在着数学换算关系。但是这两个新变量彼此不相关，且信息量的分布显然不同：长轴方向上的变量携带了大部分数据的变异信息，而短轴方向上的变量只携带了一小部分变异信息。此时，只需使用长轴方向上的新变量，就可代表原先两个变量的大部分信息，从而达到了降维的目的。显然，两变量间的相关性越强，椭圆的长短轴就相差得越大，降维则越有价值。

二、模型结构

PCA的本质是设法将原来众多具有一定相关性的变量(如k个变量)，重新组合成一组新的相互无关的综合变量，以代替原来变量。通常数学上的处理是将原来k个变量作线性组合以产生新的综合变量。将选取的第一个综合变量记为F1，若方差var (F1)越大，表示F1包含的信息越多。因此在所有的线性组合中所选取的F1是方差最大的，故称之为第一主成分(PC1)。如果PC1不足以代表原来k个变量的信息，再考虑提取第二个线性组合F2，称为第二主成分(PC2)。依次类推，直到得到满意的信息浓缩。

假设有n个样本，测得k项指标(k＜n)，得到原始数据矩阵：X=(X₁，X₂，…，X_k)，且协方差矩阵为Σ，令协方差矩阵的特征值为λ₁≥λ₂≥…≥λ_k，所以有var (F1)≥var (F2)≥…≥var (F_k)≥0，向量Ι_1，Ι_2，…，Ι_k为相应单位特征向量，则X的第i个主成分为\(Z_{i}=I_{i}^{\mathrm{T}} X(i=1,2, \ldots, k)\)

实际情况下，协方差矩阵Σ往往未知，可以用其估计值S(样本协方差矩阵)来代替。同时由于指标的量纲不同，计算前往往要消除其影响，将原始数据做如下标准化：

\(S=R=\frac{1}{n} X^{T} X\)

因此也可以计算相关矩阵，从而得到特征值并进行PCA。原则上如果有n个变量，最多可以提取出n个主成分，试想如果提取的主成分数量k和变量n一样，那么也就失去了数据浓缩的价值。一般按累计贡献率去决定提取主成分的数量。

三、各统计量意义

(一) 特征值

特征值是衡量主成分解释力度的指标，它表示该主成分能解释的原始变量信息的平均量。如果特征值小于1，则说明该主成分的解释力度还不如直接引入一个原始变量的平均解释力度大。因此，一般可以用特征值大于1作为纳入标准。

(二) 主成分Z_i的方差贡献率

表明主成分Z_i的方差在全部方差中所占的比值。该值越大，表明主成分Z_i综合原始变量X₁，X₂，…，X_k的能力越强。计算公式为：\(\lambda_{i} / \sum_{i=1}^{k} \lambda_{i}\)

(三) 累积贡献率

指前k个主成分方差和在全部方差中所占的比值，常按照方差贡献率从大到小排列。一般来说，如果该指标达到85%，则表明这些主成分包含了全部测量指标所具有的的主要信息，这样既减少了变量的个数，又便于对实际问题进行分析和研究。但在医学研究中，大于70%也认为可以接受。

四、前提条件

开展PCA一般需要满足以下前提条件：

• 原始数据的变量数目较多，或有数据降维的需求，否则做主成分分析没有意义。
• 原始数据各个变量之间的共线性或相关关系较强，如果原始变量之间的线性相关程度很小，它们之间不存在简化的数据结构，这时进行主成分分析实际是没有意义的。
• 在应用PCA之前，需要对其适用性进行统计检验，检验方法有抽样适合性检验(measure sampling adequacy)和巴特利特(Bartlett)球形检验等。

五、分析步骤

PCA通常有以下4个步骤：

• 对于原来k个变量进行标准化，以消除变量在数量级或量纲上的影响。
• 根据标准化后的数据矩阵求出协方差或相关矩阵。
• 求出协方差或相关矩阵的特征值和特征向量。
• 确定主成分，在可能的情况下结合专业知识为各主成分赋予适当的专业解释。

六、主要用途

如前所属，这就可能产生各种各样的组和方法。主成分分析(Principal Component Analysis，PCA)是一种特征提取的方法。PCA主要用于解决信息浓缩问题，也可用于发现数据中的基本结构，即数据中变量之间的关系。PCA往往是大型研究中的中间环节，也用于其他机器学习方法的前处理。应用最典型的两种情况如下：

(一) 主成分评价

综合评价时，往往并非简单的求平均值可以解决，如评价某省份30个景区旅游竞争力，评价变量包括：年旅游人数(万人)、年景区住宿人数(万人)、人均住宿天数(天)、国内游客平均消费(元)、国际游客平均消费(元)、景区设施投资(万元)、景区工作人员数(人)、景区导游数(人)。不同变量的单位量纲并不一样，对其求平均值显然不科学。 在进行多指标综合评价时，由于要求评价结果客观、全面，就需要从各个方面用多个指标进行测量，但这样就使得被观测到的各指标间存在信息重叠，同时还会存在量纲差异、累加时如何确定权重等问题。此时就可以用PCA进行信息浓缩，并解决确定权重的问题。因此，主成分评价是对多个度量衡单位不同资料进行综合评价的一种重要方法。

(二) 主成分回归

在线性回归模型中，常用最小二乘法求回归系数的估计值。但是当存在多重共线性时，最小二乘法的估计结果并不理想，直接建立的多元线性回归方程具有不稳定性，严重时可导致正规方程组的系数矩阵为奇异矩阵，从而无法求得偏回归系数。若采用逐步回归，则不得不删除一些自变量，但这样就直接损失了删除变量的信息，与初衷相悖。将主成分分析与多元线性回归结合，即所谓的主成分回归，可以有效解决这一问题。通过这种方法，可以在减少变量个数的同时，保持模型的稳定性并避免信息的大量丢失。

具体做法是：首先，对多个自变量作主成分分析，综合出少数几个主成分。然后，使用这些主成分为自变量与因变量建立回归方程。这样既减少了回归分析中自变量的个数，而且作为自变量的各主成分互不相关，保证了回归方程的稳定性；同时，由于主成分是各原始变量的线性组合，因此通过主成分建立的回归方程实际上亦可视为因变量与各原始自变量之间的线性回归方程。这样就可把存在多元共线性的多个自变量引人回归方程。但主成分估计显然不是无偏估计，其核心目的是得到符合专业知识的回归系数估计值，而不是得到预测效果最好的回归方程。

七、优缺点

任何方法均具有相应的优缺点，总体而言PCA优缺点如下，在实际运用过程中能解决实际问题即可。

(一) 优点

• 仅仅需要以方差衡量信息量，不受数据集以外因素的影响。
• 各主成分之间正交，可消除原始数据成分间相互影响的因素。
• 计算方法简单，主要运算是特征值分解，易于实现。

(二) 缺点

• 主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。
• 方差小的非主成分也可能含有重要信息，因降维丢弃可能对后续数据处理有影响。